Zadanie1.2 Dla pręta zmiennym przekroju, obciążonego układem sił przedstawionych na rys.1.4a, obliczyć wartość sił i naprężeń normalnych w poszczególnych przekrojach, całkowitą zmianę długości oraz sporządzić wykresy sił i naprężeń normalnych.

Dane: F_i ,l_i , A_i , E. Do sporządzenia wykresów przyjąć : F₂ =3F₁ , F₃=5F_{1 ,} l₁ = l₂ =l₄ , l₃= 4l_1,

A₂=2A₁

Rozwiązanie: Korzystając ze wzorów (1.1) oraz (1.7) kolejno otrzymujemy:

N₁= -F₁ σ₁= -

N₂= -F₁ σ₂₌

N₃= -F₁ +F₂ σ₃₌

N4= -F1+F2-F3 σ₄₌

Granice przedziałów :

• punkty przyłożone siły

• miejsca zmiany przekrojów

Do obliczania zmiany długości wykorzystujemy zasadę superpozycji. Przy działaniu tylko siły F₁

∆l′= _-

• przy działaniu tylko siły F₂

∆l′′= _-

• przy działaniu siły tylko F₃

∆l′′′= _-

Całkowita zmiana długości wynosi

∆l= ∆lʹ +∆lʺ +∆lʹʹʹ

Po podstawieniu danych zależności między siłami oraz między długościami otrzymujemy

∆l=

Taki sam wynik otrzymujemy na innej drodze, omówionej w zadaniu 1.1. Obliczenie ∆l tą metodę pozostawiamy Czytelnikowi.

Wykresy sił i naprężeń normalnych przedstawiają rys. 1.4b i c.

Ponieważ w rozpatrywanym zadaniu wartości sił i naprężeń normalnych są różnego znaku, ich wartości odkładamy odpowiednio po lewej i po prawej stronie osi odniesienia 0-0.

Uwaga. Przyjęto, że odcinki podlegające ściskaniu są tak krótkie, że pręt nie ulega wyboczeniu. Obliczone wartości naprężeń występują w przekrojach dostatecznie odległych od miejsc przyłożenia siły (zasada de Saint-Venanta); nie uwzględniają także koncentracji naprężeń w miejscu zmiany przekroju (działanie karbu).

Zadanie 1.28 W układzie przedstawionym na rys. 1.28 pręta l został wykonany o δ za krótki. Obliczyć, jakie naprężenia powstaną w prętach po ich połączeniu z nieodkształcalną belką OB o ciężarze Q.

Dane: Q, l, δ, α, EA = const.

δ

Odpowiedź: Załóżmy, że po zmontowaniu układu i obciążeniu ciężarem Q oś belki zajmuje położenie OCʹBʹ . W tym przypadku warunek odkształceń ma postać

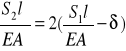
Po wykorzystaniu równań równowagi otrzymujemy

Przy stosunkowo małym ciężarze Q, σ₂ ˂ 0 , a oś belki zajmuje położenie OCʺBʺ. Otrzymane rozwiązanie jest słuszne, jeżeli nie ma niebezpieczeństwa wyboczenia pręta.

2. Rozwiązanie tego przypadku zostawia się Czytelnikowi.

A₂

F₃

l₄

l₃

l₂

l₁

F₂

A₁

F₁

1

1

2

2

3

3

4

4

Rys 1.4

a)

l, EA

δ

C

Cʺ

Cʹ

C₁

l, EA

Rys. .1.28

Bʹ

B

Bʺ

α

α

o

2

1

N

0

F₁

2F₁

0

3F₁

-

-

+

b)

δ

0

-

-

+

c)

Rys 1.4

---