Sprawozdanie z ćwiczenia nr 2.

Temat: Regulatory dwustanowe.

1. Wstęp teoretyczny.

W wykonywanym ćwiczeniu badaliśmy regulatory dwustanowe dlatego warto przytoczyć kilka podstawowych definicji związanych z wykonaniem ćwiczenia nr 2.

Sterowanie - celowe oddziaływanie na określony obiekt tak, by osiągnąć pożądany sygnał wyjściowy.

Sprzężenie zwrotne - występuje gdy w procesie dynamiczny polegającym na sterowaniu sygnał wyjściowy ma wpływ na sygnał wejściowy.

Regulacja - sterowanie w układzie zamkniętym posiadającym węzeł sumacyjny za pomocą którego realizowane jest ujemne sprzężenie zwrotne.

Regulator dwustanowy - to regulator o charakterystyce przekaźnikowej, którego wyjście może przybrać tylko dwie określone wartości. Stosuje się je tam, gdzie występuje ubytek sygnału wyjścia. Regulatory te służą do stabilizacji np. temperatury a ich działanie można śledzić na wykresach czasowych.

Stała czasowa inercji T - miara osiąganie stanu ustalonego przez sygnał wyjściowy związana z czasem trwania stanu nieustalonego.

Stała opóźniająca To - czas od momentu zmiany sygnału wejściowego do pojawienia się sygnału wyjściowego.

Histereza - właściwość regulatorów, której istota polega na tym, że zmiana stanu wyjściowego nie następuje w tym samym punkcie równym wartości zadanej ale do uaktywnienia wyjścia regulatora konieczny jest niewielki spadek wartości wyjściowej poniżej zadanej.

2. Przebieg ćwiczenia.

1. W pierwszej części ćwiczenia mieliśmy za zadanie analizę charakterystyk skokowych obiektu regulacji o transmitancji
   

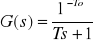
gdzie:

T - stała czasowa inercji

T₀ - stała opóźnienia.

Zarejestrowaliśmy, dla zadanych przez prowadzącego parametrów, przebiegi odpowiedzi obiektu, które są przedstawione na wykresie numer 3.1.2.3.4.

Zadane parametry:

L.p.	T	T0
1.	4	0,5
2.	4	0,75
3.	2	0,75
4.	2	0

2. W drugiej fazie ćwiczenia mieliśmy za zadanie zarejestrować przebiegi regulacji sygnałów wejściowych i wyjściowych dla zadanych przez prowadzącego parametrów.

Parametry, które ulegały zmianie to strefa histerezy (N) i współczynnik proporcjonalności x_p. Wykresy są przedstawione kolejno na załączonych kartach 4.1, 4.2, 4.3, 4.4.

Zadane parametry:

L.p.	N	xp
1.	0	0
2.	10	0
3.	0	3
4.	10	3

3. Wnioski

Analizując wykres 3.1.2.3.4 (wykres został wykonany własnoręczne, gdyż wykres oryginalny uległ zniszczeniu) widać wyraźnie, że stała opóźnienia ma znaczący wpływ na przebieg sygnału wyjściowego. Widać, że im większa stała opóźnienia (porównując przebieg nr 1 i 2), tym opóźnienie w czasie rozpoczęcia pracy obiektu jest większe. W rzeczywistości stała opóźnienia wpływa na zmniejszenie stabilności układu i powstaje w wyniku przetwarzania sygnału.

Gdy porównamy przebiegi nr 2 i 3 zauważymy bezpośredni wpływ stałej czasowej inercji na przebieg odpowiedzi obiektu. Dla przebiegu 3 i 4 lub 1 i 2 czas trwania stanu nieustalonego był taki sam. Widać, że stała czasowa wpływa na czas osiągnięcia przez układ stanu ustalonego. Obiekt regulacji osiąga stan ustalony gdy wartość uchybu nie zmienia się. Na wykresie ilustruję to linia pozioma.

Obserwując wykres, które obrazują sygnał sterujący i wyjścia przy ustalonym, stałym współczynniku proporcjonalności i zmianie strefy histerezy zauważamy, że amplituda rośnie a częstotliwość maleje wraz ze wzrostem strefy histerezy. Porównując wykresy gdzie występuję stała strefa histerezy a zmienny jest współczynnik proporcjonalności widzimy, że im większy współczynnik proporcjonalności tym amplituda jest mniejsza, ale zwiększa się częstotliwość. Dokładność regulacji mierzy się amplitudą, która zależy od szerokości pętli histerezy. Aby poprawić regulację należy dążyć do zmniejszenia amplitudy. Widzimy również, jak wpływa włączenie i wyłączenie elementu dwustawnego. Kiedy charakterystyka sygnału sterującego przechodzi przez górną część strefy histerezy element zostaje włączony, natomiast, gdy charakterystyka przechodzi strefę od dołu element zostaje włączony. Na każdym wykresie wyraźnie widać stałą opóźnienia. Widoczne jest również to, że element nie przeskakuję dokładnie w punkcie przekroczenia charakterystyki u w granicach stery histerezy.

---