1. Krótki opis metody pomiaru

Pomiar prędkości dźwięku w powietrzu zrealizować można w układzie przedstawionym poniżej:

Podaliśmy sygnał sinusoidalnie zmienny z generatora na głośnik i obserwując ekran oscyloskopu mierzyliśmy takie położenie głośnika względem mikrofonu, aby uzyskać obraz figury Lissajous (w naszym przypadku skośne linie). Wyniki zapisaliśmy w tabeli.

2. Tabela

Sygnał z generatora		Numer pomiaru	Położenie mikrofonu	Dystans	c+Δc
f[Hz]	Δf[Hz]	i	ri[m]	D=ri+1-ri[m]	[m/s]
3500	100	1	0,395	0,058
				2		0,337	0,051
				3		0,286	0,065
				4		0,221	0,061
				5		0,160	0,060
				6		0,220	0,067
				7		0,287	0,053
				8		0,340	0,055
				9		0,395	-
		3700	100	1		0,369	0,047
				2		0,322	0,059
				3		0,263	0,062
				4		0,201	0,051
				5		0,150	0,050
				6		0,200	0,059
				7		0,259	0,059
				8		0,318	0,048
				9		0,368	-

3. Obliczenia i rachunek błędów

1. obliczanie średniej arytmetycznej pomiarów D_śr:

D_{śr 3500} = 0,06 m

D_{śr 3700} = 0,05 m

2. średni błąd kwadratowy serii pomiarów ΔD obliczamy ze wzoru:

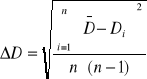
ΔD₃₅₀₀ = 0,002

ΔD₃₇₀₀ = 0,002

3. błąd pomiaru ΔD_α stosując metodę Studenta z założonym poziomem ufności α=0.95 dla dziewięciu pomiarów (t = 2,896) wynosi:

ΔD_α=t_α*ΔD.

Dla 3500Hz ΔD_{α 3500} = 0,005

Dla 3700Hz ΔD_{α 3700} = 0,005

4. prędkość fali akustycznej w powietrzu obliczam ze wzoru:

c = 2f ⋅ D_śr

Dla 3500Hz c₃₅₀₀ = 406 m/s

Dla 3700Hz c₃₇₀₀ = 400 m/s

5. błąd całkowity pomiaru obliczam ze wzoru:

Δc = 4⋅[ D_śr⋅Δf + f⋅ΔD_α]

Dla 3500Hz Δc₃₅₀₀ = 74

Dla 3700Hz Δc₃₇₀₀ = 82

6. ostateczny wynik pomiaru to:

Dla 3500Hz c₃₅₀₀ = 406 ± 74 m/s

Dla 3700Hz c₃₇₀₀ = 400 ± 82 m/s

Powyższe wyniki umieściliśmy w tabeli pomiarowej.

4. Dyskusja wyników

Wyniki otrzymane w powyższym doświadczeniu odbiegają od wartości rzeczywistych, jednak mięszczą się w granicach błędu. Przyczynami które doprowadziły do różnic między wartościami pomiarów a wartościami realnymi były:

- hałas wokół stanowiska pomiarowego

- mała dokładność na ławie z podziałką liniową

• błąd odczytu na oscyloskopie

• mała czułość oscyloskopu.

3

Oscyloskop

Generator

akustyczny

Mikrofon

Głośnik

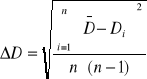
Ława z podziałką

---