POLITECHNIKA ŚLĄSKA
Wydział Automatyki, Elektroniki
i Informatyki
AUTOMATYKA I ROBOTYKA
Laboratorium z FIZYKI
ĆWICZENIE NUMER 10
Dyfrakcja światła: wyznaczanie stałej siatki dyfrakcyjnej, pomiar długości światła laserowego, wyznaczanie szerokości szczeliny.
GRUPA IV
SEKCJA NR 12
Tomasz Hałat
Paweł Jasiaczek
Gliwice 1999.05.14.
1. Opis zjawiska:
Dyfrakcja jest to zjawisko fizyczne polegające na ugięciu fali elektromagnetycznej na ostrych krawędziach przedmiotów lub wąskich szczelinach o rozmiarach porównywalnych z długością tej fali. Istnieją dwa rodzaje dyfrakcji: gdy ekran i źródło światła znajdują się na tyle daleko, że promienie padające na szczelinę i promienie padające na ekran są równoległe, to wówczas mówimy o dyfrakcji Fraunhofera. W przeciwnym przypadku występuje dyfrakcja Fresnela. Dyfrakcji dotyczy również zasada Huygensa , która mówi , że każdy punkt do którego dochodzi fala staje się źródłem nowej fali kulistej. Zasadę tę uzupełnił Fresnel twierdząc, że każdy element powierzchni falowej jest źródłem kulistej fali wtórnej, której amplituda jest proporcjonalna do wielkości tego elementu. Światło monochromatyczne uginając się na szczelinie powoduje powstanie na ekranie, który znajduje się za szczeliną, prążków jasnych i ciemnych. Spowodowane to jest interferencją załamanych fal za szczelinie. Pasek centralny za szczeliną może być jasny lub ciemny, zależy to od odległości ekranu od szczeliny.
Warunek na wzmocnienie fali :
![]()
![]()
Warunek na wygaszenie fali :
![]()
gdzie: k=1,2,3,... ; λ - długość fali; d - szerokość szczelin.
Siatka dyfrakcyjna to płytka szklana z szeregiem szczelin umieszczonych w równych odległościach od siebie. Siatka dyfrakcyjna posiada swoją stałą, która jest wyrażona poprzez odległość między środkami sąsiednich szczelin. Jeżeli siatkę dyfrakcyjną oświetlimy wiązką równoległych promieni to na siatce wystąpi dyfrakcja. Światło ugnie się na każdej szczelinie, co spowoduje powstanie na ekranie maksimów i minimów. Na ekranie uzyskujemy maksima gdy zachodzi następująca równość:
![]()
Natomiast minima przy równości :
![]()
gdzie: d - stała siatki; N - liczba szczelin; k=1,2,3... ; λ - długość fali.
Pomiędzy maksimami występuje N-1 minimów oraz N-2 maksimów wtórnych , w których natężenie jest bardzo małe. Światło monochromatyczne wykorzystujemy do badania zjawiska dyfrakcji. W tym celu wykorzystujemy światło laserowe. Laser jest to urządzenie, którego zasada działania opiera się na teorii promieniowania wymuszonego Einsteina. Polega ona na tym, że kwant energii równej hν pada na wzbudzony atom, powoduje to wypromieniowanie dodatkowego kwantu energii, który jest spójny z kwantem wywołującym emisję światła laserowego. Do uzyskania wzbudzonych atomów stosuje się proces pompowania optycznego.
2. Opis przebiegu ćwiczenia:
W pierwszej części ćwiczenia naszym zadaniem jest wyznaczenie stałej siatki dyfrakcyjnej. Na podstawie wyników pomiarów stałej siatki możemy wyznaczyć w następnej części ćwiczenia długość światła laserowego przepuszczając je przez tą samą siatkę. Natomiast znajomość długości fali pozwala wyznaczyć szerokość szczeliny, przez którą w trzeciej części ćwiczenia przechodzi promień światła lasera. Stałą siatki dyfrakcyjnej wyznaczamy za pomocą spektrometru (odczytując kąty ugięcia dla trzech kolejnych prążków z lewej i prawej strony). Następnie, dla tej samej siatki, odczytujemy odległości pomiędzy kolejnymi prążkami światła lasera przechodzącego przez siatkę i padającego na wyskalowany ekran. W tym czasie wyznaczana jest zależność natężenia prądu od odległości od prążka głównego, na podstawie której wyznaczyliśmy szerokość szczeliny.
Karta pomiarowa:
4. Wykres zależności natężenia prądu w fotorezystorze od odległości od
Opracowanie wyników pomiarów:
5.1. Wyznaczanie stałej siatki dyfrakcyjnej.
Stałą siatki dyfrakcyjnej wyznaczamy z następujących wzorów:
![]()
![]()
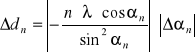
gdzie: d - stała siatki dyfrakcyjnej, n - rząd prążka dyfrakcyjnego, ∝n - kąt ugięcia dla n rzędu, - długość światła, w tym przypadku = 589,3 [nm]
Błąd odczytu kąta wyznaczamy metodą rozstępu z próby:
![]()
|
n = 1 |
n = 2 |
N = 3 |
|||
αśr |
184°24' |
171°56' |
191°20' |
165°04' |
198°20' |
158°16' |
Δα |
16' |
16' |
0' |
26' |
0' |
16' |
Błąd wyznaczamy ze średniej arytmetycznej
1 = (6°14' ± 16')
2 = (13°08' ± 13')
3 = (20°02' ± 8')
d1 = 5,43⋅10-6[m] Δd1 = 0,16⋅10-6[m] n = 1
d2 = 5,19⋅10-6[m] Δd2 = 0,13⋅10-6[m] n = 2
d3 = 5,16⋅10-6[m] Δd3 = 0,08⋅10-6[m] n = 3
Stałą siatki dyfrakcyjnej wyznaczamy ze wzoru na średnią ważoną:
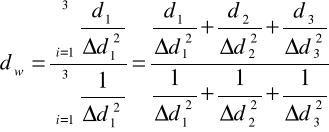
a jej błąd ze wzoru:
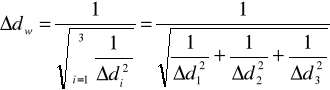
Ostatecznie otrzymujemy:
d = (5,21⋅10-6 ± 0, 07⋅10-6 ) [m]
5.2. Wyznaczanie długości światła lasera.
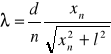
![]()
gdzie: - długość światła lasera, xn - odległość prążka rzędu n-tego od prążka rzędu 0 (środkowego), l - odległość szczeliny od ekranu.
Δl - 5⋅10-4 [m] - błąd odczytu odległości od siatki do ekranu
Δx - 5⋅10-4 [m] - błąd odczytu odległości na ekranie
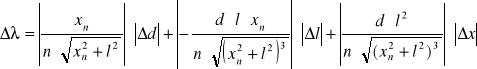
[m]
1 = 6,93⋅10-7 [m] Δ1=0,04⋅10-7 [m]
2 = 6,95⋅10-7 [m] Δ2=0,05⋅10-7 [m]
3 = 6,95⋅10-7 [m] Δ3=0,06⋅10-7 [m]
Korzystając ze wzoru na średnią ważoną wyliczamy λ i jej błąd. Ostatecznie otrzymujemy więc:
= 694 ± 3 [nm]
5.3. Wyznaczanie szerokości szczeliny.
Szerokość szczeliny wyznaczamy ze wzoru:
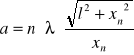
gdzie: a - szerokość szczeliny, n - numer kolejnego maksimum, - długość fali świetlnej lasera, l - odległość szczeliny od fotorezystora, xn - odległość n- tego ciemnego prążka od jasnego prążka centralnego .
Δl = 5⋅10-4 [m]
Δxn = 5⋅10-4 [m]
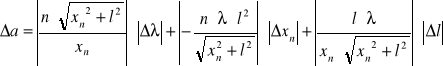
a1=8,40⋅10-5 [m] Δa1 = 0,08⋅10-5 [m] xn1 = 4,13⋅10-3 [m]
a2=8,41⋅10-5 [m] Δa2 = 0,04⋅10-5 [m] xn2 = 8,25⋅10-3 [m]
Ostatecznie otrzymujemy więc:
a = 8,41⋅10-5 ± 0,04⋅10-5 [m]
6. Podsumowanie:
Ostatecznie otrzymaliśmy następujące wyniki wyznaczanych wartości:
d = ( 5,21⋅10-6 ± 0,07⋅10-6 ) [m] (stała siatki dyfrakcyjnej);
λ = (694 ± 3) [nm] (długość fali światła lasera);
a = (8,41⋅10-5 ± 0,04⋅10-5 ) [m] (szerokość szczeliny).
W doświadczeniu obserwowaliśmy zjawisko dyfrakcji światła, które zachodzi jedynie w wypadku napotkania przez falę świetlną na przeszkodę o porównywalnych rozmiarach z długością tej fali. Otrzymane w ćwiczeniu wyniki mają wartości różniące się niewiele. Pomimo to zjawisko dyfrakcji zachodzi (im większa szerokość szczeliny tym kąt odchylenia się fali świetlnej jest mniejszy).
.
![]()
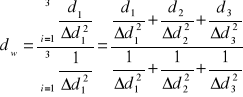
![]()
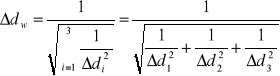
Wyszukiwarka
Podobne podstrony:
Dyfrakcja światła 1 , POLITECHNIKA ŚLĄSKA
Dyfrakcja, Dyfrmoje, Politechnika Śląska
Dyfrakcja światła 5 , Politechnika ?l?ska
dyfrakcja światła, Politechnika
DYFRAKCJA SWIATLA, Politechnika ˙l˙ska Gliwice 3.03.1997
Laboratorium 7 - Wyznaczanie współczynnika załamania światła w powietrzu (2), Politechnika Śląska
Laboratorium 7 - Wyznaczanie współczynnika załamania światła w powietrzu (2), Politechnika Śląska
Sprawozdanie - dyfrakcja, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BU
Dyfrakcja, SPR-DYFR1, Politechnika Śląska Studia Wieczorowe
Laboratorium 7 - Wyznaczanie współczynnika załamania światła w powietrzu (3), Politechnika Śląska w
KARTA INSTRUKCYJNA OBROBKI2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Se
17 listopada, Politechnika Śląska semestr I GiG, Górnictwo
wzory Finanase przedsiebiorstw, Politechnika Śląska ZiIP i inne, Finanse
czystakartainstrukcyjnaobrobki, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL,
Rozk ad labów, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Inżynierskie, Se
Politechnika Śląska sprawko moje (Naprawiony)
Politechnika śląska w gliwicach sprawko na dziekana
podstawowe informacje o ochronie prawnej wzorów przemysłowych, Studia - Politechnika Śląska, Zarządz
więcej podobnych podstron