Ćwiczenia statyka 2 - 6 -
Zadanie 7
Na rysunku 7 przedstawiono dwa ciała o danych ciężarach G1 i G2 zawieszone na trzech cięgnach. Cięgno AB w położeniu równowagi tworzy z osią x kąt αAB. Określić wartość liczbową kąta α2 jeśli G1 = 12N, G2 = 21N, α1 = 350, αAB = 50.
y
C α2 D
α1
αAB
B
A x
G1 G2
Rys.7
Rozwiązanie
Równowaga węzła A (rys.7a)
αS1 = 900 + α1, αG1 = 2700, αAB = 50
y
S1 αS1
SAB
αAB
A x
αG1
G1 Rys.7a
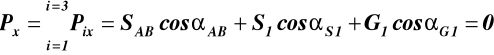
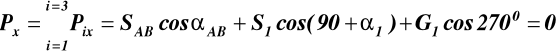
![]()
, ![]()
(1)
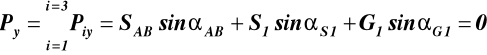
![]()
![]()
(2)
Z (1) określamy S1 i wstawiamy do (2) - 7 -
![]()
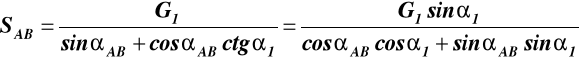
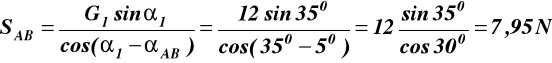
(3)
Równowaga węzła B (rys.7b)
y S2
αBA = αAB +1800
αBA αG2 αS2 = (900 - α2), αG2 = 2700
x
B
SBA
G2 Rys.7b
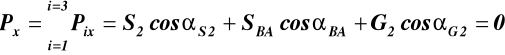
![]()
![]()
(4)
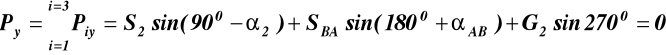
![]()
(5)
Równowaga cięgna AB (rys.7c)
- SBA
B
- SAB A Rys.7c SAB = SBA
Podstawiając (3) do (4) otrzymujemy 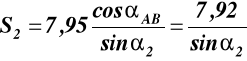
(6)
Podstawiając (3) i (6) do (5) otrzymujemy 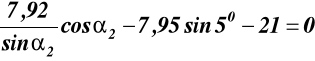
stąd tgα2 = 0365 α2 = 200
z (1) S1 = 13,80N,
z (6) S2 = 23,15N
Zadanie 8 - 8 -
Ciało o ciężarze G = 100N zawieszono na wsporniku składającym się z trzech prętów połączonych przegubowo w sposób podany na rysunku 8. Pręty 0A i 0B leża w płaszczyźnie prostopadłej do pionowej ściany π, tworzą z tą ścianą kąty δ1 = 500 i δ2 = 550. Pręt 0C tworzy z pionową ścianą kąt δ3 = 460 i również leży w płaszczyźnie prostopadłej do tej ściany. Obliczyć siły w prętach, pomijając ich ciężary własne oraz tarcie w przegubach.
z
π B
D δ2
δ1 0
A y
δ3
x
G
C
Rys.8
Rozwiązanie
Na rysunku 8a przedstawiono siły oddziaływania prętów na węzeł 0
z
B
S0Cxy=S0Cy
δ2 0
S0B
δ1 S0A 0 S0C S0Cz
A
y
S0C
δ3
x
G
C Rys.8a
Składowe sił działających w płaszczyznach 0xy (rys.8b) i 0yz (rys.8c) na węzeł 0.
B Na rysunku 8b pokazano kąty
S0B jakie tworzą te składowe z osią x.
δ2 αS0A = 3600-δ1 Na rysunku 8c pokazano kąty
S0Cxy 0 y między składowymi sił a osią z.
δ1
S0A αS0Cxy = 2700
A x αS0B =1800+δ2 Rys.8b
9 -
Warunki równowagi na osie x i y
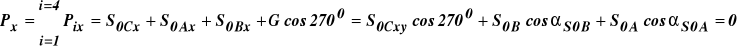
![]()
![]()
(7)
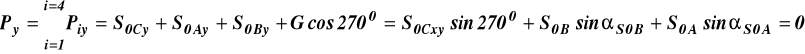
![]()
![]()
![]()
![]()
(8)
Warunek równowagi na oś z
z
γS0C γS0C = 1800 - δ3
S0Ay 900 S0By
y
D 0
S0C G
δ3
C Rys.8c
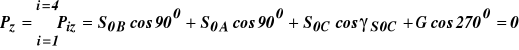
![]()
![]()
(9)
Wstawiamy (9) i (7) do (8) oraz z (7)
![]()
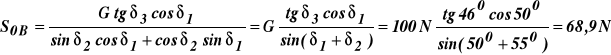
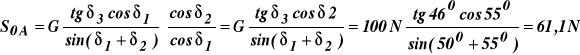
Wyszukiwarka
Podobne podstrony:
Mechanika - Statyka, cwiczeniastatyka3, Ćwiczenia statyka 3
Mechanika - Statyka, cwiczeniastatyka4, Ćwiczenia statyka 4
Mechanika gruntów Ćwiczenie 5 Sprawozdanie 3
Mechanika gruntów - Ćwiczenie 1 - Sprawozdanie 1, Budownictwo S1, Semestr III, Mechanika gruntów, La
Mechanika statyka teoria
Mechanika gruntów - Ćwiczenie 5 - Sprawozdanie 4, Budownictwo S1, Semestr III, Mechanika gruntów, La
podst mechaniki plynow cwiczenia
Symulacja E ogarnijtemat.com, SiMR inżynierskie, Semestr 4, Laboratorium Mechaniki Płynów, Ćwiczenia
sprawko przeplyw nasze ogarnijtemat.com, SiMR inżynierskie, Semestr 4, Laboratorium Mechaniki Płynów
Mechanika - Dynamika, cwiczeniadynamika12, Cwiczeniadynamika11
mechanika, 14+, Ćwiczenie 15
Mechanika gruntów Ćwiczenie 1 Sprawozdanie 2
Mechanika płynów ćwiczenia
Mechanika gruntów Ćwiczenie 4 Sprawozdanie
Mechanika - Statyka, statykawyklad6, Środek ciężkości
mechanika budowli ćwiczenia (11 04 2010 r )
Mechanika gruntów - Ćwiczenie 2 - Sprawozdanie, Budownictwo S1, Semestr III, Mechanika gruntów, Labo
Mechanika - Statyka, statykawyklad1, Statyka Wykład 1
Mechanika - Dynamika, cwiczeniadynamika10, Ćwiczenia 10
więcej podobnych podstron