Statyka Wykład 1
Literatura: Mechanika Techniczna tom 1 Jan Misiak
Rozróżniamy następujące siły:
_- masowe lub objętościowe
powierzchniowe
zewnętrznewewnętrzne
Jednostką siły w układzie międzynarodowym SI jest
![]()
Zasady statyki:
Zasada pierwsza. Działanie dwóch sił P1 i P2 można zastąpić działaniem jednej siły R (rys.1), której wartość liczbowa
P1
α R
P2 Rys.1
wynosi: ![]()
(1)
Zasada druga. Jeśli do ciała przyłożone są dwie siły, to równoważą
się one tylko wtedy , kiedy mają tę samą linię działania, te same
wartości liczbowe i przeciwne zwroty (rys.2)
P1 = -P2 P1 = P2
P1 P2
l
Rys.2
Zasada trzecia. Skutek działania dowolnego układu sił, przyłożonego do ciała nie zmieni się, jeśli do tego układu dodamy
lub odejmiemy dowolny układ równoważących się sił P2 i -P2 czyli
tzw. układ zerowy (rys.3)
P1
B
-P2 A P2
l Rys.3
St.2
Zasada czwarta (zasada zesztywnienia).
Jeżeli ciało odkształcone znajduje się w równowadze pod działaniem pewnego układu sił, to również pozostanie w równowadze ciało doskonale sztywne (nieodkształcalne) identyczne z poprzednim, pod działaniem tego samego układu sił.
Zasada piąta ( zasada działania i przeciwdziałania).
Każdemu działaniu towarzyszy równe co do wartości o przeciwnym zwrocie i leżące na tej samej prostej przeciwdziałanie
B R R
B B R
A
A A
O A
G 0 -R
G G
Rys.4 G = - R
Zasada szósta (zasada oswobodzenia od więzów)
Każde ciało można oswobodzić z więzów, zastępując ich działanie
reakcjami, a następnie rozpatrując jako ciało swobodne, znajdujące się pod działaniem sił czynnych i biernych (reakcji więzów)
A B
R1 R2
C
G G
Rys.5
Pojęcie skalara i wektora St.3
B l
a
A
Rys.6 a = AB
Moduł wektora a = AB = a
Rozróżniamy trzy rodzaje wektorów:
- wektory związane z punktem ( wektory uczepione)
z
a M(x,y,z)
0 r
0 y
x
Rys.7 r - promień wektor
wektory związane z prostą (wektory ślizgające się, wektory
posuwne)
l
a
a
a
Rys.8
- wersor (wektor jednostkowy)
a0 a0 = a0 = 1 Rys.9
- wersory zwiazane z osiami układu prostokątnego
z
k
j y
i 0
x Rys.10
Składowe wektora a w układzie kartezjańskim St 4
z z
az az
a γ a
k β
0 j ay y ay y
i ax α
ax
x x
Rys.11
Wartość modułu wektora a 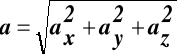
(2)
cosinusy kątów 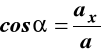
, 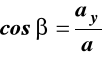
, 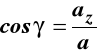
(3)
Dodawanie wektorów
a a
b c
b
a + b = c
Rys.12
Mnożenie wektorów - iloczyn skalarny i wektorowy
a
0 β ![]()
(4)
b
a ![]()
(5)
α
![]()
(6)
900 900 b
c Rys.13
Analityczne wyrażenie iloczynu skalarnego wektorów a i b St5
![]()
(7)
ponieważ ![]()
patrz (4)
oraz ![]()
stąd (8)
![]()
(9)
Analityczne wyrażenie iloczynu wektorowego dwóch wektorów
![]()
![]()
(10)
ponieważ ![]()
patrz (6)
![]()
, ![]()
, ![]()
patrz (5)
![]()
, ![]()
, ![]()
(11)
stąd wyrażenie (10) jest rozwinięciem wyznacznika
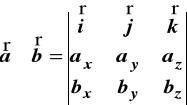
(12)
Przykład 1
Dane są wektory ![]()
, ![]()
Obliczyć:
a) sumę wektorów ![]()
b) kąt między tymi wektorami αab
c) wartości kąów α,β,γ jakie wektor c tworzy z osiami
współrzędnych 0xyz
d) wartość iloczynu skalarnego wektorów a i b
e) iloczyn wektorowy, wektorów ![]()
f) wartość wektora d
Rozwiązanie
ad a) ![]()
![]()
(a)
ad b) z (4) 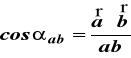
St.6
z (9) ![]()
z (2) ![]()
![]()
ostatecznie ![]()
![]()
ad c) z (3) 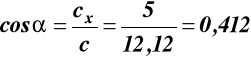
![]()
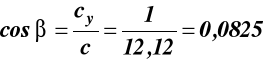
![]()
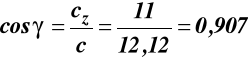
![]()
ad d) iloczyn ten obliczono w punkcie b)
![]()
ad e) z (12)
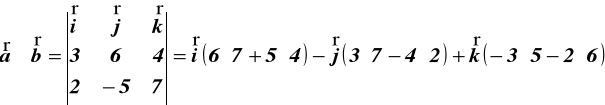
![]()
ad f) z (2) ![]()
St 1
Wyszukiwarka
Podobne podstrony:
Mechanika - Statyka, statykawyklad2, Statyka Wykład 2
Szkic do wykladow z mechaniki statyka
Mechanika Teoretyczna Statyka Wykład
Mechanika - Statyka, statykawyklad4, Statyka Wykład 4
Szkic do wykladow z mechaniki statyka
Mechanika statyka teoria
Mechanika - Statyka, statykawyklad6, Środek ciężkości
Mechanika - Statyka, cwiczeniastatyka3, Ćwiczenia statyka 3
Mechanika - Statyka, cwiczeniastatyka2, Ćwiczenie statyka 2
Mechanika - Statyka, cwiczeniastatyka4, Ćwiczenia statyka 4
Mechanika statyka teoria
Mechanika płynów na kolosa z wykładów
Mechanika Budowli Sem[1][1] VI Wyklad 04
Statyka - Przestrzenny Układ Sił, sem II, Mechanika Techniczna I - Wykład.Ćwiczenia, Zestaw V (oce)
Obliczenia + gwinty, IŚ Tokarzewski 27.06.2016, V semestr COWiG, PKM (Podstawy konstrukcji mechanicz
Mechanika Budowli Sem[1][1] VI Wyklad 02 color
notatek pl budowa mechanizm wsalania i wysalania bialek wyklad
więcej podobnych podstron