Statyka Wykład 4 St.20

Równowaga dowolnego płaskiego układu sił

Z równań (35), (36)

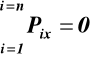
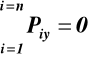
(37)

lub pod warunkiem że punkty A,B i C nie leżą na jednej prostej

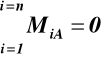
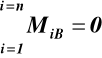
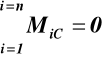
(38)

Przykład 8

Nieważka belka AB = 3l jest zamocowana w punkcie A na stałej podporze przegubowej, a w punkcie B na podporze przegubowej przesuwnej (rys.31). Obciążenie belki stanowią siły P₁ = 251N

i P₂ = 283N, a kąt α = 26,5⁰. Obliczyć reakcje w punktach podparcia A i B.

y P₂

A B α

x

l P₁ l l

Rys.31

Rozwiązanie

y

R_B P₂

R_Ay α_RAy α_P1 α_RB α_P2

A R_Ax B x

l P₁ l l

Rys.32

Warunki równowagi (37)

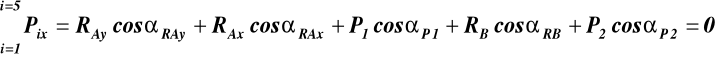
(a)

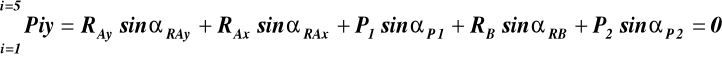
(b)

gdzie: α_RAx = 0, α_RAy = 90⁰, α_P1 =270⁰, α_RB = 90⁰, α_P2 = 180⁰ - α

Równanie momentów względem A (rys.33) St.21

*_P1 = 270⁰

R_Ay

R_Ax r_Ax = r_Ay = 0 r_P1

A A

P₁ r_P1 = l = h_P1

R_B

*_RB = 90⁰

r_RB r_RB = 2l = h_RB

A B

90⁰

h_P2

P₂ *_P2 = 180⁰ - α

α

A r_P2 r_P2 = 3l

Rys.33

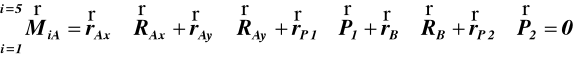
(c)

z (c)

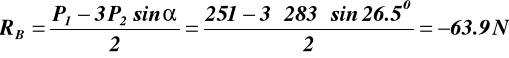
z (a)

stąd

z (b)

stąd

Reakcja podpory A na belkę

Reakcja podpory B na belkę R_B = - 63.9N

Tarcie ślizgowe St.22

Doświadczenie Coulomba

y

N

R α Dla początku ruch α = ρ

wtedy T = T_g (graniczne)

T P oraz P = P_max

0 x

G Rys.34

(d)

Stąd

T = P N = G (39)

Zależność między siłą tarcia T a działającą siłą P (rys.35)

T

B

T_g

C

45⁰

0 D P Rys.35

0B zakres tarcia ślizgowego statycznego

BC zmiana tarcia ślizgowego kinetycznego

D początek ruchu

Z rys. 34 T = Ntgα T_g = Ntgρ =Nk gdzie 0 ≤ k ≤ μ jeśli tgρ = μ to

μ^' T_g = μN (40)

μ

V Rys.36 Zależność

kinetycznego współczynnika tarcia od prędkości względnej ciała V

T^' = μ^'N (41)

St.23

Materiał	^Współczynnik tarcia ślizgowego
		^statycznego μ	kinetycznego μ^'
żeliwo po żeliwie	^0,22	^0,1
kamień po kamieniu	^0.6^÷^0.7	^-----------------
Stal po lodzie	^0.03	^0.015

Przykład 9

Ciało o masie m = 92kg spoczywa na podłożu (rys.37), należy określić, pod jakim kątem α do poziomu powinno być nachylone

cięgno, za które ciągnie się dane ciało, aby siła P potrzebna do

wywołania poślizgu osiągała wartość minimalną. Współczynnik tarcia równy jest μ = 0.22, g = 9.81m/s².

y P

α

G

0 N

x

T Rys.37

Rozwiązanie

G = mg = 92kg9.81m/s² = 902.5N

Na rysunku 38 przedstawiono kąty między osią x i wektorami sił

α_G = 270⁰ P α_P = α

x x

G α_T =180⁰ N

α_N = 90⁰

x x

Rys.38 T

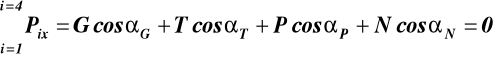
(e)

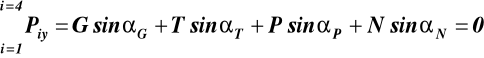
(f)

Po podstawieniu wartości kątów do równań (e) i (f)

z (e)

St.24

z (f)

Na granicy równowagi

stąd

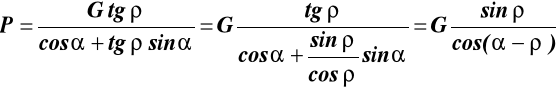
Jeśli jest poślizg to P >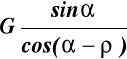

P_min gdy
α = ρ, tgρ = 0.22

ρ = α= 12.4⁰

Minimalna siła potrzebna do przesunięcia ciała P_min >Gsinα

P_min > 902.5sin12.4⁰ = 193.8N

---