Politechnika Krakowska Fizyka Techniczna	Paweł Górski	Rok akad.: 1999/2000		Data: 19.10.1999
Grupa 1 Zespół 7		Nr ćwicz.: 25	Ocena:		Podpis:

Temat:

Badanie pola ma pomocą hallotronu.

Podczas badań nad naturą sił działających na nośniki prądu w polu magnetycznym E. H. Hall odkrył ciekawy efekt nazwany później jego imieniem. Polega on na tym, że jeżeli przewodnik, w którym płynie prąd umieścimy w polu magnetycznym prostopadłym do kierunku prądu, wewnątrz przewodnika oprócz „zwykłego” pola elektrycznego powstaje pole elektryczne prostopadłe do kierunku prądu jak i do kierunku pola magnetycznego.

Pole to można wykryć mierząc napięcie między punktami P₁ i P₂. Punkty te są tak dobrane, że w nieobecności pola magnetycznego różnica potencjałów między nimi jest równa zeru. Gdy włączymy teraz pole magnetyczne, pojawi się miedzy nimi napięcie zwane napięciem Halla.

Przyjmijmy, że nośniki prądu w próbce przewodzącej (elektrony), można uważać za swobodne. Przed włączeniem pola magnetycznego poruszają się one ze średnią prędkością unoszenia
w kierunku przeciwnym do pola elektrycznego
. Po włączeniu pola magnetycznego na nośniki prądu będzie działać siła Lorentza o wartości:

skierowana prostopadle do ich prędkości
i do wektora indukcji
. Wskutek czego na jednym z boków próbki wytworzy się nadmiar elektronów i bok ten naładuje się ujemnie, a na przeciwnym boku pozostaną jony dodatnie. Powstanie pole elektryczne
prostopadłe do kierunku przepływu prądu, a zatem pojawi się siła elektrostatyczna
skierowana przeciwnie do kierunku działania siły Lorentza. W warunkach równowagi siły Lorentza i siły elektrostatycznej zachodzi równość:

a stąd:

Pole elektryczne
jest związane z napięciem Halla
w następujący sposób:

Z definicji natężenia prądu:

gdzie: n - ilość nośników w jednostce objętości próbki

S - pole powierzchni przekroju próbki

W naszym przypadku
, zatem

stąd:

Stała
jest nazywana stałą Halla, a jej znak zależy od znaku nośników prądu. W przypadku elektronów
, co daje
. Dla niektórych materiałów otrzymujemy jednak dodatnią wartość
i mówimy wtedy o anomalnym efekcie Halla. Tłumaczymy go obecnością w próbce dodatnich nośników prądu - dziur.

Efekt Halla jest podstawą działania elementu elektronicznego zwanego hallotronem. Wykorzystuje się je przede wszystkim do wykrywania pola magnetycznego i pomiaru indukcji magnetycznej.

Parametrem opisującym hallotron jest
nazywana stałą hallotronu

Nawet wykonane z tego samego materiału hallotrony nie zawsze posiadają identyczne parametry, np. każdy posiada indywidualną charakterystykę. W związku z tym nawet w nieobecności pola magnetycznego między elektrodami, które trudno jest umieścić na jednej powierzchni ekwipotencjalnej, istnieje zazwyczaj napięcie
zwane napięciem niesymetrii, proporcjonalne do natężenia prądu zasilającego hallotron:

W układach pomiarowych napięcie asymetrii kompensuje się elektronicznie lub uprzednio wyznacza i następnie odejmuje od napięcia U.

Pomiar 1

Wyznaczanie zależności napięcia Halla od natężenia prądu zasilającego hallotron:

	I [mA]	UR [mV]	U [mV]	UH [mV]
1	1,888	-5,0	13,7	18,7
2	2,871	-7,6	20,9	28,0
3	3,860	-10,3	27,8	38,1
4	4,841	-12,9	34,7	47,6
5	6,806	-17,9	48,4	66,4
6	7,857	-20,4	55,2	75,2
7	8,831	-22,7	61,6	83,6
8	9,881	-25,0	68,2	93,2

Pomiary wykonaliśmy przy prądzie solenoidu I_S = (1500 ± 5) mA

Po wprowadzeniu danych do komputera równanie funkcji wygląda następująco:

y = 9,3243x + 1,7618

U_H = (9,3 ± 0,1)*

I = (1,8 ± 0,6)

Błędy:

• napięcia U : ± 0,2 mV

• napięcia asymetrii U_R : ± 0,2 mV

• napięcia Halla U_H :

Pomiar 2

Wyznaczanie zależności napięcia Halla od natężenia prądu zasilającego solenoid:

	IS [mA]	U [mV]	UH [mV]
1	560	7,1	33,87
2	670	13,1	39,87
3	780	19,9	46,67
4	890	26,7	53,47
5	970	31,9	58,67
6	1090	39,4	66,17
7	1180	44,9	71,67
8	1340	54,3	81,07
9	1480	63,5	90,27
10	1700	77,4	104,17

Pomiary wykonaliśmy dla :

• prądu zasilania I = ( 9,881 ± 0,002) mA

• napięcia asymetrii U_R = (-26,77 ± 0,2) mV

Dane zostały wprowadzone do komputera, który wyznaczył równanie prostej metodą regresji liniowej :

y = 0,0619x - 1,3824

U_H = (61,9 ± 0,4)*10 ^-3*

I_S = (-1,4 ± 0,3)

Błędy:

• napięcia U : ± 0,2 mV

• napięcia Halla U_H :

Pomiar 3

Wyznaczanie zależności napięcia Halla od położenia hallotronu na osi solenoidu:

	Z [cm]	U [mV]	UH [mV]
1	-9	22,5	49,07
2	-8	31,5	58,07
3	-7	39,9	66,47
4	-6	47,0	73,57
5	-5	52,7	79,27
6	-4	57,2	83,77
7	-3	60,3	86,87
8	-2	63,0	89,57
9	-1	64,0	90,57
10	0	64,9	91,47
11	1	64,7	91,27
12	2	63,9	90,47
13	3	62,5	89,07
14	4	60,4	86,97
15	5	57,4	83,97
16	6	53,2	79,77
17	7	47,9	74,47
18	8	40,6	67,17
19	9	32,8	59,37

Pomiary wykonaliśmy dla :

• prądu solenoidu I_S = (1500 ± 5) mA

• prądu zasilania I = (9,882 ± 0,001) mA

• napięcia asymetrii U_R = (-26,57 ± 0,2) mV

Błędy :

• napięcia U : ± 0,2 mV

• podziałki z : ± 0,1 cm

• napięcia Halla :
  

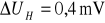
Wyznaczanie stałej hallotronu:

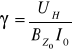
Jednak, abyśmy mogli obliczyć, musimy znać wartości indukcji pola magnetycznego B_Z, a wyraża się ona wzorem :

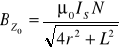
przyjmując : μ₀ , N, r, L = const

gdzie : k = 1,380⋅10^-2 T/A

Stąd indukcja pola magnetycznego dla prądu solenoidu I_S = 1500 mA wynosi :

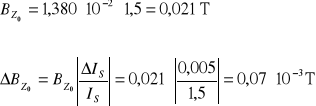
Prąd zasilania I₀ = 9,882 mA, zaś napięcie Halla U_H = 91,47 mV.

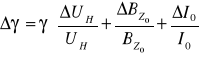
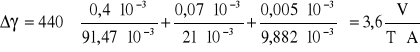
1

5

pole magnetyczne B

kierunek prądu I

P₁

P₂

---