Pomiar miąższości drzewa leżącego
PIEŃ I STRZAŁA
Pień - fragment nadziemnej części drzewa.
Oś morfologiczna - linia przechodząca wzdłuż pnia, przez środek rdzenia.
Strzała - pień, w którym możliwe jest prześledzenie osi morfologicznej od podstawy
do wierzchołka (świerk, sosna, jodła, modrzew). Z punktu widzenia pomiarów pień to część strzały.
Krzywa morfologiczna - linia ograniczająca przekrój podłużny strzały. Jej kształt jest nieregularny: u podstawy wklęsła, w części środkowej wypukła, w wierzchołkowej wklęsła, wypukła lub prosta. Zależy od gatunku, wieku, jakości siedliska, zwarcia itd.
Przekrój poprzeczny - fragment płaszczyzny prostopadłej do osi morfologicznej strzały ograniczony krzywą morfologiczną.
GEOMETRYCZNE BRYŁY OBROTOWE
Założenia:
OŚ MORFOLOGICZNA - prosta prostopadła do podstawy drzewa, przekroje poprzeczne są kołowe
Wtedy strzała - bryła powstała z obrotu figury ograniczonej krzywą morfologiczną, osią
![]()
morfologiczną i promieniem podstawy. Wzór tworzącej bryły:
y - promień bryły,
x - odległość promienia od wierzchołka,
p - parametr kształtu (stały dla danej bryły),
r - wykładnik kształtu (stały dla danej bryły).
Jest to wzór równania tworzącej regularnych brył obrotowych. Na kształt przekroju poprzecznego (przebieg tworzącej bryły) mają wpływ:
WYKŁADNIK KSZTAŁTU - stopień wklęsłości lub wypukłości tworzącej w stosunku do osi obrotu.
PARAMETR KSZTAŁTU - wielkość promienia bryły (im większy parametr kształtu, tym większy promień, w tej samej odległości od podstawy).
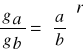
dany będzie przekrój poprzeczny ga, leżący w odległości a od wierzchołka, i przekrój gb, w odległości b to:jeżeli bryłę regularną podzieli się na części (sekcje) płaszczyznami prostopadłymi do osi obrotu, to każda z tych części będzie miała taki sam wykładnik kształtu, równy wykładnikowi kształtu bryły całkowitej.
PEŁNOŚĆ - miernikiem cechy jest wykładnik kształtu - gdy ten rośnie, pełność
(a z nią objętość) maleje.ZBIEŻYSTOŚĆ - miernikiem cechy jest różnica dwóch grubości z różnych miejsc bryły
(w cm.), podzielona przez odległość między tymi miejscami (w m.):SMUKŁOŚĆ - stosunek długości bryły (w m.) do grubość (w cm.), najczęściej mierzonej
na 1,3 m. od podstawy (dla strzały pierśnica):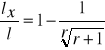
określ. wykł. ksz. na podst. położenia przekroju przeciętnego (sposób Grochowskiego).określanie wykładnika kształtu na podstawie długości części strzały o miąższości równej połowie miąższości całej strzały (sposób Bruchwalda).
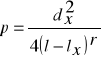
sposób Grochowskiego
dx - grubość odpowiadająca przekrojowi przeciętnemu.
r - wykładnik kształtu określony sposobem Grochowskiego.
sposób Bruchwalda
r - wykładnik kształtu określony sposobem Bruchwaldagrubość największa - dM
grubość najmniejsza - dm
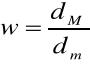
wydłużenie przekroju poprzecznego:kąt zawarty między największą i najmniejszą grubością przekroju kąt (mierzony w prawo) między kierunkiem północnym a największą grubością (kierunek wydłużenia przekroju poprzecznego).
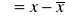
błąd absolutny - różnica wyniku pomiaru (x) i wielkości rzeczywistej (x):
błąd procentowy wtórny - błąd absolutny wyrażony w procentach wielkości rzeczywistej:
błąd procentowy zasadniczy - błąd absolutny wyrażony w procentach wyniku pomiaru: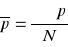
przy ocenie zbioru wyników pomiaru:
średnia arytmetyczna błędów procentowych:
odchylenie standardowe błędów procentowych:
uszeregowanie wzorów według malejącej dokładności:
- w. Hossfelda,
- w. środkowego przekroju,
- w. Smaliana.Dokładność wzorów zależy od wykładnika kształtu (decyduje o znaku i wielkości błędu)
i od stosunku średnicy górnej do dolnej (im większy tym większa dokładność).Poszczególne wzory są najmniej dokładne dla brył całkowitych (u = 0). Gdy u dąży
do 1 (walec) wtedy błąd poszczególnych wzorów dąży do 0.mały błąd poszczególnych sekcji (duże u), i mała miąższość ostatniej sekcji będącej bryłą całkowitą.
różna pełność poszczególnych sekcji - redukcja błędów o różnych znakach.
redukcja błędów pomiarów przy dużej ich liczbie.
dokładność rośnie gdy maleje długość sekcji (rośnie u) - dokładność wzorów sekcyjnych sprawdza się wzorami sekcyjnymi o krótszych sekcjach.
błąd teoretyczny ujemny - błąd empiryczny mniejszy ujemny, mniejszy
(wart. bezwzględna) dodatni lub większy dodatni (wart. bezwzględna).błąd teoretyczny dodatni - błąd empiryczny dodatni, większy.
błąd teoretyczny dodatni - błąd empiryczny mniejszy dodatni, mniejszy
(wart. bezwzględna) ujemny lub większy ujemny (wart. bezwzględna).błąd teoretyczny ujemny - błąd empiryczny ujemny, większy.
pierśnicowa liczba kształtu dla brył reg. zależy od wykładnika kształtu i wysokości.
taki sam wykładnik, różna wysokość - różna l. kształtu (mniejsza dla brył wyższych).
stała h (większa od 6,5 m), r rośnie w przedziale (0-3,5) - maleje l. kształtu.
stała h (w przedziale 2,1-6,5 m), r jak wyżej - l. k. najpierw maleje potem rośnie.
stała h (w przedziale 1,3-2,1 m), r jak wyżej - l. k. rośnie
pierśnicy - na ogół drzewa grubsze mają mniejszą p. l. k. W d-stanach średnich
i starszych klas wieku związek słaby lub nieistotny, silniejszy w młodnikach sosnowych
i d-stanach świerkowych i jodłowych.pierśnicy (słabiej niż od pierśnicy) - na ogół drzewa wyższe mają mniejszą p. l. k.
W d-stanach średnich i starszych klas wieku związek nieistotny, silniejszy w młodnikach sosnowych i d-stanach świerkowych i jodłowych.% grubości kory na pierśnicy - w d-stanach sosnowych związek średniej mocy, słabszy dla gatunków o cienkiej korze (buk, świerk, jodła): większy procent - mniejsza p. l. k.
ilorazu q2 () - większy iloraz - większa p. l. k. (silny związek).
miąższości drzewa i d-stanu, przyrostu miąższości drzewa i d-stanu.
pełności strzały (r można określić gdy oprócz f dane również h). Przydatność p. l. k.
do tego celu w d-stanach młodszych i starszych klas wieku mniejsza.właściwa liczba kształtu dla brył reg. zależy od wykładnika kształtu i n.
dla brył o takim samym r w. l. k. maleje ze wzrostem n.
stałe n (większe od 5,02) rośnie r - w. l. k. maleje.
stałe n (w przedziale 1,58-5,02), rośnie r (w przedziale 0-3,5) - w. l. k. ma minimum.
stałe n (w przedziale 1-1,52), rośnie r - w. l. k. rośnie.
dla określonej w. l. k. n jest stałe więc w. l. k. zależy tylko od r - jest miarą pełności.
pierśnicy (związek słabszy niż dla p. l. k.) - d-stany: korelacja dodatnia, starsze: ujemna.
wysokości (związek silniejszy niż dla p. l. k.) - korelacja dodatnia (drzewa wyższe - większa pełność). Zależność silniejsza w d-stanach młodych, słabsza w starych.
ilorazu qH () - silna korelacja dodatnia.
d-stany o małej pierśnicy i wysokości mają mniejszą w. l. k. niż te o wyższych wspomnianych parametrach. D-stany o wysokich przeciętnych wymiarach mają większą w. l. k. na siedliskach borowych.
l. k. to teoretycznie miernik pełności (korelacja dodatnia z r) jednak praktycznie nieprzydatna - duża rozbieżności tworzącej bryły równoważnej z krzywą morfologiczną przy podstawie. Z tych samych powodów nieprzydatna do określania miąższości drzewa stojącego.
Zaliczenie drzew d-stanu do czterech klas o równej liczebności, wyliczenie dla danej klasy: przeciętnej pierśnicy (na podstawie przeciętnego przekroju), oraz średniej wysokości (z równania krzywej wysokości, na podstawie przeciętnej pierśnicy)
Pobranie ośmiu drzew próbnych, po dwa dla każdej klasy. Wybierane są drzewa o pierśnicy i wys. zbliżonych do przeciętnej pierśnicy i średniej wysokości danej klasy. Na ich podstawie wyliczyć liczbę kształtu dla danej klasy.
Obliczenie i zsumowanie miąższości poszczególnych klas:
iloczyn przeciętnego przekroju ,liczebności, wysokości i liczby kształtu danej klasy.Przeliczenie otrzymanych wyników na 1 ha:
r |
równanie |
figura |
0 |
y = |
walec |
1 |
y2 = px |
paraboloida (wypukła) |
2 |
y = x |
stożek |
3 |
y2 = px3 |
neiloida (wklęsła) |
WŁASNOŚCI BRYŁ REGULARNYCH:
OBJĘTOŚĆ BRYŁ
![]()
Ogólny wzór na objętość całkowitej bryły obrotowej o równaniu tworzącej y2 = pxr:
go - przekrój podstawy bryły,
l - długość bryły.
Po zastosowaniu własności:
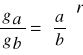
wzór przyjmuje postać:
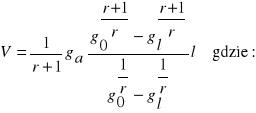
Ogólny wzór na objętość ściętej bryły obrotowej o równaniu tworzącej y2 = pxr:
go - przekrój dolny bryły.
gl - przekrój górny bryły.
KSZTAŁT PRZEKROJU PODŁUŻNEGO BRYŁ
Brył regularnych, strzał i ich części dotyczą następujące pojęcia:
![]()
d1 - średnica w miejscu odległym od wierzchołka bryły o x1,
d2 - średnica w miejscu odległym od wierzchołka bryły o x2.

Dla brył regularnych:
Jeżeli 0 < r < 2 to zbieżystość rośnie gdy maleje odległość sekcji od wierzchołka,
gdy r > 2 zbieżystość maleje gdy maleje odległość sekcji od wierzchołka.
Przy określaniu zbieżystości strzały liczy się ją dla dolnej części (np. wg. propozycji
![]()
Krenna):
Bryły mogą mieć taką samą pełność a różną zbieżystość i taką samą zbieżystość a różną pełność (cechy te są niezależne), najczęściej bryły bardziej pełne są mniej zbieżyste.

![]()
Dla brył regularnych:
Bryły o tej samej długości i tym samym parametrze kształtu będą miały tym większą smukłość, im większa będzie ich pełność.
SPOSOBY OKREŚLANIA WYKŁADNIKA KSZTAŁTU:
przekrój przeciętny - iloraz miąższości strzały i jej długości.
lx - odległość przekroju przeciętnego od podstawy strzały.
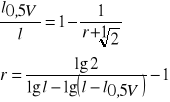
l0,5V - długość odziomkowej części strzały, której miąższość jest równa
połowie miąższości całej strzały.
SPOSOBY OKREŚLANIA PARAMETRU KSZTAŁTU:
Bryła równoważna strzale
BRYŁA RÓWNOWAŻNA STRZALE - bryła regularna o równaniu tworzącej y2 = pxr, dla której parametr i wykładnik kształtu określony został na podstawie cech strzały.
Parametr i wykładnik kształtu bryły równoważnej przyjmuje się jako cechy danej strzały.
Tworząca bryły równoważnej nie pokrywa się z krzywą morfologiczną strzały. Duże rozbieżności szczególnie w części dolnej i górnej brył (równanie y2 = pxr jest zbyt proste,
by odwzorować przebieg krzywej). Mniejsza rozbieżność między liniami występuje
w przypadku krótkich odcinków strzały.
Porównanie strzały i bryły równoważnej
sposób |
cechy wspólne strzały i bryły równoważnej |
Grochowskiego |
- długość |
Bruchwalda |
- długość |
KSZTAŁT PRZEKROJU POPRZECZNEGO BRYŁY
Kształt przekroju poprzecznego bryły jest kolisty, strzały - skomplikowaną figurą
Cechy opisujące kształt przekroju poprzecznego strzały:
OKREŚLANIE MIĄŻSZOŚCI STRZAŁ I CZĘŚCI STRZAŁ
Służą do tego wzory dendrometryczne zwykłe i sekcyjne.
Wzory zwykłe
![]()
Wyprowadza się je z zależności między polem przekroju bryły (g) i jego odległością
od podstawy (x):
Jeżeli długość bryły wynosi l, to:
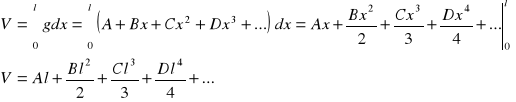
![]()
![]()
![]()
Z powyższego wzoru można opracować wiele wzorów dendrometrycznych:
![]()
![]()
dla brył ściętych:
Wzory sekcyjne
Podział bryły na odcinki (sekcje), określenie miąższości każdej sekcji wzorem zwykłym. Najczęściej stosowany wzór sekcyjny środkowego przekroju:
![]()
Wzór sekcyjny środkowego przekroju przy jednakowej absolutnej długości sekcji:
ls - długość sekcji.
Va - miąższość ostatniej, niepełnej sekcji określona wzorem zwykłym (bryły ścięte)
lub wzorem na objętość stożka (bryły całkowite).
Wzór sekcyjny środkowego przekroju przy jednakowej względnej długości sekcji
(liczbę sekcji zakłada się z góry):
![]()
n - liczba sekcji
Dokładność wzorów dendrometrycznych
Definicje błędów
Warunkiem wyznaczenia błędów jest dysponowanie wartością rzeczywistą
![]()
N - liczba spostrzeżeń w zbiorze.

TEORETYCZNA DOKŁADNOŚĆ WZORÓW DENDROMETRYCZNYCH
Ocenia się ją dla brył regularnych o równaniu tworzącej y2 = pxr.
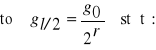
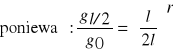
![]()
TEORETYCZNA DOKŁADNOŚĆ WZORU ŚRODKOWEGO PRZEKROJU:
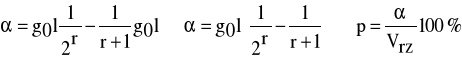
stąd:
Teoretyczna dokładność wzoru środkowego przekroju dla brył ściętych:
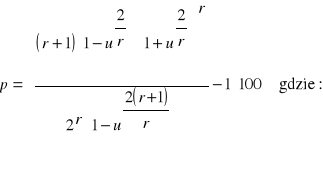


u - stosunek średnicy górnej do dolnej
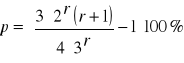
Teoretyczna dokładność wzoru Hossfelda
![]()
Teoretyczna dokładność wzoru Smaliana
PORÓWNANIE TEORETYCZNEJ DOKŁADNOŚCI WZORÓW DENDROMETRYCZNYCH
Teoretyczna dokładność wzorów dendrometrycznych dla brył całkowitych - błędy procentowe wtórne:
Wzór |
Wykładnik kształtu ( r ) |
||||||||
|
0 |
~0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
śr. przekroju |
0 |
0 |
6,06 |
0 |
-11,61 |
-25 |
-38,13 |
-50 |
-60,23 |
Hossfelda |
0 |
-25 |
-8,12 |
0 |
2,06 |
0 |
-4,74 |
-11,11 |
-18,35 |
Smaliana |
0 |
-50 |
-25 |
0 |
25 |
50 |
75 |
100 |
125 |
PARADOKS KSYLOMETRYCZNY
Bryła całkowita lub strzała może wykazać rachunkowo mniejszą objętość (miąższość) niż część tej bryły lub strzały. Dzieje się tak wtedy gdy wzór zastosowany do określenia objętości (miąższości) da błąd ujemny (większy dla bryły dłuższej, mniejszy dla krótszej
- redukowany przez u).
Wniosek - nie określać objętości (miąższości) górnej części bryły (strzały) z różnicy miąższości całości i części dolnej.
EMPIRYCZNA DOKŁADNOŚĆ WZORÓW DENDROMETRYCZNYCH
Ocenia się ją dla strzał lub ich części - porównanie miąższości wyliczonej wzorem dendrometrycznym z miąższością rzeczywistą (wzór sekcyjny).
Dokładność wzorów sekcyjnych
Przyczyny większej dokładności wzorów sekcyjnych od zwykłych:
EMPIRYCZNA DOKŁADNOŚĆ WZORÓW ZWYKŁYCH
Materiał - 94 letni drzewostan sosnowy (508 drzew, średnia wysokość 25,5 m., średnia pierśnica 30,8 cm.).
Empiryczna dokładność wzoru środkowego przekroju (bł. % wtórne, sekcja 1 m.):
rodzaj bryły |
zakres bł. |
średnia bł. |
bł. średni |
strzała w korze (65 % bł. -) |
-13,2 - 12,9 |
-1,76 |
4,07 |
strzała bez kory (88 % bł. +) |
-5,9 - 20,6 |
5,68 |
3,56 |
kłoda odziomkowa (0 - 8 m.) w korze |
-14,2 - -1,9 |
-7,20 |
2,39 |
kłoda odziomkowa (0 - 8 m.) bez kory (97 % bł. -) |
-9,4 - 6,6 |
-3,74 |
1,81 |
kłoda środkowa (0 - 8 m.) w korze |
-11,4 - 9,7 |
-0,13 |
1,84 |
kłoda środkowa (0 - 8 m.) bez kory |
-9,9 - 10,1 |
0,33 |
1,85 |
Empiryczna dokładność wzoru Hossfelda (bł. % wtórne):
rodzaj bryły |
zakres błędów |
średnia błędów |
błąd średni |
strzała w korze (86 % bł. -) |
-12,8 - 9,9 |
-3,43 |
3,40 |
strzała bez kory (77% bł. +) |
-7,9 - 13,6 |
2,08 |
2,92 |
kłoda odziomkowa (0 - 8 m.) w korze |
-14,4 - 5,2 |
-5,29 |
2,23 |
kłoda odziomkowa (0 - 8 m.) bez kory |
-8,5 - 4,6 |
-3,06 |
1,71 |
kłoda środkowa (0 - 8 m.) w korze |
-6,1 - 6,6 |
-0,46 |
1,53 |
kłoda środkowa (0 - 8 m.) bez kory |
-7,0 - 5,8 |
-0,31 |
1,48 |
|
|
|
|
Empiryczna dokładność wzoru Smaliana:
rodzaj bryły |
zakres błędów |
średnia błędów |
błąd średni |
strzała w korze |
34,5 - 180,0 |
86,85 |
16,65 |
strzała bez kory |
16,8 - 177,2 |
64,98 |
21,94 |
kłoda odziomkowa (0 - 8 m.) w korze |
10,8 - 103,7 |
42,41 |
10,94 |
kłoda odziomkowa (0 - 8 m.) bez kory |
7,9 - 95,5 |
39,48 |
11,40 |
kłoda środkowa (0 - 8 m.) w korze |
-11,3 - 9,2 |
-0,23 |
2,08 |
kłoda środkowa (0 - 8 m.) bez kory |
-11,9 - 6,3 |
-1,25 |
2,05 |
PRZYCZYNY NIEDOKŁADNOŚCI OKREŚLANIA MIĄŻSZOŚCI WZORAMI DENDROMETRYCZNYMI
NIEDOSTOSOWANIE WZORU DO KSZTAŁTU STRZAŁY W KIERUNKU PODŁUŻNYM:
Błąd zależy od wykł. kształtu (strzała), stosunku średnicy górnej do dolnej (część strzały) i rozbieżności między krzywą morf. strzały a tworzącą bryły obrotowej w miejscu pomiaru.
Tworząca bryły równoważnej wewnątrz krzywej morfologicznej:
Tworząca bryły na zewnątrz krzywej:
Tworząca bryły pokrywa się z krzywą - błąd teoretyczny = błąd empiryczny.
NIEDOSTOSOWANIE WZORU DO KSZTAŁTU STRZAŁY W KIERUNKU POPRZECZNYM:
Przekrój poprzeczny liczy się wzorem na pole koła lecz przekroje faktycznie odbiegają
od kołowych - zwłaszcza w dolnych partiach pnia (zgrubienia korzeniowe) - por. dokładność wzoru Smaliana.
Błędy przy pomiarze elementów miąższości:
Błędy przy pomiarze długości i grubości - niedokładność przyrządów i wykonywania pomiarów (szczególnie starannie należy mierzyć grubość - jej błędy znacząco wpływają
na błąd miąższości). Przy wielu pomiarach i zaokrągleniach błędy wynikłe z niedokładności
mogą się redukować.
OKREŚLANIE LICZBY KSZTAŁTU I WYSOKOŚCI KSZTAŁTU
Pierśnicowa liczba kształtu
Pierśnicowa liczba kształtu - stosunek miąższości drzewa do objętości walca o wysokości równej wysokości drzewa i polu podstawy równym pierśnicowemu polu przekroju drzewa:
![]()
Rodzaje liczb kształtu:
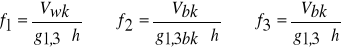
Pierśnicowe liczby kształtu strzały:
Pierśnicowa liczba kształtu grubizny drzewa:
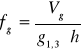
Gdzie:
![]()
Vg - miąższość grubizny strzały w korze wraz m miąższością grubizny gałęzi
Pierśnicowa liczba kształtu całego drzewa:
![]()
![]()
licznik - miąższość całego drzewa w korze.
TEORETYCZNA ANALIZA PIERŚNICOWEJ LICZBY KSZTAŁTU:
![]()
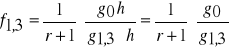
Objętość regularnych brył obrotowych o równaniu tworzącej y2 = pxr:
Dzielenie objętości bryły przez objętość walca porównawczego daje pierśnicową l. kształtu:
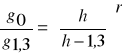
Ponieważ:
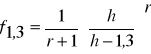
wzór przyjmuje postać:
Analiza wzoru na podstawie badań Głąbińskiego:
Zmienność pierśnicowej liczby kształtu i jej zależność od niektórych cech drzewa
Zmienność p. l. k. dość duża (współczynnik zmienności dla d-stanów sosnowych 6-9 %).
Pierśnicowa liczba kształtu zależy od:
ZASTOSOWANIE PIERŚNICOWEJ LICZBY KSZTAŁTU
Podstawa opracowania systemu pomiaru lasu w praktyce i doświadczalnictwie:
WŁAŚCIWA LICZBA KSZTAŁTU
Teoretyczna analiza właściwej liczby kształtu
![]()
WŁAŚCIWA LICZBA KSZTAŁTU - stosunek miąższości drzewa do objętości walca, którego wysokość jest równa wysokości drzewa a pole podstawy polu przekroju drzewa na wysokości h/n:
n - dowolna liczba większa od jedności (najczęściej 10).
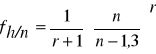
Dla regularnych brył obrotowych o równaniu tworzącej y2 = pxr wzór na w. l. k. ma postać:
Analiza wzoru:
Zmienność właściwej liczby kształtu (n = 10) i jej zależność od niektórych cech drzewa
Współczynnik zmienności dla d-stanów sosnowych :4-7 % - mniejszy niż dla p. l. k.
Właściwa liczba kształtu zależy od:
ZASTOSOWANIE WŁAŚCIWEJ LICZBY KSZTAŁTU
Metody oceny miąższości oparte na w. l. k. nie znalazły praktycznego zastosowania (przekrój h/n leży na różnych wysokościach). Liczba ta ma znaczenie jako miernik pełności.
ABSOLUTNA LICZBA KSZTAŁTU
![]()
ABSOLUTNA LICZBA KSZTAŁTU - stosunek miąższości drzewa do objętości walca o wysokości równej wysokości drzewa i o przekroju równym przekrojowi podstawy drzewa:
A. l. k. stanowi granicę, do której dąży w. l. k., gdy n dąży do nieskończoności.
![]()
Dla regularnych brył obrotowych o równaniu tworzącej y2 = pxr wzór na a. l. k. ma postać:
WYSOKOŚĆ KSZTAŁTU
![]()
Wysokość kształtu - iloczyn wysokości drzewa i pierśnicowej liczby kształtu (wysokość walca o średnicy równej pierśnicy drzewa i objętości takiej jak miąższość drzewa):
W. k. służy do określania miąższości drzewa i d-stanu (tablice wysokości kształtu).
Określanie miąższości drzewa stojącego
Wzory dendrometryczne nieprzydatne - trudno przeprowadzić pomiar.
OKREŚLANIE MIĄŻSZOŚCI DRZEWA STOJĄCEGO TABLICAMI LICZB KSZTAŁTU I WYSOKOŚCI KSZTAŁTU
![]()
Miąższość drzewa można określić wzorem:
Występującą we wzorze f1,3 odczytuje się z tablic liczb kształtu; dla gatunku i wysokości (proste ale mało dokładne tablice Krzysika i Ochrymowicza) lub gatunku pierśnicy
i wysokości (t. Grundnera-Schwappacha czy t. Radwańskiego dla sosny do 80 lat i starszych). W najdokładniejszych tablicach brany jest pod uwagę iloraz q2 lecz nie mają one praktycznego zastosowania - trudności w pomiarach (t. Schiffla). Dokładność tablic zależy od liczby cech wziętych pod uwagę oraz stopnia ich powiązania z pierśnicową liczbą kształtu, doboru ilości i jakości materiału empirycznego wziętego
do budowy tablic, jak również sposób ich budowy.
OKREŚLANIE MIĄŻSZOŚCI DRZEWA STOJĄCEGO TABLICAMI MIĄŻSZOŚCI
Dla poszcz. gat. na podstawie pierśnicy i wysokości (sosna dodatkowo do 80 lat i dla starszej)
Tabl. Grundnera, Schwappacha, t. Czuraja, Radwańskiego, Strzemeskiego, t. Radwańskiego.
BŁĄD TABLIC - wynika z rozbieżności między liczbami kształtu użytymi do obliczenia miąższości tablicowych z rzeczywistymi l. ksz. badanych drzew. O dokładności decydują te same czynniki co przy tablicach liczb kształtu (patrz 8 linijek wyżej). Dokł. nie jest duża (nawet pow. 100 % dla młodych drzew - lepsza dla d-stanów; błędy dla drzew redukują się).
Jeżeli wynik ma być dokładny może zachodzić konieczność wykonania podwójnej interpolacji - ze względu na pierśnicę i wysokość:
Przykład dla d = 38,5 cm i h = 23,5 m.
V38,23 = 1,13 V38,24 = 1,18 V38,23,5 = 1,155
V39,23 = 1,19 V39,24 = 1,24 V39,23,5 = 1,215
V38,23,5 = 1,155 V39,23,5 = 1,215 V38,5,23,5 = 1,185
Określanie miąższości wzorem Denzina
V=0,001d2
Zaletą wzoru - prostota, wadą mała dokł. (niezłe wyniki jedynie dla sosny o h około 30 m)
Określanie miąższości strzały i części strzały bez kory
Tablice Radwańskiego - podają grubość bez kory w różnych miejscach strzały oraz miąższość bez kory od podstawy do różnych wysokości - umożliwia to określenie miąższości bez kory części pnia z dowolnej wysokości na podst. pierśnicy w korze i wysokości drzewa
MIĄŻSZOŚĆ DRZEWOSTANU
V = GHF gdzie:
G - pierśnicowe pole przekroju drzewostanu,
H - średnia wysokość drzewostanu,
F - pierśnicowa liczba kształtu drzewostanu.
Określanie elementów miąższości
Średnia arytmetyczna pierśnic drzew drzewostanu

Pierśnicowe pole przekroju drzewostanu
G = n1g1 + n2g2 + ... + nugu
gdzie:
n1 ,n2,... nu - liczba drzew w poszczególnych stopniach grubości.
g1, g2, ... gu - przekroje odpowiadające wartościom środkowym stopni pierśnic.
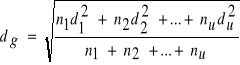
Przeciętna pierśnica przekrojowa
Jest to średnia kwadratowa - przyjmuje większe wartości od średniej arytmetycznej pierśnic.
Odchylenie standardowe i współczynnik zmienności pierśnic drzew drzewostanu.
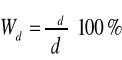
Odchylenie standardowe (σd) 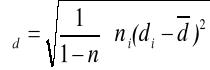

to pierwiastek kwadratowy z wariancji, którą dla szeregu rozdzielczego liczy się według wzoru: współ. zmienności
Współczynnik zmienności pierśnicowego pola przekroju d-stanu
Wg =2Wd
Liczba drzew potrzebna do określenia danej cechy drzewostanu, z określonym błędem, przy poziomie istotności 0,32 (poziom ufności 0,68).
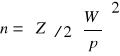
Liczebność próby (n), przy znanym współczynniku zmienności (W) i dopuszczalnym błędzie (p) wyznacza się ze wzoru:
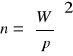
Przy poziomie ufności 0,68 Z/2 = 1 - wzór przyjmuje postać:
Wysokość
Krzywa wysokości - pomiar pierśnicy i wysokości pewnej liczby drzew d-stanu, wybranych z całego zakresu pierśnic, sporządzenie wykresu: oś odciętych - pierśnica, oś rzędnych - wysokość. Przez układ punktów na wykresie przeprowadza się linię wyrównującą (najczęściej odręcznie lub matematycznie - metodą najmniejszych kwadratów z zastosowaniem wzoru Näslunda albo hiperboli). Z otrzymanej krzywej wysokości można określić wysokość dowolnego stopnia pierśnicy.
Określanie średniej wysokości d-stanu
Wzór Lorey'a:
hL =
Wzór częściej stosowany w dendrometrii (jest to średnia ważona pierśnicowym polem przekroju d-stanu, która to cecha jest dodatnio skorelowana z wysokością d-stanu, daje on dlatego większe wartości niż zwykła średnia arytmetyczna, zbliżone do tych, które można odczytać z krzywej wysokości dla przeciętnej pierśnicy).
Współczynnik zmienności wysokości i współczynnik zmienności wysokości, z wyłączonym wpływem pierśnicy można wyznaczyć za pomocą empirycznych równań:
WH = 4,55 + 135,95
WH.D = 4,48 + 42,75
![]()
Błąd określania przeciętnej wysokości d-stanu (błąd krzywej wysokości), przy poziomie istotności 0,32 (poziom ufności 0,68).
Pierśnicowa liczba kształtu
Pierśnicowa liczba kształtu d-stanu:
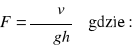
Określa się na podstawie wyników pomiaru drzew próbnych wg. wzoru:
Pierśnicowa liczba kształtu stopni pierśnic
Sporządza się linię liczb kształtu na podstawie drzew próbnych wybranych z całego zakresu pierśnic (wykres przedstawiający zależność liczby kształtu od pierśnicy - oś rzędnych - pierśnica, oś odciętych - pierśnicowa liczba kształtu drzewa próbnego). Z linii liczb kształtu można odczytać pierśnicową liczbę kształtu dla każdego stopnia pierśnicy.
Dokładność określania pierśnicowej liczby kształtu
Przy pobieraniu drzew próbnych można kierować się cechami od których zależy pierśnicowa liczba kształtu. Zwiększa to dokładność jej określania co charakteryzują poniższe zależności:
![]()
Współczynniki zmienności liczby kształtu drzewostanu z wyłączonym wpływem:
![]()
pierśnic: wysokości ![]()
ilorazu q2
![]()
procentu grubości kory na pierśnicy ![]()
pierśnicy i wysokości
![]()
pierśnicy i proc. grub. kory na pier. ![]()
pierśnicy,wys. i proc.grub.kory na p.
r - współczynnik korelacji między odpowiednimi cechami
Błędy średnie liczby kształtu d-stanu określonej na podstawie drzew próbnych wybieranych jako przeciętne pod względem następującej cechy pomocniczej:

pierśnicy (nd = N) 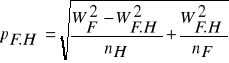
wysokości
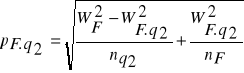
ilorazu q2. 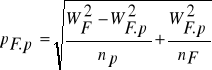
procentu grubości kory na pierśnicy.
Pierśnicową liczbę kształtu stopnia grubości można także odczytać z tablic liczb kształtu dla drzew. P. l. k. d-stanu można wyznaczyć z wzorów empirycznych.
Określanie miąższości d-stanu
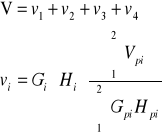
METODA URICHA, PRZY 8 DRZEWACH PRÓBNYCH.
Tok postępowania:
Metodą linii liczb kształtu
Sporządzić linię liczb kształtu. Odczytać z niej liczby kształtu poszczególnych stopni grubości. Obliczyć miąższość stopnia grubości wg. wzoru:
Zsumować miąższość poszczególnych stopni grubości, wynik przeliczyć na hektar. ![]()
Dokładność metod.
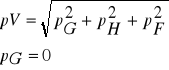
Błąd miąższości:
BŁĄD MIĄŻSZOŚCI W METODZIE URICHA.
W tej metodzie dla poszczególnych klas wybiera się drzewa próbne o wysokości i pierśnicy zbliżonej do średniej wysokości i przeciętnej pierśnicy danej klasy, tak więc do obliczenia błędu miąższości należy wziąć błąd liczby kształtu określonej na podstawie nF (tu 8) drzew próbnych, wybranych jako przeciętne pod względem pierśnicy (określonej na podstawie całej populacji - nd = N) i wysokości (wyznaczonej na podstawie nH drzew próbnych - tyle ile
uwzględniło się przy sporządzaniu krzywej wysokości):
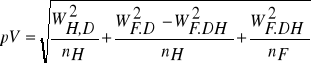
BŁĄD MIĄŻSZOŚCI W METODZIE LINII LICZB KSZTAŁTU.
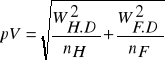
W metodzie tej liczby kształtu odpowiadające poszczególnym stopniom pierśnic wyznacza się z równania krzywej charakteryzującej zależność pierśnicy i liczby kształtu, więc do obliczenia błędu miąższości należy wziąć błąd liczby kształtu z wyłączonym wpływem pierśnicy:
MIĄŻSZOŚĆ GRUBIZNY DRZEWOSTANU:
Miąższość grubizny drzewostanu wzorem empirycznym.
Wzór ma postać:
v - średnia miąższość drzew stopnia pierśnicy,
H - średnia wysokość drzew stopnia pierśnicy,
D - średnia pierśnica drzewostanu,
d - wartość środkowa stopnia pierśnicy.
Po wyliczeniu miąższości grubizny dla stopni grubości należy je zsumować a wynik przeliczyć na hektar. Miąższość grubizny stopnia grubości można odczytać z tablic IBL.
PRZYROST MIĄŻSZOŚCI DRZEWOSTANU
![]()
Przyrostu miąższości drzewa leżącego sposobem sekcyjnym
V - miąższość drzewa w końcu okresu,
v - miąższość drzewa w początku okresu.
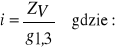
Intensywność przyrostu miąższości
g1,3 - pole przekroju pierśnicowego w końcu okresu w korze.
Linia przyrostu pierśnic - pomiar pierśnic i przyrostów pierśnic pewnej ilości drzew. Wykres: oś rzędnych - przyrost pierśnicy, oś odciętych - pierśnica. Przez punkty na wykresie przeprowadza się linię wyrównującą. Z otrzymanej linii przyrostu pierśnic można określić średnią wartość przyrostu pierśnicy dla każdego stopnia grubości.
Obliczanie przyrostu miąższości drzewostanu za pomocą drzew próbnych metodą M. BOROWSKIEGO

Na podstawie analizy krzywej frekwencji stopni pierśnic (wieloboku liczebności) dobiera się liczbę drzew próbnych reprezentujących poszczególne stopnie (ich liczba zależy od liczebności stopnia). Należy wybrać drzewa o przyroście pierśnicy (linia przyrostu pierśnic)
i wysokości zbliżonych do średnich wartości tych cech dla danego stopnia. Na podstawie drzew próbnych wyznacza się intensywność przyrostu miąższości drzewostanu (i) a następnie przyrost miąższości drzewostanu (Zv):
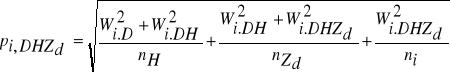
Dokładności metody M. Borowskiego.
Przyrost miąższości d-stanu określony za pomocą tablic przyrostu miąższości M. Borowskiego
Na podstawie przyrostu pierśnicy (linia przyrostu pierśnic), pierśnicy i wysokości stopnia grubości odczytuje się przyrost miąższości, który po pomnożeniu przez jego liczebność daje przyrost miąższości stopnia grubości. Suma przyrostów w stopniach grubości daje przyrost miąższości d-stanu.
Przyrost miąższości d-stanu za pomocą drzew próbnych metodą właściwej liczby kształtu f1/3 (metoda Bruchwalda).
![]()
Linia grubości kory - na pewnej liczbie drzew zmierzyć pierśnicę podwójną grubość kory na pierśnicy. Dane nanieść na wykres: oś rzędnych - podwójna grubość kory, oś odciętych - pierśnica. Przeprowadzić linię wyrównującą. Z wykresu można odczytać podwójną grubość kory dla dowolnego stopnia grubości.
Określanie przyrostu miąższości:
V - miąższość dla końca okresu,
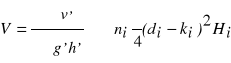
v - miąższość dla początku okresu.
Pierwsza część wzoru to pierśnicowa liczba kształtu strzały bez kory (f2) drzewostanu, wyznaczona na podstawie cech dowolnie wybranych drzew próbnych, druga to suma iloczynów liczebności stopnia, jego pierśnicowego pola przekroju bez kory i średniej wysokości stopnia.
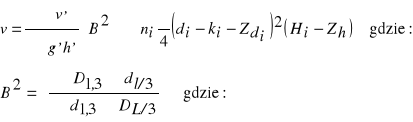
Suma iloczynów objętości walców porównawczych stopni pierśnic i liczebności tych stopni, na końcu okresu:
Zh - średni przyrost wysokości wyznaczony na podstawie drzew próbnych (podobnie jak sumy wyrażenia B2).
D1,3 - pierśnica bez kory w końcu okresu,
D1,3 - pierśnica bez kory na początku okresu,
Dl/3 - grubość bez kory na 1/3 długości strzały w końcu okresu,
Dl/3 - grubość bez kory na 1/3 długości strzały na początku okresu.
Strona 20 z 22
Strona 21 z 22
![]()
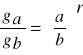
![]()
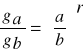

![]()
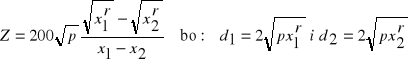
![]()

![]()
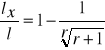
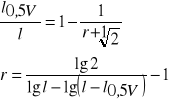
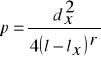
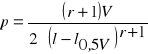
![]()
![]()
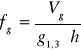
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
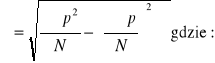

![]()

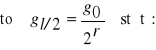

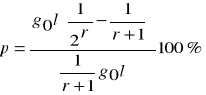
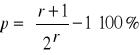
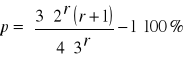
![]()
![]()
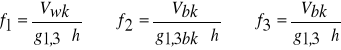
![]()
![]()
![]()
![]()
![]()

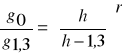

![]()
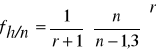
![]()
![]()
![]()
![]()

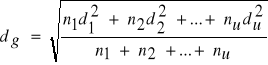
![]()
![]()
![]()

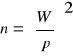
![]()
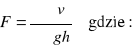
v-miąższość drzew próbnych, g- pierśnicowe pole przekroju d. próbnych, h-wysokość d. próbnych.
g
![]()
![]()
![]()
![]()
![]()
![]()
![]()
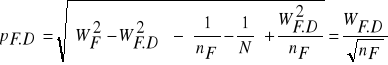
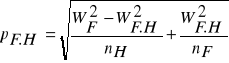
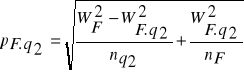

G - pierśnicowe pole przekroju klasy,
H - średnia wysokość klasy,
Vp - miąższość drzewa próbnego,
Gp - pierśnicowe pole przekroju drzewa
próbnego,
Hp - wysokość drzewa próbnego.

![]()

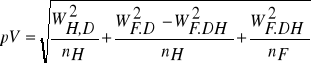
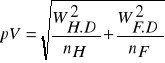
v
d
40000
h
f
c
h
H
(72,233
3,7D
6,275H)
1
D
1
d
f
0,404997
1,161508
H
1,3
0,030659
H
1,360943
H
D
d
c
1,004
106,25
d
2
2
3
2
(
![]()
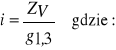
zv -przyrost miąższości drzewa próbnego, g1,3 - pierśnicowe pole przekroju drzewa próbnego, G1,3 - pierśnicowe pole przekroju drzewostanu.
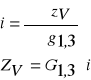

![]()
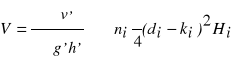

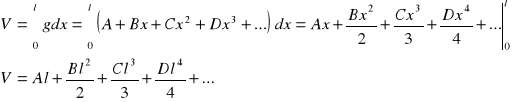
Wyszukiwarka
Podobne podstrony:
Pomiar wysokości drzewa
drzewa - wyklady, Studia, I rok, I rok, II semestr, Dendrologia
2013 AK sem3 I kolokwium-pyt przyk, STUDIA, SGGW, dendrologia, drzewa iglaste
Kolokwium dendrologia 2.podziałka (2), STUDIA, SGGW, dendrologia, drzewa liściaste
AK Drzewoznawstwo sem 3, STUDIA, SGGW, dendrologia, drzewa iglaste
2014 Pomiar wysokości przy przyjęciu za wierzchołek drzewa wierzchołka
download Zarządzanie Produkcja Archiwum w 09 pomiar pracy [ www potrzebujegotowki pl ]
2 1 Podstawowe czynności pomiarowe w geodezji
BYT 2005 Pomiar funkcjonalnosci oprogramowania
6 PKB 2 Pomiar aktywności gospodarczej rozwin wersja
Praktyczna interpretacja pomiarów cisnienia
wyklad 13nowy Wyznaczanie wielkości fizykochemicznych z pomiarów SEM
13a Pomiary jakosci
NIEPEWNOŚĆ POMIARU
Strategia pomiarów środowiska pracy
PEM (10) Nieoewność pomiaru
2 8 Błedy pomiarów
więcej podobnych podstron