Ćwiczenie II-3
Temat: Pomiar widma absorbcyjnego półprzewodnika w okolicy krawędzi absorbcji. Wyznaczanie szerokości przerwy energetycznej.
1. Cel ćwiczenia
- Teoretyczne zapoznanie się z podstawowymi mechanizmami absorbcji w półprzewodnikach
- Zapoznanie się z przyrządami optycznymi potrzebnymi do pomiaru widma absorbcyjnego (źródło światła + monochromator + detektor = spektrometr).
- Pomiar i wykreślenie widma w okolicy krawędzi absorbcji półprzewodnika oraz wyznaczenie szerokości prxerwy energetycznej.
2. Podstawy teoretyczne.
Zgodnie z modelem pasmowym półprzewodników elektrony i dziury mogą przyjmować tylko określone stany energetyczne zwane pasmami. Najniższe z nich zwane jest walencyjnym i odgrodzone jest od wyższych (pasm przewodnictwa) strefą wzbronioną. Wielkość tej strefy zależy od rodzaju półprzewodnika i decyduje o jego własnościach jak przewodnictwo elektryczne, przewodnictwo cieplne i fotoprzewodnictwo. Jedną z metod wyznaczania przerwy wzbronionej Eg jest metoda oparta na pomiarze współczynnika absorbcji w funkcji energii promieniowania elektromagnetycznego padającego na próbkę półprzewodnika. Ponieważ istnieje kilka rodzajów absorbcji (podstawowaprosta i skośna, dozwolona i zabroniona; ekscytonowa, domieszkowa, sieciowa i przez swobodne ładunki) i wszystkie one wpływają na wynik pomiaru, należy na podstawie znajomości struktury półprzewodnika założyć dominujący rodzaj pochłaniania i wedłufg tych założeń dokonywać obliczeń. Dla poniższych doświadczeń przejściem dominującym jest przejście proste dozwolone, dla którego widmo absorbcyjne przybliżyć możemy następującą funkcją:
α=B*(hν-ΔEg)1/2
Absorbcję światła opisuje prawo Lamberta:
J=J0 (1-R)e-αd
gdzie : J0 - natężenie światła padającego na badaną substancję
J - natężenie po przejściu przez substancję
α - współczynnik absorbcji
d - grubość warstwy
R - współczynnik odbicia.
Transmisja próbki jest to stosunek natężenia fali po przejściu do natężenia fali padającej:
T=J/J0
W tym doświadczeniu za wartość proporcjonalną do transmisji uznano stosunek napięć na fotodiodzie - napięcia z próbką do napięcia bez próbki:
T0=U/U0
Po uwzględnieniu odbicia od powierzchni badanej substancji :
T=T0 / (1-R)
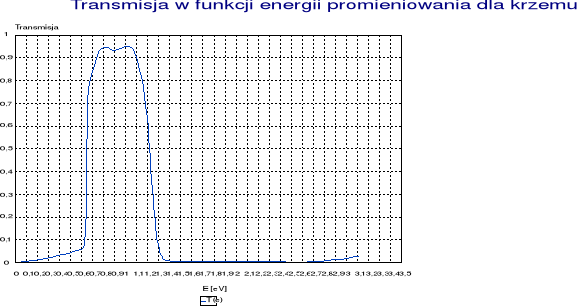
Gdy energia padającego promieniowania zbliży się do krawędzi absorbcji transmisja próbki gwałtownie rośnie. Widać to na wykresach 1,2,3 i 4 (uwaga - należy je oglądać od prawej do lewej, tak jak rośnie fługość fali).
Szerokość przerwy wzbronionej ΔEg wyznaczyć możemy badając przebieg transmisji w funkcji energii (patrz wykresy, też od prawej do lewej) lub dokładniej przez rozwiązanie następującego równania:
[log (T)]2=E(hν)
Numeryczne rozwiązanie tego równanie dla badanych substancji przedstawiają ostatnie kolumny tabelek, wersy wyróżnione są przybliżonym rozwiązaniem.
Wartość R przyjęto jako 15 - 45 %.
3. Pomiar przerw wzbronionej dla krzemu, arsenku galu, fosforku indu i nieznanej próbki.
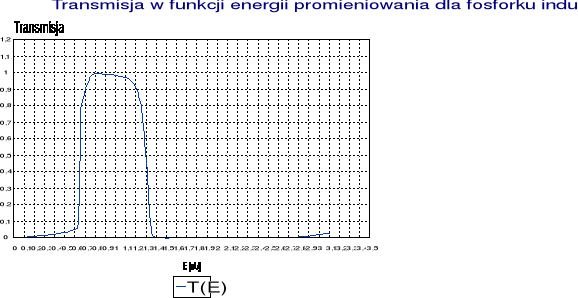
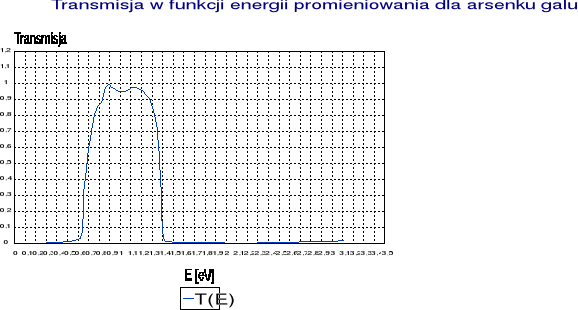
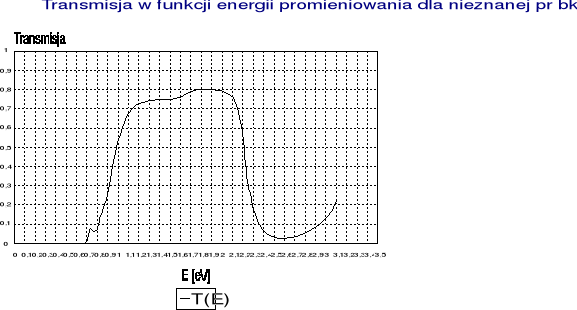
Dla każdej próbki dokonano pomiarów przy użyciu przetwornika germanowego i miliwoltomierza. Błąd pomiaru *1 cyfra i błąd rozdzielczości monochromatora pominięto. Wyniki pomiarów przedstawiają : - dla Si - tabela 1, dla GaAs - tabela 2, dla InP - tabela 3 i dla nieznanej próbki tabela 4 oraz wykresy o analogicznych numerach.
Otrzymano następujace wyniki
ΔEg(Si)=1,294*0,013 [eV]
ΔEg(GaAs)= 1,380*0,008 [eV]
ΔEg(InP)= 1,321*0,012 [eV]
ΔEg(???)=1,015*0,02 [eV]
Schemat aparatury użytej do pomiarów przedstawia rysunek załączony na ostatniej stronie.
λ[μm] |
E[eV] |
T |
(log(t))^2 |
log-E |
0.40 |
3.105 |
0.0278 |
2.4221 |
-0.6829 |
0.45 |
2.760 |
0.0056 |
5.0863 |
2.3263 |
0.50 |
2.484 |
0.0023 |
6.9458 |
4.4618 |
0.55 |
2.258 |
0.0055 |
5.1045 |
2.8464 |
0.60 |
2.070 |
0.0048 |
5.3637 |
3.2937 |
0.65 |
1.911 |
0.0046 |
5.4737 |
3.5629 |
0.70 |
1.774 |
0.0049 |
5.3313 |
3.5570 |
0.75 |
1.656 |
0.0052 |
5.2057 |
3.5497 |
0.80 |
1.553 |
0.0062 |
4.8690 |
3.3165 |
0.85 |
1.461 |
0.0062 |
4.8745 |
3.4133 |
0.90 |
1.380 |
0.0091 |
4.1752 |
2.7952 |
0.92 |
1.350 |
0.0129 |
3.5707 |
2.2207 |
0.94 |
1.321 |
0.0319 |
2.2400 |
0.9187 |
0.96 |
1.294 |
0.0786 |
1.2198 |
-0.0739 |
0.98 |
1.267 |
0.1759 |
0.5697 |
-0.6977 |
1.00 |
1.242 |
0.3186 |
0.2467 |
-0.9953 |
1.05 |
1.183 |
0.6860 |
0.0268 |
-1.1561 |
1.10 |
1.129 |
0.8443 |
0.0054 |
-1.1237 |
1.15 |
1.080 |
0.9222 |
0.0012 |
-1.0788 |
1.20 |
1.035 |
0.9511 |
0.0005 |
-1.0345 |
1.30 |
0.955 |
0.9416 |
0.0007 |
-0.9547 |
1.40 |
0.887 |
0.9346 |
0.0009 |
-0.8863 |
1.50 |
0.828 |
0.9469 |
0.0006 |
-0.8274 |
1.60 |
0.776 |
0.9362 |
0.0008 |
-0.7754 |
tabela 1 - Si
λ[μm] |
E[eV] |
T |
(log(t))^2 |
log-E |
0.40 |
3.105 |
0.0152 |
3.3011 |
-3.2859 |
0.45 |
2.760 |
0.0091 |
4.1565 |
-4.1474 |
0.50 |
2.484 |
0.0051 |
5.2626 |
-5.2575 |
0.55 |
2.258 |
0.0008 |
9.7468 |
-9.7460 |
0.60 |
2.070 |
0.0011 |
8.8477 |
-8.8467 |
0.65 |
1.911 |
0.0014 |
8.0840 |
-8.0825 |
0.70 |
1.774 |
0.0020 |
7.3018 |
-7.2998 |
0.75 |
1.656 |
0.0029 |
6.4628 |
-6.4599 |
0.80 |
1.553 |
0.0056 |
5.0774 |
-5.0718 |
0.85 |
1.461 |
0.0086 |
4.2763 |
-4.2678 |
0.87 |
1.428 |
0.0094 |
4.1166 |
-4.1073 |
0.89 |
1.396 |
0.1237 |
0.8238 |
-0.7002 |
0.90 |
1.380 |
0.3821 |
0.1746 |
0.2074 |
0.95 |
1.307 |
0.8486 |
0.0051 |
0.8436 |
1.00 |
1.242 |
0.9292 |
0.0010 |
0.9281 |
1.10 |
1.129 |
0.9735 |
0.0001 |
0.9733 |
1.20 |
1.035 |
0.9462 |
0.0006 |
0.9456 |
1.30 |
0.955 |
0.9611 |
0.0003 |
0.9608 |
1.40 |
0.887 |
0.9916 |
0.0000 |
0.9916 |
1.50 |
0.828 |
0.8908 |
0.0025 |
0.8883 |
1.60 |
0.776 |
0.8356 |
0.0061 |
0.8295 |
tabela 2 - GaAs
λ[μm] |
E[eV] |
T |
(log(t))^2 |
log-E |
0.4 |
3.105 |
0.0284 |
2.3918 |
2.3634 |
0.45 |
2.760 |
0.0057 |
5.0423 |
5.0366 |
0.5 |
2.484 |
0.0036 |
6.0007 |
5.9971 |
0.55 |
2.258 |
0.0014 |
8.1318 |
8.1304 |
0.6 |
2.070 |
0.0015 |
8.0037 |
8.0023 |
0.65 |
1.911 |
0.0007 |
10.0802 |
10.0795 |
0.7 |
1.774 |
0.0008 |
9.6151 |
9.6144 |
0.75 |
1.656 |
0.0007 |
10.0802 |
10.0795 |
0.8 |
1.553 |
0.0006 |
10.4860 |
10.4854 |
0.85 |
1.461 |
0.0006 |
10.2113 |
10.2107 |
0.9 |
1.380 |
0.0063 |
4.8534 |
4.8471 |
0.92 |
1.350 |
0.0588 |
1.5140 |
1.4552 |
0.94 |
1.321 |
0.2890 |
0.2906 |
0.0016 |
0.96 |
1.294 |
0.5216 |
0.0799 |
-0.4417 |
0.98 |
1.267 |
0.7159 |
0.0211 |
-0.6948 |
1 |
1.242 |
0.8214 |
0.0073 |
-0.8141 |
1.1 |
1.129 |
0.9644 |
0.0002 |
-0.9642 |
1.2 |
1.035 |
0.9796 |
0.0001 |
-0.9795 |
1.3 |
0.955 |
0.9919 |
0.0000 |
-0.9919 |
1.4 |
0.887 |
0.9887 |
0.0000 |
-0.9887 |
1.5 |
0.828 |
0.9980 |
0.0000 |
-0.9980 |
1.6 |
0.776 |
0.9891 |
0.0000 |
-0.9890 |
tabela 3 - InP
λ[μm] |
E[eV] |
T |
(log(t))^2 |
log-E |
0.4 |
3.105 |
0.2273 |
1.6561 |
1.4289 |
0.45 |
2.760 |
0.0455 |
7.2084 |
7.1629 |
0.5 |
2.484 |
0.0341 |
8.6126 |
8.5785 |
0.55 |
2.258 |
0.2815 |
1.2126 |
0.9312 |
0.6 |
2.070 |
0.7747 |
0.0492 |
-0.7255 |
0.7 |
1.774 |
0.7992 |
0.0379 |
-0.7612 |
0.8 |
1.553 |
0.7550 |
0.0596 |
-0.6954 |
0.9 |
1.380 |
0.7473 |
0.0640 |
-0.6833 |
1 |
1.242 |
0.7342 |
0.0720 |
-0.6622 |
1.1 |
1.129 |
0.6967 |
0.0985 |
-0.5982 |
1.2 |
1.035 |
0.5862 |
0.2152 |
-0.3710 |
1.3 |
0.955 |
0.4253 |
0.5516 |
0.1263 |
1.4 |
0.887 |
0.2294 |
1.6354 |
1.4060 |
1.5 |
0.828 |
0.1423 |
2.8684 |
2.7261 |
1.6 |
0.776 |
0.0623 |
5.8137 |
5.7514 |
tabela 4 - ??
4. Pomiar charakterystyk fotoogniwa krzemowego (fotodiody) i fotoogniwa germanowego względem charakterystyki termopary.
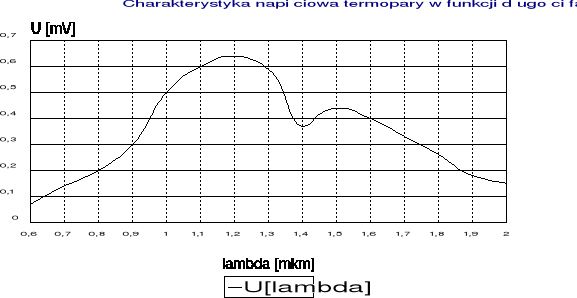
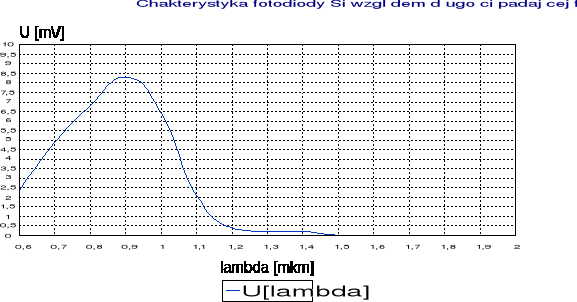
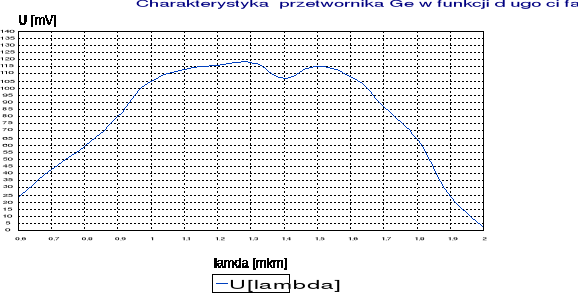
W tym doświadczeniu zbadano charakterystyki przetworników: termopary, fotodiody krzemowej i germanowej. Wyniki pomiarów pokazuje tabelka oraz wykresy.
Na podstawie obserwacji stwierdzić można że:
1. Termopara jest czuła na całe spektrum widma, daje jednak dość niskie napięcie i należałoby stosować ją ze wzmacniaczem.
2. Fotodioda krzemowa najlepiej odbiera fale nie przekraczające 1,2 μm daje napięcie wyższe od termopary lecz niższe od diody germanowej.
3. Fotodioda germanowa pokrywa podobnie jak termopara całe spektrum widma, ich charakterystyki są zbliżone do siebie.
λ [μm] |
termopara U [mV] |
fotodioda Si U[mV] |
fotodioda Ge U [mV] |
0,6 |
0,07 |
2,3 |
23 |
0,7 |
0,14 |
4,9 |
43 |
0,8 |
0,2 |
6,8 |
59 |
0,9 |
0,3 |
8,3 |
79,8 |
1 |
0,5 |
6,4 |
105 |
1,1 |
0,6 |
2,1 |
113 |
1,2 |
0,64 |
0,4 |
116 |
1,3 |
0,59 |
0,2 |
118 |
1,4 |
0,37 |
0,2 |
107 |
1,5 |
0,44 |
0 |
115 |
1,6 |
0,4 |
0 |
108 |
1,7 |
0,33 |
0 |
87 |
1,8 |
0,26 |
0 |
64 |
1,9 |
0,18 |
0 |
24 |
2 |
0,15 |
0 |
2 |
1
Wyszukiwarka
Podobne podstrony:
fizyka sprawozdania, widmo absorpcyjne, Piotr Piłaciński
fizyka sprawozdania, widmo absorpcyjne, Piotr Piłaciński
FIZLAB, FIZII 1, +Piłaciński
13 programowalny kontroler przerwan 8259
CW 06 B przerw
ADA wyjatki przerw3
przerwania urz peryf
Twórczość Kazimierza Przerwy -Tetmajera, Szkoła, Język polski, Wypracowania
Jak przerwać wykonywanie pętli (for, PHP Skrypty
E2p, UTP-ATR, Elektrotechnika i elektronika dr. Piotr Kolber, sprawozdania
przerwa
przerwan
111-4, materiały studia, 111. WYZNACZANIE SZEROKOŚCI PRZERWY ENERGETYCZNEJ W PÓŁPRZEWODNIKU METODĄ T
kospekt12, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 12 Wyznaczanie
LAB1, Fizyka laborki, Fizyka (laby i inne), FizLab, fizlab, 001 WA~1
PRZERWANIE CIĄŻY DO 9 TYGODNIA, Wszechnica Świętokrzyska, praca, seminarium
więcej podobnych podstron