Statystyka i demografia
STATYSTYKA:
Statystyka - zajmuje się poznawaniem i opisem zjawisk i procesów , które rejestrowane są w skali masowej.
Cechy możemy podzielić na jakościowe ( wariant cechy niemierzalnej ) i ilościowe na : ciągłe - np. przy wzroście i wadze mogą występować warianty nie odpowiadające pełnym kilogramom czy centymetrom ; skokowe - jej kolejne warianty nie mogą przybierać pośrednich czy ułamkowych , muszą to być np.. liczba pięter w budynku , liczba osób zatrudnionych na stałe.
Szereg statystyczny - jest to liczbowe ujęcie poddanej zbiorowości badaniu wg określonego kryterium . Kryterium stanowi wybrana cecha i jej warianty.
Dla cech i zjawisk ciągłych występują przedziały 0-10;10-20;20-30 ( 10 lat zaliczamy do przedziału drugiego )
Dla cech skokowych przedziały 0-9;10-19;20-29.
Średnia arytmetyczna - aby ją otrzymać należy dodać wszystkie indywidualne wartości cechy mierzalnej posiadane przez poszczególne jednostki danej zbiorowości i ogólną sumę podzielić przez liczbę objętych badaniem jednostek statystycznych .
Statystyka
Opisowa,
Matematyczna - wnioskowanie statystyczne.
Statystyka nauka, która w obrębie prób statystycznych pozwala wnioskować jak ta duża grupa będzie funkcjonować w populacjach.
Badanie prowadzi się w próbach i dokonuje się opisu faktu w małych próbach.
Co jest istotą badania, kwestia względna a co jednostką? np. grupa zawodowa, społeczność lokalna.
Co jest badane?- Cechy, własności, indywidualne cechy, które można zmierzyć to cechy mierzalne.
Cechy jakościowe o charakterze okolicznościowym np. kolor włosów, oczu..
Cechy o charakterze binarnym- dychotomicznym- tzn. badamy takie własności, które z góry zakładają dwa warianty. Analiza problemu posiadania dzieci nie pytamy ile tylko posiada lub nie. Posiadanie danej cechy to 1 a jej brak to 0.
Aspekt jakościowy bada czy ma się taki a nie inny stan cywilny, mieszka tu czy tam.
Częstość występowania cechy: własności
Zasady gromadzenia informacji (sposoby).
Szereg prosty- praktykowany w określonym kontekście próba wynosi 10 osób.
Szereg rozdzielczy- przy większej próbie.
xi - Własność cechy poddanej badaniu
ni - częstotliwość występowania danej cechy w analizowanej zbiorowości
xi ni
160 5
161 10
162
,,
Uzupełniająca wersja to szereg rozdzielczy przedziału i szereg prosty zamiennie.
Badamy wzrost
Xi zakres ni ilość
150 - 160 20
160 - 170 30
170 - 180 40
180 - 200 50
>200
Gdy nie ma sztywnego przyporządkowania granicy- nie piszemy 150 -160- >160 liczę do 160.
Otwartą strukturę możemy stosować do górnej granicy >200
Osobnik o 170 cm, do której grupy? Cecha ilościowa o charakterze ciągłym.
Cecha ilościowa o charakterze skokowym.
W cechach ilościowych wyróżniamy cechy o charakterze ciągłym i skokowym.
Co jest podstawą rozróżnienia?:
Wzrost (ilościowa i mierzalna) charakter ciągły,
Dzieci (ilościowa i mierzalna) skokowy, kwoty całkowite.
do 160 - tutaj klasyfikujemy sytuację, które nie osiągnęły 160,
160 -170 - tutaj otwarty dla 160(dalszy przedział do góry).
170 przedział powyżej 170
Cechy jakościowe mierzalne i ilościowe łącznikiem są cechy binarne
posiadanie własności kod 1, lub jej brak kod 0.
O szeregu klasycznym lub przedziałowym decyduje, co jest badane.
Czy warto redukować liczbę przedziałów czy zostawić bardzo zróżnicowane zasoby?
Najistotniejszą miara statystycznego opisu jest kwestia wielkości średniej, przeciętnej miary statystycznej.
W badaniach statystycznych badane są próby a nie całe reprezentacje.
Relatywność próby badanej, aby poprawnie mówić o populacji badanie powinno być przeprowadzone w próbie reprezentatywnej.
Próba reprezentatywna
Charakterze ilościowym,
O charakterze jakościowym dotyczy jak duża powinna być próba badawcza np. wzrost
Udział próby w stosunku do populacji. Jakość - próba liczna, próba równa populacji.
Jakie elementy poddawane są badaniom i jakie podlegają statystycznemu opisowi?
Cechy, własności np. struktura wykształcenia, dochody.
Analizowanie procesów demograficznych produkcyjnych.
Techniki miar - średnia arytmetyczna, przeciętna np. wzrost dochodu
Σxi - suma obserwowanych wielkości
X =
Σ ni - suma obiektów badanych (rozdzielczy klasyczny)
Σxi • ni
X =
Σ ni
Jak liczymy algorytmy- szereg rozdzielczy klasowy (przedziały)
xi ni xi
160 20 155 gdy nieliczna grupa
160-170 30 165
170-180 40 175
200
wybieramy środek przedziału, gdy nieliczna grupa
Σxi • ni
X =
Σ ni xi środek przedziału klasowego
możemy odejść od wiarygodności, dla otwartych przedziałów 200 >
DEMOGRAFIA
Dyscyplina naukowa, która zajmuje się badaniem i prognozowaniem zjawisk związanych
z liczebnością określonych populacji.
Szczególne zainteresowania badawcze to:
zmiana liczby ludności.
opisywanie wyników badań, które bezpośrednio i pośrednio warunkują zmiany liczby ludności,
badanie struktur ludnościowych ze względu na cechy demograficzne.
Co kształtuje ruch naturalny? (saldo)
Ruch naturalny kształtują dwa zjawiska takie jak
urodzenia,
zgony.
Ostatnie dwa lata w Polsce jest więcej zgonów niż urodzeń. Przyrost ludności następuje z powodu migracji ludności.
Co powoduje migrację?
- praca
- mieszkanie
- status materialny
Apogeum migracji to lata 50 (remanenty powojenne).
Migracje ekonomiczne lata 70 (główny kierunek to ze wsi do miast, Katowice mężczyźni Łódź kobiety). Najsłabiej reprezentowany kierunek to miasto wieś.
Dzisiaj dominujący kierunek to ze wsi do miasta.
Badanie struktur ludnościowych ze względu na cechy demograficzne.
Cechy demograficzne to
płeć,
wiek,
stan cywilny,
małżeństwo (nawiązywanie i rozwiązywanie),
dzietność,
analiza wieku produkcyjnego.
Obserwujemy sygnały opóźnienia rozwoju
- rodność przesuwa się z wieku 23 do 27 lat,
spada ilość dzieci - 1,25,
liczba rozwodów jest większa od liczby zawieranych związków.
Proces defeminizacji zmienny. Zmienność wynika z faktu, że od dawna rodzi się więcej chłopców niż dziewczyn 110 : 112. W skali globalnej nadwyżka ta jest obniżona do 105 dla dziewczyn. Bierze się stąd, że w młodszych kategoriach dominuje płeć męska a w starszych żeńska (stare baby). Powyżej 70 lat na 300 kobiet przypada100 mężczyzn.
Decyduje przeciętna długość życia, średnia mężczyzn jest niska. Jeżeli tendencje dążenia do długości życia utrzymają się na dotychczasowym poziomie to populacja ludzi będzie starsza.
Polskie społeczeństwo jest sfeminizowane jak w skali globalnej, jednak do 35 roku życia dominują mężczyźni od 35 kobiety (jaskrawo widoczne w starszych kategoriach wiekowych).
Tendencja zmierza do, maskumilizacji czyli defeminizacji.
wyż demograficzny
po II wojnie światowej
lata 1946 - 48
Polskie społeczeństwo starzeje się, długość życia przedłuża się obecnie do 75 lat.
W Polsce maleje udział ludzi młodych, wzrasta udział ludzi w wieku średnim i starym, przyjmuje się starość demograficzna to bariera 65 lat.
Miara średnia: miara przeciętna - granica wiekowa nadwyżki mężczyzn nad kobietami to
35 rok życia - miasto 40 lat, wieś 30 lat.
Wartość średniej można uzyskać z różnych elementów: np. 100 zł. Podwyżka albo wszyscy, albo jeden zero a drugi 200 zł.
Średnia przeciętna to miara uniwersalna, felerna - miara subiektywna przy pytaniu o zróżnicowanie podwyżki, gdy jest, że każdy po 100 zło to zróżnicowania nie ma, gdy nie każdy to odchylenie jest np. przy odchyleniu 300% będą duże różnice.
Zróżnicowanie obserwacji
Miara zróżnicowania obserwacji jest, konieczność udzielenia odpowiedzi czy badana zbiorowość jest jednorodna nie zróżnicowana, taka sama z punktu badań, czy też jest niejednorodna. Jeśli jest zróżnicowana to jaka jest skala odmienności czy różnorodności.
Podstawową miarą służącą do określenia stopnia zróżnicowania obserwacji jest wariancja
Jest to wyznaczenia odchylenia standardowego.
Odchylenie standardowe oznaczamy symbolem, literą „S”
S = 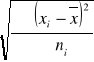
xi - obserwacja,
ni - ile liczy próba,
x - średni wzrost
Istota polega na tym aby określić o ile konkretne obserwacje odstają od rzeczywistości
Aby uwidocznić odchylenie - lub + to podnosimy do kwadratu
Powyższy wzór adekwatny dla szeregu prostego.
Przy szeregu rozdzielnym
S = 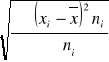
Im większa wartość odchylenia tym większe zróżnicowanie ludności. Jeżeli odchylenie standardowe wynosi S = 0 to zbiorowość jest jednorodna, występuje brak różnic między badanymi obiektami
Badanie dotyczące wzrostu przeprowadzimy w grupie z 2 podgrupami.
Panowie Panie
XΔ = 175cm Xo = 168
SΔ = 6cm So = 5cm
Generalnie mężczyźni więksi, ale kto ma większe zróżnicowanie
Wskaźnik zmienności V
Wskaźnik zmienności V = ![]()
Vk = 5/168 = 0,029 2,9%
Vm = 6/175 = 0,034 3,4%
Wskaźnik zmienności mnożymy przez 100 uzyskujemy wynik w %.
Kobiety bardziej się koncentrują przy 168 cm a mężczyźni bardziej zróżnicowani.
Badanie dynamiki to ocena skali oraz kierunku występowania zmian badanych faktów.
Fakty mogą mieć różny charakter demograficzny np. siła i kierunek zmian ludności, przyrost liczby ludności, ubytek. Jak wielka jest skala zmian, w którą stronę?
Najprostsza techniką wyliczenia różnicy?
Po wyliczeniu uzyskujemy wartość
- liczba mniejsza lub
+ liczba większa
o skali decyduje konkretna wartość o tyle osób mniej lub więcej.
Informacje uzyskane są wiarygodne, ( gdy nie popełniono błędu).
Przyrost o 60 osób w trzech horyzontach czasowych, jaka to dynamika?
I 60 osób populacja 1000 osób,
II 60 osób populacja 1060,
III 60 osób populacja 1120.
Dynamika wzrostu maleje w horyzoncie czasowym użyteczność miary jest ograniczona.
Drugi aspekt to brak użyteczności.
Czy dynamika zmian miasta Piły jest zbieżna z dynamiką miasta Poznań?
Piła 60 osób Poznań 300 osób
Jeżeli chcemy rozpatrywać pewne fakty w ujęciu dynamicznym a uzyskane wyniki wykorzystać dla porównań czasowych lub rodzajowych należy stosować miary względne.
Zmiany bezwzględne to różnica pomiędzy
Yt1 - Yt0 różnica pomiędzy rokiem 2000 a 2001
Y - fakt poddany badaniu (liczba ludności),
t - zakres czasowy natężenie zjawiska,
t0 - 2000 rok
t1 - 2001 rok
Miary
Stopa przyrostu (stopa ubytku)
Wylicza się z formuły generalnej, różnica do wielkości wyjściowej, wynik obrazuje skalę zmian.
Yt1 - Yt0
= ![]()
stopa zmian, wynik zastosowania formuły może dać odpowiedź
Yt0 na pytanie, jaka jest skala i kierunek zmian.
Alternatywnym, uzupełniającym podejściem jest indeks
istotą jego stosowania jest stopa zmian.
Formuły najczęściej stosowane
indeks jednopodstawowy
indeks łańcuchowy.
Indeks = Yt1/Yt2
Yt1 - późniejszy
Yt2 - wcześniejszy
Sposób liczenia obu indeksów jest taki sam.
T Y
-
-
-
-
-
-
Indeks dynamiki jednopodstawowej jedna podstawa stała
91/90 =
92/90 =
93/90 =
Indeks dynamiki łańcuchowej fakt bezpośrednio poprzedzający
91/90 =
92/91 =
93/92 =
Wynik mniejszy niż 1 to ubytek ludności, teoretycznie można otrzymać wynik „0”,
górnej granicy nie jesteśmy w stanie określić.
Uzyskany wynik można zapisać w procentach, wynik mnożymy przez 100%.
Yt1/Yt2 = ...... x 100% = ...... %
Rezultat, 1.12 czyli 112% stwierdzamy przyrost o 12%
112% tzn., że liczba ludności miasta Piły w 1991 r stanowiła 112%
względem 100% w roku 1990, albo stwierdzamy przyrost o 12% (skala zmiany).
95% ubytek ludnościowy, skala ubytku 5%, albo liczba ludności miasta Piły w 1991
stanowi 95% w stosunku do 100 % w roku 1990
Interpretacje dotyczą obu indeksów.
Produkt krajowy brutto PKB w naszym kraju;
pojęcie bezwzględne w złotych
w pojęciu względnym w procentach np. 2,5-3%
Dynamika skali
To ciągły wzrost, ale może też zaistnieć falowość ruchu (recesja).
Pytanie, czy zaszły zmiany, jeżeli tak to jakie?
Jak kształtowała się liczba ludności w 2000 roku względem 1990 ?
Indeks dynamiki podstawowej w obu przypadkach taki sam.
Miasto A = 112 %, miasto B = 112%
liczba
ludności A
B amplituda
t
1990 2000
ampl. czasowa
W tej sytuacji nie rozpatrujemy dynamiki w latach 1990-2000 ale w poszczególnych okresach i mimo stałego wzrostu (wartość stała) mamy różną charakterystykę,
miasto „B” bardziej zróżnicowane.
Która amplituda jest bardziej dynamiczna?.
Natężenie zjawiska-
To jaki jest kierunek, wzrost i ubytek, np. feminizacja i maskulizacja .
Wskaźnik tempa zmian
Liczba ludności - dynamika wzrostu.
Po zastosowaniu tej formuły otrzymamy wielkość niemianowaną, może pojawić się problem interpretacji. Wynik, wskaźnik mnożymy przez 100% i otrzymujemy wskaźnik procentowy, informację o ile procent wyższy lub niższy jest poziom badanego zjawiska względem punktu odniesienia, który przyjmujemy za 100%.
Y1 - Y0
ΔY = x 100%
Y0
Jeżeli uzyskamy wartość wskaźnika 100% oznacza to brak zmian. Jeżeli wielkość 100% jest punktem odniesienia, to 109% świadczy o przyroście wskaźnika. Skalę wzrostu oznaczamy w % względem punktu odniesienia, a więc przyrost o 9%.
Inna interpretacja.
Można powiedzieć, że liczba ludności w okresie Y1 wynosiła 109% liczby Y0.
Może zdarzyć się, że otrzymamy wynik 93% świadczy to o zmniejszeniu się liczby ludności np. o 7% lub stanowi 93% liczby ludności z okresu Y0.
Jest to wskaźnik jedno podstawowy
Można wyrazić go również w inny sposób
Y2 - Y1
Y1
lub zastosować indeks
Y1
ΔY = x 100%
Y0
Jest to sytuacja prostsza, liczbę ludności z okresu „ 1 ” odnosimy do okresu „ 0 ”
Wynik otrzymujemy taki sam.
Trend czasowy.
Jest to zagadnienie zmierzające do tego aby obserwowanym zmieniającym się wartościom przypisać matematyczną postać funkcji, która określi przeciętną skalę zmian warunkowaną upływającym czasem.
Aby dokonać oszacowania tej funkcji musimy dysponować dwiema informacjami;
czas
informacja.
t y
1990 1 liczba ludności
2
3 ![]()
= ao ± a1t
4
5
6
7 ![]()
= 38 500 + 1,3 t
8
9
10
ao - bazowa liczba ludności
a1 - kierunek i tempo zmian
![]()
- wartość teoretyczna
y - liczba ludności
y - średnia arytmetyczna ludności
t - seria czasowa
![]()
= ao ± a1t
Parametr a1 odgrywa największe znaczenie
Np. próba wyliczenia liczby ludności jaka będzie się kształtować na przestrzeni 10-lecia, liczbę ludności określić można;
w tysiącach osób
w milionach osób
lub w innych jednostkach
Kwestia jednostki w obliczeniach odgrywa znaczącą rolę
![]()
= 38 500 + 1,3 t - w tysiącach osób
Jeżeli parametr „a1” jest dodatni to znaczy że zjawisko „![]()
” wykazywało tendencję przyrostową. Jeżeli ujemny mamy wówczas tendencję spadkową.
Parametr ten w tym przypadku 1,3 odnosi się do wzrostu o 1300 osób.
Interpretacja
Liczba ludności Polski w okresie 1990-1999 wykazywała tendencję wzrostową o przeciętnym natężeniu 1.3 tysiąca osób w skali roku.
Taką formułę możemy wykorzystać do prognozowania.
Parametry takie mogą jednak być obarczone błędem.
W czasie zmienia się parametr 1,3 ponieważ
zmniejszyła się rodność
zmniejsza lub zwiększa się długość życia
zmieniają się warunki ekonomiczne
występuje migracja ludności
Sprawdzenie wiarygodności.
Łańcuch zmian ludności.
y y
+1
-1
+2
-1
+3
-3
Polska t t
przebieg rzeczywisty
stały wzrost
Często zjawiska przyjmują kształt oscylacyjny, sezonowy. Nie daje to żadnego użytku, ponieważ nie można wyciągnąć wniosków.
Poziom faktyczny można porównać z teoretycznym.
t y ![]()
1990 1 - -
2 - -
3 - -
4 - -
-
-
-
-
-
1990 10 -
Korelacja,
jest to współwystępowanie, Muszą występować przynajmniej dwa elementy
jeden to „x”
drugi to „y”.
Korelacja - ( teoria współzależności ) wahania w jednym zjawisku wywołują tendencje odpowiedniego kształtowania w drugim zjawisku. Może między nimi zachodzić relacja przyczynowo skutkowa - współzależność.
Jednostronna - np. plon ziemniaka y, stopień nawożenia x ( wysokość plonu zależy od stopnia nawożenia , ale stopień nawożenia nie zależy od plonu )
Dwustronna - x powoduje y i y powoduje x ( x - poziom produkcji , y - wydajność pracy )
Między badanymi cechami mogą występować relacje przyczynowo skutkowe, lub sytuacje w których nie odnajdujemy logicznego, przyczynowego faktu zależności a mimo to cechy te mogą współwystępować - być ze sobą skorelowane. W zależności od tego czy występuje skutek czy nie, chcemy wiedzieć czy cechy te są współzależne. Instrumentem tym jest regresja. Miernikiem który obrazuje współwystępowanie jest współczynnik korelacji.
Według PEARSON`a istnieje pewna grupa współczynników korelacji. Poprzestaniemy na współczynniku korelacji prostoliniowej.
x y zapis symboliczny ![]()
kierunek współwystępowania
siła współwystępowania
O kierunku informuje znak ![]()
oraz o sile współczynnika liczba w przedziale zamkniętym od -1 do + 1 ![]()
.
Jeżeli współczynnik korelacji przyjmie wartości ujemne
Przykład:
x - liczba lat
y - częstotliwości kontaktów seksualnych
interpretacja
gdy x rośnie
y maleje współczynnik maleje
gdy x rośnie
y rośnie współczynnik rośnie
gdy x maleje
y maleje współczynnik rośnie
Jeżeli nie popełnimy błędów rachunkowych to wartość współczynnika korelacji zamyka się w przedziale zamkniętym od -1 do + 1 ![]()
.
y
korelacja dodatnia
2 z połączenia punktów powstaje linia prosta
o nachyleniu 45 stopni
1
0 1 2 x
Wykres przy wartości współczynnika korelacji + 1.
Kiedy wzrostowi cechy „x” o jedną jednostkę obserwacji odpowiada wzrost cechy „y” także o jedną jednostkę obserwacji
y korelacja ujemna
x
Współczynnik korelacji - 1.
Kiedy spadkowi cechy „x” o jedną jednostkę odpowiada spadek cechy „y” też o jedną jednostkę obserwacji.
y współwystępowanie
przy braku powiązania
x
Realizacji cechy „x” nie odpowiada niezmienna „y” lub na odwrót.
y
Wartości inne pomiędzy
„0” a „+1”
„0” a „-1”
x
Siła korelacji
Być może trzeba będzie ukształtować cechy według siły występowania. Np.
![]()
współwystępowanie
0,8 2
-0,9 1
0,5 3
-0,4 4
0,2 5
0 6
O sile korelacji decyduje wartość bezwzględna, bez znaku + bądź -.
„0” oznacza brak współwystępowania, współwystępowanie nie zachodzi.
Przy wyznaczaniu współczynnika korelacji musimy mieć informację cechy „x” i „y”.
Współczynnik korelacji rang wg SPERMAN`a.
Mamy uporządkowany układ 2 cech np. od najwyższych do najniższych. Do określenia korelacji bierzemy pod uwagę zajmowane miejsce.
Nr 1. Pierwsze miejsce
itd.
Badamy czy ranga pierwszego miejsca odpowiada koreluje z cechą z następnego miejsca.
Współczynnik korelacji rang mieści się również w przedziale - 1 do + 1.
Np. współwystępowanie,
Współczynnik korelacji
M - 0,75
K - 0.70
Który współczynnik jest bardziej wiarygodny.
Wynik jest bardziej wiarygodny wówczas gdy badania przeprowadza się na większej liczbie osób.
Współwystępowanie.
Miara stosowana we wszystkich sytuacjach gdy mamy do czynienia z dwiema cechami. Analizujemy cechy ilościowe. Nie istnieją żadne cechy ograniczające porównywanie, można poddać kojarzeniu różne również abstrakcyjne sytuacje.
Regresja
Jest to funkcja prostoliniowa lub krzywa, która obrazuje wzajemne zależności miedzy dwoma badanymi cechami, zjawiskami. Charakter tej zależności sprowadza się do wskazania jaki jest wpływ wartości jednej z cech na kształtowanie się wartości drugiej cechy drugiego zjawiska.
Analizę regresji można przeprowadzać w zależnościach prosto i krzywoliniowych.
y y
lub
x x
Wykres regresji krzywoliniowej, prostoliniowej
Przykład.
Liczba dojeżdżających do pracy w zależności od odległości.
Im bliżej do danego ośrodka, tym większa liczba dojeżdżających i na odwrót.
Jeżeli współczynnik korelacji wyniesie „0” to mamy informację, że zależności nie występują. Jeżeli natomiast występuje wielkość ± do 1 to znaczy, że zależności występują. W jaki sposób jedna cecha oddziałuje na drugą?
Cechy
Zmienna zależna - jest ona zależna, obrazuje jaką własność będziemy analizowali.
Np. liczba dojeżdżających do pracy zależy od ..., liczba ocen zleży .....
Wskazujemy od czego zależy, zależy od cechy niezależnej.
Zmienna niezależna - to cecha która wpływa, warunkuje wielkość cechy zależnej zmiennej.
Zmienna zależna oznaczana jest literą „y”.
Zmienna niezależna oznaczana jest literą „x”
Analiza regresji rozpatruje zależności typu przyczynowo-skutkowego
przyczyna (zmienna niezależna „x”)
skutek (zmienna zależna „y”)
Funkcja regresji i jej zapis.
Istnieje
regresja wielo zmienna, kiedy występuje więcej niż jedna zmienna niezależna,
regresja jedno zmienna, kiedy występuje jedna cecha niezależna „x”.
W regresji jedno cechowej występuje jeden „x” jedna niezależna. Natomiast w wielo zmiennej, wiele niezależnych.
y = ± ax + b
y y
x x
„y” - zmienna zależna
„a” - współczynnik kierunkowy - posiada wielkość „+” bądź „-„ określa jaki jest wpływ
co do kierunku i co do skali.
„b” - parametr korygujący, wyraz wolny, tylko w znaczeniu graficznym
Jaki jest wpływ parametru „a” cechy zmiennej „x” na wartość zmiennej zależnej „y”.
Jeżeli będzie ujemny (-) to wzrostowi „x” odpowiadać będzie zmniejszenie „y”.
(Wraz ze wzrostem odległości maleje liczba dojeżdżających do pracy).
Jeżeli parametr jest wartością (+) wówczas wzrostowi cechy „x”
odpowiada wzrost cechy „y”.
Np. Od czego może zależeć cecha - ilość dzieci w rodzinie.
Jak zmieni się ilość dzieci w rodzinie gdy przychód zwiększy się o jedną jednostkę.
W wyniku przeprowadzonego badania uzyskaliśmy model reprezentacyjny
y = -0.25 x +1
y - ilość osób
x - przychód w tys. zł na osobę w rodzinie.
Jeżeli stopa życiowa „x” wzrośnie o jednostkę pomiaru, czyli o 1 tysiąc zł. na osobę,
to liczba dzieci w rodzinie zmniejszy się o 0,25 osoby.
Gdy stopa życiowa rośnie to przyrost naturalny maleje.
Parametr „b” to nic innego jak wartość zmiennej zależnej „y” dla sytuacji w której wartość „x” wartość cechy niezależnej ukształtuje się na poziomie przy „x” równym „0” (zero).
Metoda najmniejszych kwadratów - liczenie parametrów funkcji regresji.
y
x
Wiarygodność tej funkcji regresji jest większa przy mniejszym rozproszeniu punktów pomiaru, odniesienia.
..................................................................................
Egzamin
Nie będzie wzorów i obliczeń.
Mogą być podane liczby obrazujące współczynniki np.
korelacji w celu zweryfikowania np. „ 0 ± 1 ”
uszeregowanie ze względu na siłę korelacji (wartości bezwzględne)
ustawienie współczynników ze względu na kierunek
funkcja regresji, dokonanie interpretacji zapisu, wielkości jednostki
dynamika, analiza jak zmieniają się wielkości, tempo, indeks
średnia arytmetyczna (symetryczna i asymetryczna) ograniczenia
asymetria - rozkład symetryczny, asymetryczny, konsekwencje
zróżnicowanie obserwacji
natężenie obserwacji - siła zróżnicowania, stopień zróżnicowania, odchylenie standardowe
wskaźnik zmienności.
Wyszukiwarka
Podobne podstrony:
zadanie o analizie struktury, statystyka i demografia-Hnatyszyn-Dzikowska ćwiczenia
Statysta kolokwium ubiegly, Stosunki międzynarodowe - materiały, II semestr, Statystyka i demografia
STATYSTYKA- ściąga, statystyka z demografią
statystyka zadanie, statystyka i demografia-Hnatyszyn-Dzikowska ćwiczenia
Praca zaliczeniowa ze statystyki i demografii
Przykład na zajęcia ze statystyki1, Politologia, Statystyka i demografia
Statystyka i demografia, STATYSTYKA-zadania(interpretacje), ZADANIE
Statystyka i demografia Regresja liniowa 2011 2012 Kubiczek
Statystyka i demografia, tabelka, Lp
ZAKRES MATERIAŁU OBOWIĄZUJĄCEGO NA EGZAMINIE ZE STATYSTYKI Z DEMOGRAFIĄ, statystyka z demografią
Przykład 0, Politologia, Statystyka i demografia
cwiczenia demografia 1, III semestr, statystyka i demografia
statystyka esej małżeństwa, statystyka i demografia-Hnatyszyn-Dzikowska ćwiczenia
Statystyka i demografia 1
4. Materiały do ćwiczeń ze statystyki z demografią, statystyka z demografią
Demografia, SZKOŁA, STATYSTYKA I DEMOGRAFIA
oceny statystyka gr 2, III semestr, statystyka i demografia
wyklad 2 statystyka i demografia administracja zaoczne, Statystyka
3. Materiały do ćwiczeń ze statystyki z demografią, statystyka z demografią
więcej podobnych podstron