Politechnika Wrocławska
INSTYTUT FIZYKI |
Sprawozdanie z ćwiczenia nr 44. |
Klaudiusz Fatla
|
Temat:
Badanie zależności rezystancji od temperatury dla metali i półprzewodników. |
WYDZIAŁ ELEKTRYCZNY, rok II |
Data: Ocena: 20 - 11 - 96 |
1. Zakres ćwiczenia :
Celem ćwiczenia był pomiar zależności rezystancji metalu i półprzewodnika w zależności od temperatury w zakresie od temperatury pokojowej do około 370 K, wyznaczenie współczynnika temperaturowego rezystancji oraz szerokości pasma wzbronionego w półprzewodniku.
2. Wiadomości ogólne :
W metalach swobodnymi nośnikami ładunku są elektrony z niezapełnionego pasma przenoszenia i konduktywność wyraża się wzorem:
n - koncentracja swobodnych nośników ładunku
un - ruchliwość swobodnych nośników ładunku
.
W metalach koncentracja swobodnych nośników ładunku nie zależy od temperatury, a ruchliwość ich ustala się w warunkach równowagi, gdy średni przyrost prędkości unoszenia (vn) wywołany działaniem sił pola elektrycznego (E), jest równoważony ubytkiem tej prędkości. W metalach istnieją dwa podstawowe mechanizmy rozpraszania. W wysokich temperaturach głównym mechanizmem są drgania cieplne atomów w węzłach sieci krystalicznej. Drgania te powodują niejednorodność gęstości (fluktuacje gęstości), na której rozprasza się fala. Rozpraszanie elektronów polega na zderzeniach ich z fononami. Ze wzrostem temperatury zwiększa się amplituda drgań sieci i przekrój czynny na rozpraszanie, więc maleje ruchliwość i konduktancja, wynikiem czego jest wzrost rezystancji. Dla temperatur wysokich i dla małozanieczyszczonych metali jednoskładnikowych istnieje (w przybliżeniu) liniowa zależność między przyrostem rezystancji metali a przyrostem temperatury. Związek ten ma postać:
R0 - rezystancja w 0*C
Rt - rezystancja w t*C
α0 - współczynnik temperaturowy rezystancji od 0*C do t*C.
W praktyce temperaturą odniesienia jest t = 20*C, więc:
.
Drugim mechanizmem rozpraszania są defekty sieci krystalicznej. Jest on dominujący w niskich temperaturach dla metali jednoskładnikowych. Składowa rezystancji Ri (rezystancja resztkowa - na defektach sieci) jest niezależna od temperatury i mała w porównaniu ze składową rezystancji Rl, spowodowana drganiami sieci w temperaturze pokojowej (20*C). Obydwa czynniki rezystancji są addytywne:
.
Mechanizm rozpraszania swobodnych nośników ładunku w półprzewodnikach jest zbliżony do tego z metali, z tym że w półprzewodniku głównymi defektami strukturalnymi, które decydują o rozpraszaniu w niskich temperaturach, są zjonizowane atomy domieszek. Dla półprzewodnika, w zakresie temperatur przewodnictwa samoistnego, mierząc zależność rezystancji od temperatury można wyznaczyć szerokość pasma wzbronionego Eg. Rezystancję w zakresie samoistnym możemy opisać równaniem:
skąd
gdzie ln R1, 1000/T1 i ln R2, 1000/T2 oznaczają współrzędne punktów na początku i końcu prostoliniowego odcinka wykresu ln R = f(1000/T).
3. Spis przyrządów .
- dwa multimetry cyfrowe typu 1321 o dokładności * (0,2% wartości mierzonej + 0,1% podzakresu)
- termometr rtęciowy z podziałką elementarną 1*, dokładność pomiaru * 0,5*C
4. Wyniki pomiarów :
Tab. 1. Pomiar temperatury i rezystancji dla rezystora platynowego.
Lp. |
T [°C] |
RPt [Ω] |
ΔRPt [Ω] |
α [1/K] |
Δα [1/K] |
1 |
23,0 |
1103,0 |
4,2 |
- |
- |
2 |
28,0 |
1124,0 |
4,3 |
3808*10-6 |
7*10-6 |
3 |
33,0 |
1141,0 |
4,3 |
3445*10-6 |
7*10-6 |
4 |
38,0 |
1176,0 |
4,4 |
4412*10-6 |
7*10-6 |
5 |
43,0 |
1190,0 |
4,4 |
3944*10-6 |
7*10-6 |
6 |
48,0 |
1213,0 |
4,4 |
3989*10-6 |
7*10-6 |
7 |
53,0 |
1233,0 |
4,5 |
3929*10-6 |
7*10-6 |
8 |
58,0 |
1251,0 |
4,5 |
3834*10-6 |
7*10-6 |
9 |
63,0 |
1270,0 |
4,6 |
3785*10-6 |
7*10-6 |
10 |
68,0 |
1296,0 |
4,6 |
3888*10-6 |
7*10-6 |
11 |
73,0 |
1315 |
5 |
3844*10-6 |
7*10-6 |
12 |
78,0 |
1336 |
5 |
3841*10-6 |
7*10-6 |
13 |
83,0 |
1356 |
5 |
3823*10-6 |
7*10-6 |
14 |
88,0 |
1376 |
5 |
3808*10-6 |
7*10-6 |
15 |
83,0 |
1344 |
5 |
3903*10-6 |
7*10-6 |
16 |
78,0 |
1324 |
5 |
3924*10-6 |
7*10-6 |
17 |
73,0 |
1302 |
5 |
3912*10-6 |
7*10-6 |
18 |
68,0 |
1281,0 |
4,6 |
3918*10-6 |
7*10-6 |
19 |
63,0 |
1258,0 |
4,5 |
3880*10-6 |
7*10-6 |
20 |
58,0 |
1241,0 |
4,5 |
3988*10-6 |
7*10-6 |
21 |
53,0 |
1206,0 |
4,5 |
3581*10-6 |
7*10-6 |
22 |
48,0 |
1176,0 |
4,4 |
3196*10-6 |
7*10-6 |
23 |
43,0 |
1159,0 |
4,4 |
3214*10-6 |
7*10-6 |
24 |
38,0 |
1138,0 |
4,3 |
3000*10-6 |
7*10-6 |
25 |
33,0 |
1122,0 |
4,3 |
3030*10-6 |
7*10-6 |
26 |
28,0 |
1105,0 |
4,3 |
2938*10-6 |
7*10-6 |
27 |
23,0 |
1089,0 |
4,2 |
- |
- |
xśr |
- |
- |
- |
375*10-5 |
- |
Δxśr |
- |
- |
- |
7*10-5 |
- |
Pomiary 1*14 dla temperatury rosnącej, pomiary 15*27 dla temperatury malejącej.
α = (3,75 * 0,07)*10-3 [1/K]
Tab. 1. Pomiar temperatury i rezystancji dla rezystora półprzewodnikowego.
Lp. |
T [°C] |
Rpół [kΩ] |
ΔRpół [kΩ] |
1 |
23 |
10,79 |
0,04 |
2 |
28 |
8,50 |
0,04 |
3 |
33 |
6,370 |
0,033 |
4 |
38 |
5,550 |
0,031 |
5 |
43 |
4,46 |
0,03 |
6 |
48 |
3,51 |
0,03 |
7 |
53 |
2,980 |
0,026 |
8 |
58 |
2,380 |
0,025 |
9 |
63 |
1,973 |
0,006 |
10 |
68 |
1,6000 |
0,0052 |
11 |
73 |
1,374 |
0,005 |
12 |
78 |
1,1290 |
0,0043 |
13 |
83 |
0,960 |
0,004 |
14 |
88 |
0,810 |
0,004 |
15 |
83 |
1,0350 |
0,0041 |
16 |
78 |
1,2260 |
0,0045 |
17 |
73 |
1,4600 |
0,005 |
18 |
68 |
1,7480 |
0,006 |
19 |
63 |
2,100 |
0,024 |
20 |
58 |
2,520 |
0,025 |
21 |
53 |
3,580 |
0,028 |
22 |
48 |
4,60 |
0,03 |
23 |
43 |
5,680 |
0,032 |
24 |
38 |
7,400 |
0,035 |
25 |
33 |
8,52 |
0,04 |
26 |
28 |
10,17 |
0,04 |
27 |
23 |
12,030 |
0,045 |
Pomiary 1*14 dla temperatury rosnącej, pomiary 15*27 dla temperatury malejącej.
Szerokość pasma wzbronionego:
Eg1 = 1,224*10-19 J = 0,764 eV,
Eg2 = 1,175*10-19 J = 0,733 eV.
5. Wzory i przykłady obliczeń :
- błąd pomiaru rezystancji miernikiem cyfrowym [Ω]
kl - dokładność wartości mierzonej [%]
klz - klasa zakresu [%]
Rx - wartość zmierzona [Ω]
Z - zakres pomiarowy [Ω]
Ω
- współczynnik rezystancji (temperatura odniesienia 23*C) [1/K]
R23 - rezystancja w 23*C [Ω]
Rt - rezystancja w t*C [Ω]
t - temperatura [*C]
-błąd bezwzględny współczynnika temperaturowego [1/K]
ΔR23 - błąd pomiaru rezystancja w 23*C [Ω]
ΔRt - błąd pomiaru rezystancja w t*C [Ω]
Δ t - błąd pomiaru temperatury [*C]
t - temperatura [*C]
- szerokość pasma wzbronionego
k - stała Boltzmanna, k = 1,38*10-23 [J/K]
R1 - rezystancja półprzewodnika w temperaturze t = 23*C
R2 - rezystancja półprzewodnika w temperaturze t = 88*C
T1 - temperatura t = 23*C
T2 - temperatura t = 88*C
Inne wzory :
- średnia arytmetyczna
n - liczba pomiarów
xj - pomiar j-ty
- średni błąd kwadratowy średniej arytmetycznej (poziom ufności 68,2%)
n - liczba pomiarów
x - średnia arytmetyczna
xj - pomiar j-ty
6. Dyskusja błędów i wnioski :
W doświadczeniu temperaturą odniesienia była t = 23*C, ponieważ taka była temperatura w pomieszczeniu. Współczynnik temperaturowy platyny otrzymany z doświadczenia jest zbliżony, co do wartości, do współczynnika podawanego w tablicach (αPt 20 = 3,9*10-3 [1/K]). Różnice wynikają z różnych temperatur odniesienia . Inne wartości rezystancji otrzymane podczas chłodzenia próbek niż podczas ich ogrzewania mogą wynikać ze zbyt szybkiego schładzania i z niedokładnego odczytu temperatury.
7. Wykresy :
Wyk. 1. Zależność rezystancji platyny od temperatury, R = f(T)
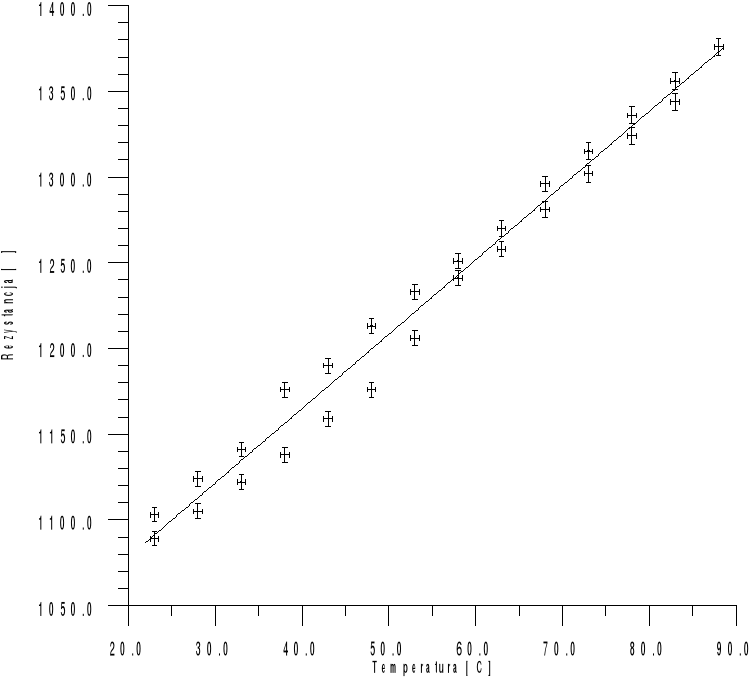
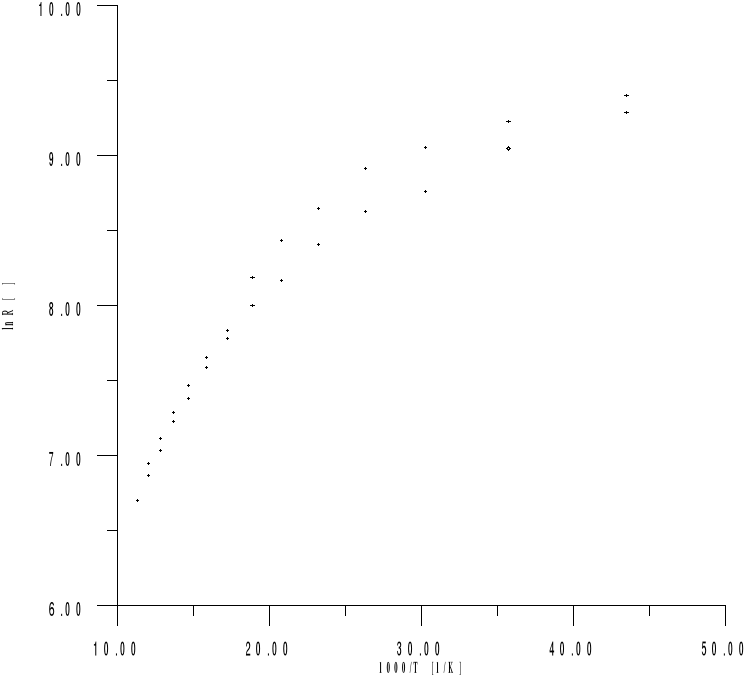
Wyk. 2. Zależność ln R = f(1000/T) dla półprzewodnika.
Wyszukiwarka
Podobne podstrony:
81, Cwiczenie 81 d, Politechnika Wroc?awska
12, Cwiczenie 12 b, POLITECHNIKA WROC?AWSKA
52, Cwiczenie 52 b, Politechnika Wroc˙awska
29, Cwiczenie 29 f, POLITECHNIKA WROC?AWSKA
81, Cwiczenie 81 a, POLITECHNIKA WROC?AWSKA
79, Cwiczenie 79 c, Politechnika Wroc?awska
52, Cwiczenie 52, POLITECHNIKA WROC?AWSKA_
Cwiczenie 30 b, Politechnika Wroc?awska
72, Cwiczenie 72 c, POLITECHNIKA WROC?AWSKA
43, Cwiczenie 43 a, POLITECHNIKA WROC?AWSKA
81, Cwiczenie 81 b, POLITECHNIKA WROC?AWSKA
Cwiczenie 59 c, POLITECHNIKA WROC˙AWSKA
29, Cwiczenie 29 a, POLITECHNIKA WROC?AWSKA
29, Cwiczenie 29 d, POLITECHNIKA WROC?AWSKA
więcej podobnych podstron