Ćwiczenie 8

Badanie procesu zamrażania produktów spożywczych

Wiadomości wstępne

Zamrażanie jest procesem obniżania temperatury produktu poniżej tempera­tury krioskopowej, czemu towarzyszy przemiana fazowa wody w lód. Powsta­wanie lodu wiąże się z koniecznością odprowadzenia znacznych ilości ciepła (około 335,2 kJ/kg), co tłumaczy się zmniejszeniem energii kinetycznej cząste­czek w sztywnej strukturze kryształu w porównaniu z fazą płynną. Ponadto woda przechodząc w lód, zmienia swoje właściwości fizyczne (gęstość, ciepło właści­we, przewodnictwo cieplne, dyfuzyjność cieplną).

Przebieg procesu zamrażania produktów spożywczych

Dla zrozumienia zjawisk zachodzących przy zamrażaniu produktów spożyw­czych mają znaczenie temperaturowe wykresy zamrażania (krzywe mrożenia), podające zależność między czasem a temperaturą w określonym punkcie zamra­żanego ciała. Typowy przebieg procesu zamrażania produktu spożywczego jest pokazany na rysunku 8.1.

Kształt krzywej mrożenia zmienia się w zależności od zastosowanej metody zamrażania, charakteru zamrażanego produktu (wielkość, kształt, skład chemicz­ny, właściwości fizyczne) oraz rodzaju użytego opakowania (lub jego braku). Zależnie od tych czynników krzywa zamrażania staje się bardziej łub mniej

stroma, względnie przesunięta bar­dziej w górę lub w dół. Z przebiegu tej krzywej można określić trzy zasadni­cze odcinki odpowiadające określo­nym etapom procesu zamrażania.

Odcinek a-b krzywej charakte­ryzuje etap schładzania materiału od temperatury początkowej (t_p) do tem- T?° . peratury krioskopowej (4.). Drugi od-

Rysunek 8.1. Krzywa mrożenia produktu (objas- . , , . , .. . , 7 .

nienia w tekście) ^cmek krzywej b-c ilustruje właściwepamrażanie. Zachodzi tu przemiana fazowa wody w lód, w związku z czym temperatura nie ulega widocznej zmianie. W rzeczywistości w miaręJwymrażania ; wody rośnie stężenie roztworu komórkowego i jego punkt krioskopowy stale się lobniża. W miejscu, gdzie krzywa przyjmuje wyraźne strome nachyleni® (punkt c), izaczyna się nowy etap domrażania produktu (termicznej dyfuzji ciepła w zamro­czonym produkcie) zilustrowany odcinkiem c-d. W etapie tym zamrożony produkt obniża swą temperaturę do poziomu założonego w procesie technologicznym. W zasadzie w obrębie odcinka c-d obydwa etapy procesu (właściwe zamrażanie |i domrażanie) przebiegają jednocześnie. W punkcie e produkt osiąga temperaturę gczynnika chłodzącego i proces zamrażania kończy się.

W celu ustalenia momentu zakończenia etapu właściwego zamrażania przyj­muje się punkt f, który leży na przecięciu przedłużenia odcinków b-c i c-d. > Przedłużając analogicznie odcinki a-b i b-c, można określić punkt g charaktery- gzujący rozpoczęcie procesu wymrażania wody. Przeprowadzenie przez punkty f i g prostych prostopadłych do osi odciętych pozwoli znaleźć praktyczny czas właściwego zamrażania próbki (%_p).

Zamrażanie produktów żywnościowych zarówno pochodzenia zwierzęcego, jak i roślinnego przebiega nieco inaczej niż roztworów fizycznych. Wynika to p tkankowej struktury tych produktów - a więc nieciągłej, w której faza płynna Rest uwięziona w ściankach komórek o stałym stanie skupienia. W związku z tym ■proces zamrażania powoduje, oprócz normalnych zjawisk właściwych dla roz- jtworów, także niszczenie struktury tkankowej i zahamowanie przebiegu proce­sów biologicznych. Temperatura krioskopowa, a ściślej mówiąc - początkowa ■temperatura krioskopowa produktów żywnościowych, podobnie jak roztworów Ezycznych, zależy od stężenia ich soku komórkowego, a także od struktury Itkanek, kształtu i wielkości produktu, warunków wymiany ciepła i temperatury ■zamrażania. W związku z tym nie jest ona wartością stałą, ściśle określoną Dla ■większości naturalnych produktów żywnościowych zawiera się w przedziale od PO,5 do -2,0°C.

Z powodu dużej różnicy między właściwościami fizycznymi wody i lodu Łdpowiednie wartości dla produktów zamrożonych i nie zamrożonych znacznie tdbiegają od siebie. Głównym czynnikiem określającym te wielkości jest ilość Rymrożonej wody, którą można obliczyć za pomocą wzoru Raoulta:

; co=l-^ / (8.1)

fedzie: co - udział wody wymrożonej w produkcie [kg/kg]; fe - temperatura feioskopowa produktu [°C]; l_e - średnia końcowa temperatura produktu [°C].

P Korzystając ze wzoru Raoulta, otrzymuje się wyniki przybliżone, ale wy­starczająco dokładne dla praktyki przemysłowej. Wynika z niego, że ilośćwjmmmnmej wody nie zależy od czasu trwania procesu zamrażania, a jedynie od izoacm ej temperatury produktu. Ponadto, w układach biologicznych jest pewna 3ość wody związanej, która nigdy nie wymarza w żadnej temperaturze.

Czas zamrażania

			Wiż
					X
tm					tm
,dQ					dQt
	A
				\	\Ł

Rysunek 8.2. Ochładzanie dwu­stronne płyty nieskończonej (objaś­nienia w tekście)

Najczęściej spotykane kształty oziębianych materiałów to: płyta oziębiana dwustronnie, walec oziębiany na powierzchni bocznej oraz kula i prostopadło­ścian oziębiane ze wszystkich stron.

(8.2)

Zakładając, że płyta nieskończona o grubości / zostaje umieszczona w medium chłodzącym o temperaturze t_m < t_kr (rys. 8.2), z równania Fouriera można określić elementarną ilość ciepła (dQ), jaka odpływa z płyty w czasie dv.

dQ = kFAtd%

Ta sama ilość ciepła jest wydzielana w proce­sie przemiany fazowej, powodując przyrost gru­bości warstwy zamrożonej o dx, czyli:

(8.3)

dQ = q_zp_zFdx

Porównując równania (8.2) i (8.3), otrzymuje się wzór na elementarny czas zamrażania:

4zP

(8.4)

dx =

dx

L JL At I a

gdzie: -jednostkowe ciepło zamarzania produktu [kJ/kg] (tab. 8.1); p_z- gęstość produktu w stanie zamrożonym [kg/m³] (tab. 8.1); a - współczynnik wnikania ciepła od powierzchni produktu do medium [W/(m² • K)] (tab. 8.2); X_e - prze­wodność cieplna właściwa produktu w stanie zamrożonym [W/(m • K)] (tab 8.1); x - grubość warstwy zamrożonej [m]; At = t^ -t_m- czynna różnica temperatury między produktem i medium [°C].

Średnia temperatura medium chłodzącego może być obliczona ze wzoru:

(8.5)

gdzie: t_mp - początkowa temperatura medium [°C] (rys. 8.3); t^ - końcowa temperatura medium [°C] (rys. 8.3).

Tabela 8.1. Właściwości fizyczne niektórych produktów spożywczych (Polley. Snyder, Kotnour: Food Technol., 1980,34(11), s. 76; Gruda, Postolski: Zamrażanie żywności. Wyd. 3, WNT, Warszawa 1999; Stankiewicz: Przemysł Ferm. i Ow.-Warz., 1990, 34(7), s. 17)

	—M	Tempe­	Jedno­	Gęstość		Ciepło właściwe		PrzewoAiość
	Zawar­	ratura	stkowe	[kg/m]		[kJ/(kg • K)]		cieplna właściwa 1
	tość	kriosko­	ciepło					[W/(m - K)]
Produkt •	wody	powa	zamar­
	m	(ikr)	zania	t > tkr\	t<tkr	t>tkr	t<tkr	t>tkr	t<tkr I
	[%]	[°CI 9	0?z) [kJ/kg]	Po		Co	ce	Ao	A*
Owoce					\
Agrest	88,3	-1,70	293,6		-	3,77	1,93	0,55	1,88
Czarne jagody	82,3	-1,90	275,0	1000	950	3,60	1,89	0,53	1,76
Jabłka	84,1	-2,00	282,0	990	-	3,60	1,89	0,54	1,79
Maliny	82,0	-1,05	283,8	998	-	3,56	1,88	0,53	1,82
Porzeczki czerwone	84,7	-1,00	279,6	1000	950	3,69	1,89	0,53	1,86
Porzeczki czarne	84,7	-1,00	279,6	1000	950	3,69	1,89	0,53	1,86
Śliwki	85,7	-2,20	286,1	1030	980	3,68	1,88	0,54	1,80
Truskawki	90,0	-1,15	289,6	950	840	3,88	2,01	0,56	1,95
Wiśnie	83,0	-3,30	279,6	1040	990	3,64	1,89	0,53	1,67
Warzywa
Brukselka	84,9	-0,55	284,3	-	-	3,69	1,92	0,54	1,91
Buraki	87,6	-0,50	293,6	1053	-	3,77	1,92	0,55	1,96
Fasola szparagowa	88,9	-1,30	298,2	950	890	3,81	1,97	0,55	1,92
Groszek zielony	74,3	-1,10	247,0	1020	-	3,31	1,76	0,50	1,66
Marchew	88,2	-1,35	293,6	1035		3,77	1,92	0,57	1,90
Pomidory	94,1	-0,85	312,2	1000	940	3,98	2,01	0,57	2,06
Szpinak	92,7	-0,95	307,6	-	-	3,94	2,01	0,57	2,02
Ziemniaki	77,8	-1,70	258,6	1055	-	3,44	1,80	0,52	1,69
Mięso
Wieprzowina tłusta	39,0	-2,20	130,7	950	900	2,60	1,87	0,39	0,96
Wieprzowina chuda	60,0	-2,20	201,0	1000	-	2,85	1,34	0,44	1,56
Wołowina tłusta	51,0	-2,20	172,0	950	- •	2,55	1,49	0,43	1,18
Wołowina chuda	72,0	-2,00	241,3	980	-	3,25	1,76	0,52	1,57
Drób
Kurczęta	74,0	-2,50	246,6	- •	. - '	3,31	1,87	0,41	1,57
Indyki	74,0	-2,50	246,6		-	3,31	1,87	0,50	1,62
Ryby
Dorsz	80,0	-2,20	259,8	1000	-	3,77	2,05	0,54	1,70-
Śledź	70,0	-2,20	230,5 •	-	k	3,18	1,72	0,49	1,5
Nabiał
Mleko	! 87,5	-0,60	288,4	1000	-	3,89	2,05	0,53	1,95
Masa jajowa	67,0	-2,80	232,6	-	-	3,18	1,68	0,48	1,42
JLody	[ 60-65		217,7	-	-	3,27	1,88	0,49	-

-brakdanych. O —- £jp * O

~ JO I ^

D / i I

Tabela f Zestawienie współczynników wnikania ciepła (a) w różnych metodach mrożenia

Metoda zamrażania	Współczynnik a
	[W/(m^2 • K)]
Komora gęsto załadowana, znikoma wentylacja	3-4
Tunele owiewowe przy słabej wentylacji; u= 1-3 m/s	8-15
I Tunele owiewowe z silną wentylacją; u = 3-6 m/s, aparaty
1 owiewowe specjalne z ukierunkowanym strumieniem
powietrza (automatyczne zamrażalnie stelażowe, aparaty
spiralne)	20-40
Zamrażanie fluidyzacyjne	130-180
Aparaty kontaktowe	500-1000
Zamrażanie immersyjne, ruch roztworu:
■ słaby	300-400
■ silny	500-700
Aparat LIN (natrysk ciekłego azotu)	1000-2000

temperatura medium chłodzącego

czas

Rysunek 8.3. Wyznaczanie wartości temperatury: t_s, t_w, t_c, t_mp, t_m!c (objaśnienia w tekście)

Całkując równanie (8.4) w ptzedziale X (0, x_z) i jc (0, IJ2), uzyskuje się czas właściwego zamrażania płyty o grubości l_e:

-2 A

l /" _ ^e

a 4X,

q_zpz 2At

(8.6)

T =

V

W analogiczny sposób wyprowadza się wzory do obliczania czasu zamraża­nia materiałów o innych kształtach:

dla walca o średnicy d_e oziębianego na powierzchni bocznej

41 \

d_e d_c

a 4\ v /

IzPz

4At

5.7)

X₇ =

dla kuli o średnicy d_e.

J2\

a Kkg

Z analizy wzorów (8.6), (8.7) i (8.8) wynika, że walec zamarza w tych samych warunkach dwa razy szybciej, a kula trzy razy szybciej niż płyta o grubości l = d, czyli:

kuli • Iz walca • ^z płyty ~ 1 • 2 . 3

Dla prostopadłościanu o wymiarach a, b, l, przy czym a>b>l, oziębianego ze wszystkich stron, otrzymuje się równanie:

q_z p_z ( l_e li

_x p-^ + R^- i (8.9)

^z At a X_e ^{v y}

V 1

gdzie współczynniki P i R zależą od stosunku boków a :l\b:l. Wartości tych współczynników podano w tabeli 8.3.

(8.10)

W dotychczasowych rozważaniach przyjmowano, że temperatura początko­wa zamrażanego produktu była równa jego temperaturze krioskopowej. W rze­czywistości temperatura początkowa produktu jest znacznie wyższa, a tempera­tura końcowa znacznie niższa od temperatury zamarzania. Stąd całkowity czas zamrażania można ująć wzorem:

x = x₀ + x_z + %ęi

gdzie: x₀ - czas schładzania od temperatury początkowej (t_p) do krioskopo- wej {tfa) [s]; Xj - czas domrażania produktu do założonej temperatury końcowej

<lzPz

6A t

Oe) [S].

(8.11)

Przyjmuje się, że czas wstępnego schładzania przedłuża czas zamrażania o 10-20%, czas domrażania zaś o 10-18%. W sumie dla przybliżonych obliczeń przyjmuje się, że:

x = (1,2 do 1,4) x_z

W przedstawionej metodzie obliczania czasu zamrażania z podziałem na trzy etapy, tj. wstępnego schładzania, właściwego zamrażania i domrażania, założono całkowicie umowne rozdzielenie etapów procesu. Praktycznie wszystkie te etapy

mem UL li sności współczynników P i R do obliczenia czasu zamrażania prostopadłościanu ozię- asaesrsE-siszystkich stron (według Pianka: Handbuch der Kaltetechnik Bd. X. Springer Yerlag, 1960)

Stosunek boków		Wymiary stosowane w		praktyce	Współczynniki
a/l	b/l	a	b	l	^7 P	R
1,0	1,0	-	-	-	0,1677	0,0417
1,5	1,0	75	50	50	0,1875	0,0491
	1,5	-	-	-	0,2143	0,0604
	1,0	_	i _	i	0,2000	0,0525
		100	75	50	-	-
2,0	1,5	200	150	100	0,2308	0,0656
		400	300	200	-	-
	2,0	-	-	-	0,2500	0,0719
	1,0	-	_	_	0,2083	0,0545
2,5	2,0	100	80	40	0,2632	0,0751
	2,5	-	-	- ,	0,2778	0,0792
	1,0	—	—	—	0,2142	0,0558
	2,0	150	100	50	0,2727	0j0776
		300	200	100	-	-
3,0	2,25	100	75	33	0,2812	0,0799
		200	150	66	-	-
	3,0	-	OOl^i*'		0,3000	0,0849
3,5	1,0	_	_		0,2186	0,0567
	3,5		-		0,3181	0,0893
	1,0		_	_	0,2222	0,0574
4,0	3,0	200	150	50	0,3156	0,0887
	4,0	-	-	-	0,3333	0,0929
	1,0	-	—	—	0,2250	0,0580
4,5	3,0	150	100	33	-	-
		300	200	66	0,3215	0,0902
	4,5	-	-	-	0,3460	0,0959
	1,0	200	150	33	0,2308	0,0592
6,0	4,5	400	300	66	0,3602,.	0,0990
	6,0	-	-	-	0,3750	0,1020

przebiegają jednocześnie i rozgraniczenie ich jest niemożliwe. Do przybliżonego obliczania całkowitego czasu zamrażania zaleca się stosowanie wzoni uproszczo­nego, operującego wyłącznie wartościami entalpii początkowej i końcowej, które mogą być ściśle określone.

(8.12)

Według tej zasady całkowity czas zamrażania wyraża się wzorem ogólnym:

₌ a_lPz(u 2BAt la 4Xe

gdzie: Ai= i_p — i_e — różnica entalpii produktu w temperaturze początkowej(/p) i końcowej (t_e) [kJ/kg]; B - współczynnik zależny od kształtu ciała, który dla płyty wynosi 1, dla walca 2, a dla kuli 3. & ^{1 C}

Z czasem zamrażania ściśle wiąże siępojęcie szybkości zamrażania. Określa oria szybkość, z jaką front formacji lodowej przesuwa się w głąb ciała zamraża­nego. Szybkość ta nie jest wartością stałą, lecz zmienia się wraz z odległością od powierzchni zewnętrznej ciała oziębianego; wyraża się więc ona równaniem różniczkowym:

^{w =} f <⁸¹³>

Zmniejszenie się szybkości zamrażania związane jest ze wzrostem oporu przewodzenia ciepła w miarę przesuwania się frontu lodowego w głąb zamraża­nego materiału.

Zazwyczaj operuje siępojęciemtzw. średnią liniowej szybkości zamrażania, którą otrzymuje się, dzieląc grubość zamrażanej warstwy przez czas zamrażania:

w = — * V ■ f (8.14)

^Xz /

gdzie 8 - odległość od tzw. termicznego środka produktu do oziębianej po- t wierzchni.

Termiczny środek produktu jest to punkt o najmniejszej szybkości zamraża­nia, czyli punkt najpóźniej zamarzający. Dla ciał jednorodnych punktten pokrywa ^ się ze środkiem geometrycznym i wówczas zamiast 5 należy wstawiać dla walca o nieskończonej długości i kuli dl2, a dla płyty meśkóńbzonej //2.

Ponadto w praktyce zamrażalniczej operuje się pojęciem efektywnej szyb­kości zamrażania jako wynikiem - podzielenia połowy grubości produktu (mie- [rzonej przez jego środek termiczny) przez efektywny czas zamrażania:

w = — (8.15)

Efektywny czas zamrażania to czas konieczny do obniżenia temperatury produktu o danym kształcie od jednolitej średniej temperatury początkowej (t_p)do określonej przez technologię temperatury efektywnej (t_e) w jego środkuj termicznym. Często efektywny czas zamrażania utożsamiany jest z całkowitym i czasem zamrażania.

Wielkości 8, dii podaje się zwykle w cm, t_z i x_e zaś w h; zatem wielkości! w i w_e są określone w cm/h.

Wpływ różnych czynników na proces zamrażania

Wymiary i kształt ciała

Na czas zamrażania wpływa głównie grubość zamrażanego ciała. Inne wymiary są mniej ważne. Przy większych grubościach wpływ ten staje się dominujący, gdyż rośnie proporcjonalnie do / lub S.

Równie istotny jest kształt ciała. Przy tych samych grubościach najkorzyst­niejszy jest kształt kuli, potem walca i prostopadłościanu oziębianego ze wszy­stkich stron. Najmniej korzystna jest postać płyty.

Różnica temperatury

Jak wynika ze wzorów: (8.6), (8.7), (8.8) i (8.9), czas zamrażania jest odwrot­nie proporcjonalny do różnicy temperatury między zamrażanym produktem i czyn­nikiem chłodzącym. Różnica temperatury odgrywa dużą rolę, gdy współczynniki wnikania ciepła są małe (zamrażarki owiewowe). Wtedy skrócenie czasu zamra­żania jest możliwe głównie przez obniżenie temperatury powietrza.

Współczynnik przenikania ciepła

Jego wartość uzależniona jest od oporów cieplnych wnikania i przewodzenia. Opór cieplny wnikania przeważa nad oporem cieplnym przewodzenia przy za­mrażaniu surowców o małej grubości. Przy większych grubościach zamrażanego produktu większą rolę odgrywa opór cieplny przewodzenia.

Orientacyjne wartości współczynnika wnikania ciepła (a) wahają się w sze­rokich granicach, zależnie od typu zamrażarki i metody mrożenia (tab. 8.2).

Dla produktów najczęściej zamrażanych w tunelach i aparatach owiewowych (tusze, ćwierci, kartony, skrzynki) opracowano liczne wzory empiryczne pozwa­lające obliczyć współczynnik a. Jednym z nichjest równanie Grudy i Postolskiego:

a = 9,7 u⁰'⁶⁹ (8.16)

gdziejw - prędkość strumienia powietrza w wolnym przekroju tunelu [m/s].

Opakowanie

Opakowanie utrudnia warunki przepływu ciepła od powierzchni produktu do medium chłodzącego. Stąd wzór na czas właściwego zamrażania płyty przyjmuj e następującą postać:

gdzie op - sumaryczny opór cieplny opakowania [(m² • K)/W].

W podobny sposób należy skorygować wzory dla walca, kuli i prostopadło­ścianu: (8.7), (8.8), (8.9) oraz wzory uproszczone (8.12).

Opakowanie, zwłaszcza wielowarstwowe, znacznie wydłuża czas zamraża­nia, przy czym największy opór cieplny wynika nie z grubości opakowania i jego przewodności cieplnej właściwej, lecz z warstewki powietrza zawartej między produktem a opakowaniem lub między jego poszczególnymi warstwami. Opór ten można zredukować za pomocą odpowiedniego docisku lub stosowania pako­wania pod zredukowanym ciśnieniem i folii termokurczliwych. W tabeli 8.4 zestawiono wartości oporu cieplnego różnego typu opakowań.

Tabela 8.4. Opór cieplny opakowań produktów mrożonych przy nacisku p—l kPa (według Bergelunda, Jonssona, Szeffira i Watzingere) ^ .. ^c

Opakowanie	Gramatura	Grubość	Opór cieplny
	[g/m^2]	[mm]	[m^2 • K/W]
Pergamin	64		0,00142
Półpergamin parafinowany	60		0,00359
Karton parafinowany - półpergamin	48-60		0,00506
Karton parafinowany		0j625	0,00826
Celofan lub polietylen		0,028	0,00028
Celofan czterowarstwowy		4 x 0,028	0,00112
Folia celofanowa		0,146	0,00224
Pergamin podwójnie woskowany		0,212	0,0030
Karton wyłożony folią aluminiową		0,568	>0,0069,
Karton z woreczkiem celofanowym wewnętrznym			0,0162
Karton parafinowany owinięty w celofan cztero­
warstwowy		0,757	0,0094
Folia aluminiowa		0,4	0,0000005
Papier woskowany		-	0,0052
Papier woskowany + karton		-	0,0155
Warstewka powietrza		0,7-0,9	0,404
Forma z blachy aluminiowej		2,0	0,0000098
Forma z blachy stalowej kwasoodpornej		1,0	0,000066
Folia PCV		0,25	0,0025
Folia PE		0,004	0,000138
Tektura falista		4,0	0,022
Papier do pakowania		0,1	0,00143

Bilans ciepła procesu zamrażania

Dość ciepła, którą trzeba odebrać od zamrażanego produktu, określa się równaniem:

QfM(q_l + q₂+q₃+q₄+q₅) (8.18)1

gdzie M- masa produktu [kg].

Natomiast poszczególne pozycje bilansu ciepła mogą być obliczone z nastę­pujących wzorów:

qi = c₀(t_p-th) (8.19)

gdzie: q\ - ciepło schładzania produktu od temperatury początkowej do kriosko- powej JJkJ/kg]; c₀ - ciepło właściwe produktu nie zamrożonego [kJ/(kg • K)];

q₂= , (8.20)

gdzie: qi - ciepło przemiany fazowej wody w lód [kJ/kg]; W- zawartość wody w produkcie [kg/kg]; © - udział wody wymrożonej w produkcie [kg/kg]; q_zw - utajone ciepło zamarzania wody [kJ/kg];

q₃=W(Qc_L(t_kr-t_e) (8.21)

gdzie: <73 - ciepło obniżania temperatury lodu do temperatury końcowej [kJ/kg]; c_L - ciepło właściwe lodu, 2,1 kJ/(kg • K);

q_Ą = {l-m)Wc_p{t_kr-t_e) (8.22)

gdzie: <74 - ciepło obniżania temperatury nie zamrożonej fazy ciekłej do tempe­ratury końcowej [kJ/kg]; c_p - ciepło właściwe nie wymrożonej fazy płynnej [kJ/(kg • K)], dla większości produktów spożywczych przyjmuje się wartość 3,77 kJ/(kg • K); *

q₅ = {l-W)c_s{t_kr-Q (8.23)

gdzie: q₅ - ciepło obniżania temperatury suchej substancji do temperatury koń­cowej [kJ/kg]; c_s - ciepło właściwe suchej substancji [kJ/(kg • K)], dla większości produktów spożywczych przyjmuje się wartość 1,21 kJ/(kg • K).

Ponadto w obliczeniach technicznych można stosować uproszczoną metodę, uwzględniającą różnicę entalpii zamrażanego produktu:

Q = M Ai (hi : (8-24)

Cel ćwiczenia

Celem ćwiczenia jest wykreślenie krzywych mrożenia wybranego produktu spożywczego, przeanalizowanie rozkładu wartości temperatury w zamrażanej próbce przy przewodzeniu ciepła przez ściankę płaską (płyta, sześcian), przez ściankę cylindryczną (walec) lub przez ściankę kulistą, porównanie praktycznego i teoretycznego czasu , zamrażania oraz obliczenie bilansu cieplnego procesu zamrażania. C/^ - Lu., -- ^ ^cf(

Opis stanowiska pomiarowego

Stanowisko doświadczalne do badań składa się z zestawu urządzeń i aparatów przedstawionych na rysunku 8.4.

Rysunek 8.4. Stanowisko doświadczalne do zamrażania badanych próbek: 1 - zamrażalnik, 2 - sprężarka, 3-skraplacz, 4-rurka kapilarna, 5-wentylator, 6 - termometr alkoholowy, 7-pokrywa z wmontowanymi termoparami, 8 - rejestrator, 9 - termopary, 10 - badana próbka

fBzwtstawionym zestawie można wyodrębnić dwa układy:

1. Układ chłodzący, składający się z chłodziarki sprężarkowej (czynnik' chłodniczy - freon 12) z rozbudowaną komorą zamrażania, wewnątrz której znajduje się wentylator w celu wyrównania temperatury medium chłodzącego (powietrza) i zwiększenia współczynnika wnikania ciepła.

2. Układ do pomiaru temperatury, zbudowany z siedmiu termoelementów miedź-konstantan. Spoina odniesienia jest umieszczona w mieszaninie wody z lodem o temperaturze 0°C. Termoelementy są podłączone do dwóch miliwol- tomierzy (trzy termoelementy - do pierwszego i cztery termoelementy - do drugiego), mierzących zmiany siły termoelektrytcznej w czasie. Czwarty termo- element jest podłączony do drugiego miliwoltomierza i mierzy on wartość siły termoelektrycznej odpowiadającej temperaturze powietrza w komorze.

Wykonanie ćwiczenia

Przygotowanie materiału

Wykroić z surowców (marchew, ziemniak, burak, jabłko) kostkę o boku 25 (30) mm, walec o średnicy 25 (30) mm i wysokości h (objętość kostki powinna być równa objętości walca) lub kulę o średnicy 25 (30) mm. Wprowadzić do kostki

• walca lub walca i kuli po 3 termoelementy, umieszczając je: w środku termicz­nym próbki, w połowie odległości od środka termicznego i na powierzchni próbki.

Metodyka pomiarów

Włączyć obieg czynnika chłodniczego i wentylator.

Włączyć zasilanie miliwoltomierzy i przeprowadzić zerowanie wskazań.

Odczytać na miliwoltomierzach w czasie zerowym, przed wprowadzeniem próbek do komory zamrażalnika, wartości siły termoelektrycznej odpowiadającej temperaturze trzech warstw próbki w otoczeniu.

Wprowadzić materiał badany do komory zamrażarki w momencie, gdy termoelementy wykażą jednakową temperaturę w całej próbce.

Odczytać na miliwoltomierzach wartości zmian siły termoelektrycznej w czasie. Pierwsze odczyty wykonywać co 30 sekund przez 5 minut, następne co

• minuty do momentu uzyskania w środku termicznym próbki temperatury -5°C. Dalsze pomiary wykonywać co 1 minutę.

Uwaga. W chwili gdy świecąca plamka na skali miliwoltomierza dojdzie do pozycji 0 mV, zmienić bieguny za pomocą przełączników i odczytać ujemną wartość siły termoelektrycznej (temperatura minusowa).

Zakończyć proces zamrażania w momenciehgdy temperatura w środku termicznym próbki osiągnie wartość około -15°C.

Wyłączyć obieg czynnika chłodniczego, wentylator, miliwoltomierze i wyjąć zamrożone próbki z komory zamrażarki.

Opracowanie i interpretacja wyników

1. Przeliczyć wartości siły termoelektrycznej na temperaturę na podstawie równania krzywej wzorcowej podanego przez prowadzącego ćwiczenia.

2. Wykreślić krzywe mrożenia wybranego produktu spożywczego dla po­szczególnych punktów pomiarowych. Ponadto na tym samym wykresie przed­stawić krzywą zmian temperatury powietrza w komorże zamrażarki.

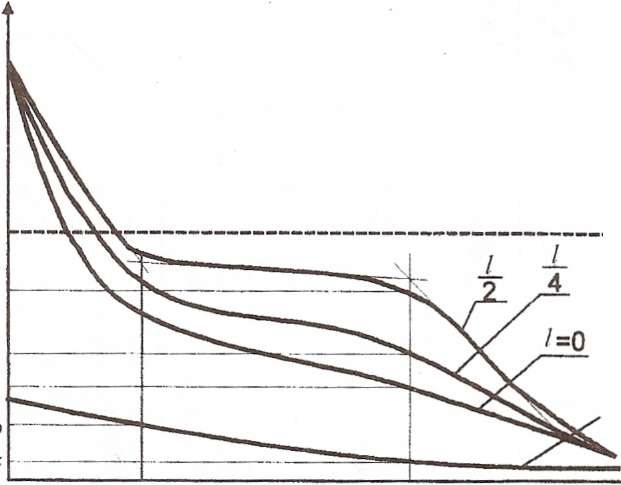
3. Przeanalizować rozkład war­tości temperatury w zamrażanej prób- pe w charakterystycznych etapach procesu zamrażania. Na podstawie krzywych mrożenia wykonać wykres, odkładając na osi rzędnych odczytaną temperaturę w °C, a na osi odciętych - odległość od powierzchni próbki w danym czasie. Przykładowy wy-J kres przedstawiono na rysunku 8.5.

4. Porównać praktyczny i teore­tyczny czas zamrażania. Praktyczny czas zamrażania (ip) wyznaczyć na podstawie krzywej mrożenia przed- 5 , „ „ „ ,, ,

^{r J} ■> ^r Rysunek 8.5. Rozkład wartości temperatury w za­

stawiaj ącej zmiany temperatury _mrażanej~pYób(x

w centrum termicznym próbki.

5. Wykorzystując bilans cieplny procesu zamrażania, obliczyć ilość ciepła, jaką należy odprowadzić od 1 kg zamrażanego produktu spożywczego.

6. Sformułować wnioski.

— 76'

— 75 —

— 74 —

— 80

— 79

— 77 —

— 84 —

—83 —

81

— 88 —

-—85 —

— 92 —

— 85 —

---