Laboratorium metrologii elektrycznej i elektronicznej . |
|
|
ĆW.NR 10 |
WOJCIECH KRZESAJ MIROSłAW JENŚ |
GR.3 |
DATA: 98-02-27. |
Temat: Badanie galwanometru statycznego . |
OCENA: |
1. CEL ĆWICZENIA
Celem ćwiczenia było poznanie budowy i zastosowanie galwanometru statycznego oraz wyznaczenie jego podstawowych parametrów.
2. SCHEMATY POMIAROWE
2.1. Schemat układu do badania galwanometru
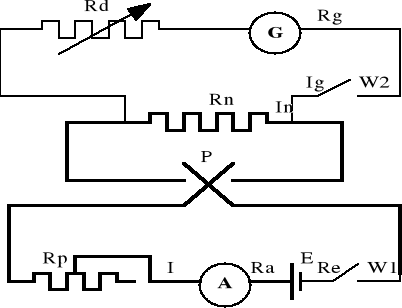
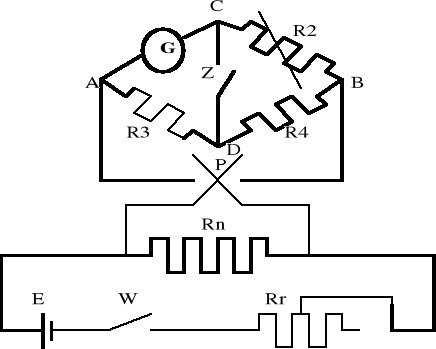
2.2. Układ połączeń do pomiaru rezystancji galwanometru metodą
przesuniętego zera.
3. POMIARY-OBLICZENIA-BŁĘDY
3.1. Pomiar okresu drgań galwanometru nietłumionego To
(Wyznaczenie błędu pomiaru )
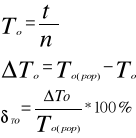
t |
n |
To |
Topop |
ΔTo |
δTo |
[s] |
[-] |
[s] |
[s] |
[s] |
[%] |
13 |
10 |
1.3 |
1.4 |
0.1 |
7.14 |
3.2.Wyznaczanie rezystancji krytycznej Rk
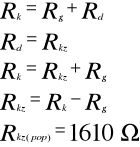
Błędy wyniku pomiaru
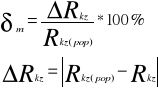
Rd=Rkz |
Rp |
Rk |
Rg |
t |
m |
Rkz |
pk |
[ ] |
[ ] |
[ ] |
[ ] |
[ s ] |
[ % ] |
[ ] |
[ % ] |
1600 |
900 |
1790 |
190 |
2,5 |
0,6 |
10 |
0,05 |
1650 |
860 |
1840 |
190 |
2,0 |
2,2 |
40 |
0,05 |
1750 |
800 |
1940 |
190 |
3,0 |
8,7 |
140 |
0,05 |
3.3. Pomiar czasu ustalenia się galwanometru dla przebiegu krytycznego
Po nastawieniu rezystancji krytycznej zewnętrznej galwanometru równej rezystancji krytycznej Rkz = 1650 czas do chwili ustalenia się galwanometru dla przebiegu krytycznego wynosi t = 2 [s].
3.4. Pomiar rezystancji galwanometru metodą dwóch odchyleń.
Tabela pomiarowa
Rd |
a |
a1 |
a2 |
Rn |
I |
[ ] |
[mm] |
[mm] |
[mm] |
[ ] |
[mA] |
2200 |
99,5 |
99 |
100 |
1 |
2,4 |
1360 |
160,5 |
159 |
162 |
1 |
2,4 |
1100 |
195,5 |
199 |
192 |
1 |
2,4 |
Obliczenia
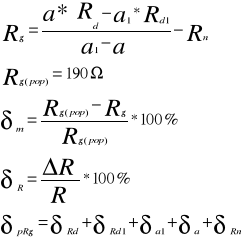
Tabela z wynikami obliczeń
a |
a1 |
Rd |
Rd1 |
Rg |
m |
pRg |
[mm] |
[mm] |
[ ] |
[ ] |
[ ] |
[%] |
[%] |
99,5 |
160,5 |
2200 |
1360 |
10 |
94,7 |
1,72 |
160,5 |
195,5 |
1360 |
1100 |
92 |
51,5 |
1,23 |
99,5 |
195,5 |
2200 |
1100 |
40 |
78,9 |
1,61 |
3.5. Pomiar Rg metodą przesuniętego zera
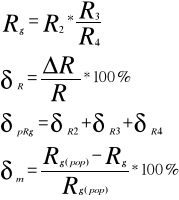
Tabela pomiarów i obliczeń
R2 |
R3 |
R4 |
Rr |
Rg |
Rg(pop) |
m |
pRg |
[ ] |
[ ] |
[ ] |
[ ] |
[ ] |
[ ] |
[%] |
[%] |
2100 |
500 |
5000 |
900 |
210 |
190 |
10,5 |
0,15 |
3.6. Wyznaczenie stałej prądowej Ci i stałej napięciowej C 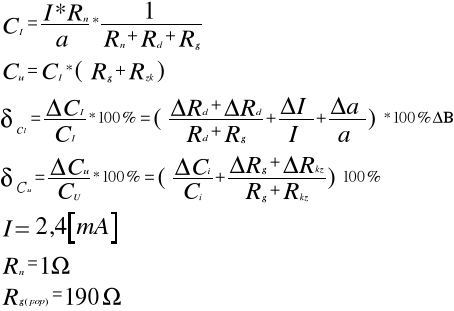
Tabela wielkości podstawianych do wzoru
|
|
|
|
a |
Rd |
Rg(pop |
Rg |
[mm] |
[ ] |
[ ] |
[ ] |
99,5 |
2200 |
190 |
10 |
160,5 |
1360 |
190 |
92 |
195,5 |
1100 |
190 |
40 |
Tabela wyników obliczeń
Ci (Rgpop) |
ci |
Ci (Rg) |
ci |
Cu |
cu |
A/dz |
[%] |
[A/dz] |
[%] |
[V/dz] |
[%] |
9,8*10^-9 |
2,10 |
10,8*10^-9 |
2,15 |
2,6*10^-5 |
2,2 |
9,6*10^-9 |
0,80 |
10,2*10^-9 |
0,85 |
1,6*10^-5 |
0,9 |
9,2*10^-9 |
1,22 |
5,3*10^-9 |
1,27 |
0,6*10^-5 |
1,3 |
4.UWAGI I WNIOSKI
Galwanometrem nazywamy elektryczny przyrząd pomiarowy o bardzo dużej czułości. Ze względu na budowę ustroju można je podzielić na magnetoelektryczne, elektrodynamiczne itd. Oprócz tego można jeszcze dzielić galwanometry na przenośne i nieprzenośne. W ćwiczeniu badaliśmy galwanometr nieprzenośny , w takim galwanometrze ustawia się skalę w większej odległości od organu ruchomego -żródła światła ( zwykle 1000 mm.), powoduje to że zwiększa się czułość przyrządu.
Wyznaczając okres drgań galwanometru nietłumionego To należy zwrócić uwagę na fakt że przebieg nietłumiony jest praktycznie niemożliwy i otrzymany błąd wyniku pomiaru ma tu swoje uzasadnienie.
Rezystancja krytyczna galwanometru Rk, to rezystancja całego obwodu galwanometru, przy której występuje ruch krytyczny. Składa się ona z rezystancji wewnętrznej Rg i rezystancji zewnętrznej Rkz. Rezystancja zewnętrzna krytyczna to rezystancja przyłączona do galwanometru przy której następuje ruch krytyczny. Przy rezystancji krytycznej Rk = 1840[] uzyskaliśmy najkrótszy czas ustalenia się galwanometru dla ruchu krytycznego t = 2 [s].
Pomiar rezystancji galwanometru metodą 2-odchyleń karze nam wnioskować że małe wychylenie wskazówki galwanometru i mała różnica pomiędzy dwoma wychyleniami daje większą dokładność wyznaczenia oporu Rg. Zaś przy wychyleniu większym i różnicy dużej dokładność wyznaczonego oporu Rg maleje i powstaje duży błąd. Ogólnie podsumowując stwierdzamy że metoda ta naszym zdaniem nie nadaje się do pomiaru rezystancji galwanometru Rg.
Dokładniejszą metodą wyznaczania rezystancji Rg potwierdzoną teoretycznie i przez nas za najdokładniejszą jest metoda przesuniętego zera podana przez Thomsona (mały błąd ).
Na podstawie ściągniętych pomiarów i obliczeń wyznaczyliśmy stałą prądową Ci i stałą napięciową Cu jak widać z obliczeń stała prądowa otrzymana przez nas z obliczeń różni się od stałej odczytanej z badanego galwanometru Ci =3,5*10^-9 A/dz.
6
Wyszukiwarka
Podobne podstrony:
Badanie galwanometru statycznego v8
Badanie galwanometru statycznego v10
Badanie galwanometru statycznego, AGH IMIR Mechanika i budowa maszyn, II ROK, Metrologia Tyka Haduch
Badanie galwanometru statycznego, I. Cel ˙wiczenia.
Badanie galwanometru statycznego4
Badanie galwanometru statycznego v7
Badanie galwanometru statycznego v9
Badanie galwanometru statycznego v2
Miernictwo- BADANIE GALWANOMETRU STATYCZNEGO, II ElektrycznyGrupa ?wiczeniowa 5_
Badanie galwanometru
Badanie galwanometru statycznego5
Badanie zjawisk galwanomagnetycznych, Badanie zjawisk galwanomagnetycznych
Badanie zjawisk galwanomagnetycznych, Badanie zjawisk galwanomagnetycznych
37 Badanie drgań tłumionych cewki galwanometru zwierciadłowego
Badanie ruchu ramki galwanometru2, Szkoła, penek, Przedmioty, Fizyka, Laborki
Badanie przekształtnika DC DC obnizającego napięcie w układzie mostkowym z izolacją galwaniczną
Badanie ruchu ramki galwanometru, Szkoła, penek, Przedmioty, Fizyka, Laborki
Badanie ruchu ramki galwanometru ?danie ruchu ramki galwanometru 1
więcej podobnych podstron