Politechnika Warszawska Wydział Elektryczny Zakład Elektrotechniki Teoretycznej |
Laboratorium Elektrotechniki Teoretycznej |
||
Rok Semestr Gr. |
Data godz.
|
Ćwiczenie nr 5 Temat: Badanie stanów nieustalonych w obwodach elektrycznych. |
|
Zespół nr :
|
Prowadzący:
|
Ocena:
9 pkt/10 |
|
Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się z zachowaniem się obwodu szeregowego RC, RL, RLC o parametrach skupionych przy załączaniu i wyłączaniu napięcia stałego, poznanie metod analizy i obserwacji stanów nieustalonych.
Wprowadzenie teoretyczne:
Załóżmy, że do gałęzi szeregowej R, L, C przyłożono napięcie stałe E. W chwili t=0 prąd w obwodzie nie płynie i(0)=0. Nie występuje także napięcie na zaciskach kondensatora uc(0)=0. Z chwilą przyłożenia napiecia E do obwodu kondensator zaczyna się ładować. Przebiegi napięc na elementach R, L i C są opisane wg. zależności różniczkowych (cewka) jak również zależności całkowe (kondensator). Oto one:
![]()
Po załączeniu napięcia E do układu w rozpatrywanym obwodzie nastąpi ładowanie kondensatora prądem płynącym również przez cewkę.
Rozwiązując równanie powyżej można wyliczyć przebiegi napięć i prądów w obwodzie w stanie nieustalonym. Rozróżnia się trzy przypadki:
Przypadek
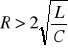
, rezystancja gałęzi jest wększa od rezystancji krytycznej (aperiodyczny). Zależności przedstawiają się następująco:
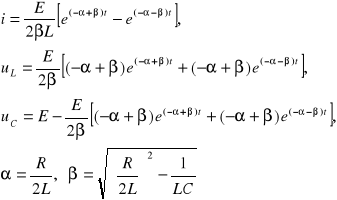
2. Przypadek: ![]()
, rezystancja gałęzi jest równa rezystancji krytycznej. To jest tak zwany przypadek aperiodyczno-krytyczny. Zależności przedstawiają się następująco:
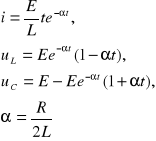
Przypadek:
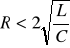
, rezystancja gałęzi jest mniejsza od rezystancji krytycznej. To jest tak zwany przypadek oscylacyjny. Zależności przedstawiają się następująco:
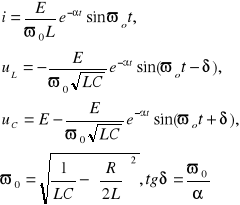
W ćwiczeniu badaliśmy również przypadki szczególne. Obwód składający się z dwóch elementów RL lub RC. W obu przypadkach mamy do czynienia z przebiegami aperiodycznymi. Zależności ogólne upraszczają się wówczas do postaci:
* przypadek RL
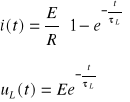
* przypadek RC
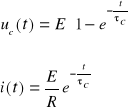
gdzie ![]()
jest stała czasową obwodu RC, a ![]()
jest stałą czasową obwodu RL
Obserwacje na oscyloskopie prądów, napięć i trajektori fazowych w gałęzi RLC:
Przypadek aperiodyczny:
R=2000 [Ω]
L=1,06 [H]
C=2 [µF]
Przypadek oscylacyjny:
R=200 [Ω]
L=1,06 [H]
C=2 [µF]
Przypadek aperiodyczny krytyczny:
R=1200 [Ω]
L=1,06 [H]
C=2 [µF]
Obliczenia:
Obliczenia dla napięcia stałego E w obwodzie RLC.
Przypadek aperiodyczny.
R=2000 [Ω], L=1,06 [H], C=2 [µF]
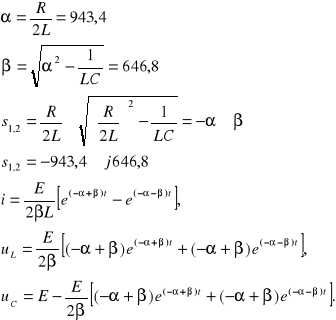
Przypadek oscylacyjny.
R=200 [Ω], L=1,06 [H], C=2 [µF]
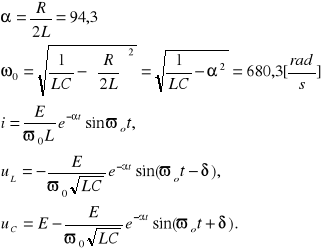
Przypadek aperiodyczny krytyczny.
R=1200 [Ω], L=1,06 [H], C=2 [µF]
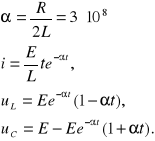
5. Wnioski:
W ćwiczeniu zbadaliśmy stany nieustalone w obwodzie szeregowym RL,RC,RLC.
Charakterystyki prądu i napięć w obwodach szeregowych RL, RC oraz RLC potwierdzają
zależności różniczkowe pomiędzy tymi wielkościami. I tak w obwodzie RL gdy prąd zbliża
się do wartości maksymalnej (funkcja ma ekstremum) to napięcie na cewce zbliża się do zera
(pochodna jest zero). Analogicznie w obwodzie RC gdy napięcie na kondensatorze zbliża się
do wartości maksymalnej (funkcja ma ekstremum) prąd maleje do zera (pochodna jest zero).
Tutaj mogą wystąpić różne sytuacje. Gdy rezystancja ![]()
to mówimy o przypadku aperiodycznym. W takim układzie zmienną stanu jest napięcie na kondensatorze. Z wykresu funkcji napięcia na kondensatorze można wyznaczyć przebieg prądu ![]()
. Można tutaj
zauważyć iż w punkcie największego nachylenia stycznej przebiegu napięcia do osi czasu
występuje maksimum funkcji prądu - zgodnie z prawami pochodnych. Z funkcji prądu można natomiast wyznaczyć przebieg napięcia na cewce ![]()
. Można tutaj zauważyć iż przebieg napięcia nie jest funkcją ciągłą- przy włączeniu wyłącznika napięcie skokowo zmienia się.
W obwodzie RLC dla przypadku aperiodycznego w punkcie przegięcia wykresu napięcia na kondensatorze (tangens kąta nachylenia stycznej do krzywej jest największy) prąd ma wartość maksymalną (pochodna ma wartość maksymalną - tangens kąta nachylenia stycznej do krzywej), natomiast napięcie na cewce ma wartość zero (pochodna prądu). Idąc dalej gdy prąd ma punkt przegięcia (tangens kąta nachylenia stycznej ma wartość ujemną) napięcie na cewce ma wartość ujemną maksymalną. Gdy wartość napięcia na cewce zbliża się do wartości maksymalnej prąd maleje do zera.
W przypadku gdy rezystancja ![]()
mówimy o przypadku oscylacyjnym. Tutaj również zmienną stanu jest napięcie na kondensatorze. Przebieg napięcia na kondensatorze jest funkcją ciągłą . Przebieg tej funkcji ma charakter oscylacyjny- napięcie oscyluje bowiem w pobliżu napięcia zasilania E. Po pewnym czasie przebieg ten (sinusoida) wygasa i dalej mamy do czynienia ze stanem ustalonym - napięcie na kondensatorze jest równe napięciu zasilania obwodu E. Tak samo jak poprzednio prąd „i” jest pochodną napięcia na kondensatorze a napięcie na cewce jest pochodną prądu „i” .Częstotliwość własna w takim przypadku mówi nam o częstotliwości gasnącej sinusoidy. Natomiast stała tłumienia mówi nam jak szybko przebieg sinusoidalny będzie wygaszany - wygaszanie to zachodzi zgodnie z funkcją wykładniczą. Im większa stała tłumienia tym stan nieustalony będzie trwał krócej.
W obwodzie RLC dla przypadku oscylacyjnego przebiegi w pierwszej fazie są takie same jak dla przypadku aperiodycznego, aż do momentu gdy napięcie na kondensatorze osiągnie wartość maksymalną. Po tym czasie przebiegi są sinusoidalne tłumione, napięcie na kondensatorze oscyluje wokół wartości E, natomiast prąd i napięcie na cewce oscylują wokół zera. Zgodnie z zależnościami różniczkowymi gdy napięcie na kondensatorze ma ekstrema, to prąd przyjmuje wartości zerowe, natomiast gdy prąd ma ekstrema napięcie na cewce przyjmuje wartości zerowe.
1
1
Wyszukiwarka
Podobne podstrony:
stany nieustalonerc, Politechnika Lubelska
stany nieustalone, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 12. Stany n
stany nieustalone w obwodach RLC zasilanych ze źródła napięcia stałego, Politechnika Lubelska, Studi
GOTOWE, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 12. Stany nieustalone
Stany nieustalone w obwodach z elementami RC, Politechnika Lubelska, Studia, ELEKTROTECHNIKA LABORAT
Stany nieustalone moje, Politechnika Lubelska, Studia, Elektrotechnika, ELEKTROTECHNIKA LABORATORIUM
Stany nieustalone w obw.RC, Politechnika Lubelska w Lublinie
08 Stany nieustalone w obwodach RLCid 7512 ppt
A2-3, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria kom
SPRAWKO STANY NIEUSTALONE, Elektrotechnika, Elektrotechnika
slajdy TIOB W27 B montaz obnizone temperatury, Przodki IL PW Inżynieria Lądowa budownictwo Politechn
stany nieustalone w RC, Elektrotechnika-materiały do szkoły, Elektrotechnika
więcej podobnych podstron