WOJSKOWA AKADEMIA TECHNICZNA
--------------------------------------------------------------------------------------------------------
LABORATORIUM FIZYCZNE
Grupa szkoleniowa C-21 Podgr. 1 płk. Walczak
stopień i nazwisko
prowadzącego
st. szer. pchor. Jarosław FIUT
st. szer. pchor. Dariusz CHMIELEWSKI
(stopień, imię i nazwisko słuchacza)
ocena końcowa ocena przygot.
do ćwiczenia
SPRAWOZDANIE
Z
PRACY LABORATORYJNEJ Nr 28
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
WSTĘP TEORETYCZNY.
Zjawisko rozchodzenia się fal o rozmaitych kształtach powierzchni falowych ( np. fal płaskich czy kulistych ), jak również zjawiska: ugięcia ( dyfrakcji ), odbicia i załamania można opisywać za pomocą zasady Huyghensa, wg której każdy punkt ośrodka, do którego dociera czoło fali staje się samodzielnym źródłem wysyłającym elementarne fale kuliste.
Obwiednia elementarnych fal kulistych stanowi nowe czoło fali kulistej. Podobnie jest w przypadku fali płaskiej, gdzie obwiednia fal elementarnych jest płaszczyzną stanowiącą czoło rozchodzącej się fali płaskiej.
Jeżeli rozchodząca się fala natrafia na jakąkolwiek przeszkodę, to powierzchnia falowa ulega zniekształceniu. Zjawisko to nazywamy dyfrakcją albo ugięciem fali. Zjawisko dyfrakcji łatwo jest zaobserwować w przypadku fal rozchodzących się po powierzchni wody. Zjawisko dyfrakcji w przypadku fal dźwiękowych występuje wówczas, gdy źródło dźwięku jest odgrodzone od obserwatora jakąś przeszkodą, np. stojąc za narożnikiem budynku słyszymy odgłos nadchodzącej osoby dzięki temu, że fale głosowe ulegają ugięciu.
Fale świetlne polegają na rozchodzeniu się zmiennych pól: elektrycznego i sprzężonego z nim nierozdzielnie pola magnetycznego. Ich natężenia opisują: wektor elektryczny ( nazywany również wektorem świetlnym, gdyż wywołuje wrażenie świetlne ) i prostopadły do niego wektor magnetyczny. W zjawisku interferencji światła, polegającym na nakładaniu się fal świetlnych, wektory świetlne dodają się ( doświadczenie Younga ).
Przy superpozycji dwóch drgań równoległych o jednakowych częstotliwościach amplitudy drgań dodają się, gdy fazy są zgodne, a odejmują się, gdy fazy są przeciwne .Gdy fazy będą zgodne w punkcie tym wystąpi maksimum. Fazy fal są zgodne, jeżeli na odcinku zawierać się będzie wielokrotność długości fali, czyli gdy:
Jeżeli fazy fal będą przeciwne, to wystąpi minimum, co nastąpi wówczas, jeżeli odcinek będzie zawierał nieparzystą wielokrotność połówek długości fali, czyli
Na podstawie przeprowadzonych powyżej rozważań można stwierdzić, iż : fale o jednakowych długościach wzmacniają się najsilniej, jeżeli różnica ich dróg optycznych jest równa wielokrotności długości fali, a maksymalnie się osłabiają, jeżeli różnica ich dróg optycznych jest nieparzystą wielokrotnością połówek długości fali.
Siatką dyfrakcyjną nazywamy zbiór dużej liczby jednakowych, równoległych szczelin, między którymi występują równe odstępy.
Siatki dyfrakcyjne dzielimy na transmisyjne i odbiciowe. Siatki transmisyjne można uzyskać poprzez nacinanie wzajemnie równoległych i leżących w równych odstępach rys na szkle. Przerwy między nimi pełnią rolę szczelin. Powyższą metodą można otrzymać od kilku do kilkuset linii na jednym mm. Inną metodą jest metoda holograficzna polegająca na bezsoczewkowym fotografowaniu interferencyjnego obrazu dwóch spójnych monochromatycznych fal płaskich, padających pod pewnym kątem względem siebie na kliszę fotograficzną o bardzo dużej zdolności rozdzielczej. Po wywołaniu jasne prążki interferencyjne ( miejsca przezroczyste na kliszy ) spełniają rolę szczelin. W taki sposób można otrzymać siatki dyfrakcyjne o bardzo dużej gęstości linii, nawet do 4000 linii/mm.
W siatkach odbiciowych rysy nacinane są na wypolerowanej powierzchni metalu, a światło padające na miejsca między rysami jest odbijane, dając taki sam rezultat końcowy jak światło przechodzące przez siatkę transmisyjną .
WYNIKI POMIARÓW:
Barwa |
k |
hp [ cm ] |
hl [ cm ] |
l [ cm ] |
Niebieska |
1 |
6,6 |
6,6 |
80 |
|
|
6,6 |
6,6 |
|
|
|
6,7 |
6,7 |
|
|
|
6,6 |
6,7 |
|
|
|
6,6 |
6,6 |
|
|
2 |
7,3 |
7,3 |
|
|
|
7,3 |
7,2 |
80,5 |
|
|
7,2 |
7,2 |
|
|
|
7,3 |
7,3 |
|
|
|
7,3 |
7,3 |
|
Zielona |
1 |
8 |
7,8 |
|
|
|
7,9 |
7,9 |
|
|
|
7,9 |
8 |
80 |
|
|
8 |
8 |
|
|
|
8 |
7,9 |
|
|
2 |
8,2 |
8,2 |
|
|
|
8,2 |
8,2 |
|
|
|
8,2 |
8,2 |
|
|
|
8,1 |
8,2 |
79,5 |
|
|
8,1 |
8,2 |
|
Czerwona |
1 |
9,5 |
9,4 |
|
|
|
9,5 |
9,5 |
|
|
|
9,5 |
9,4 |
|
|
|
9,4 |
9,4 |
|
|
|
9,5 |
9,5 |
80 |
|
2 |
9,9 |
9,9 |
|
|
|
9,9 |
9,9 |
|
|
|
10 |
9,9 |
|
|
|
9,9 |
9,9 |
|
|
|
10 |
10 |
|
Stała siatki dyfrakcyjnej - d = 5,2±0,1 μm = 5,2*10-4±1*10-5 cm
Oszacowana wartość ∆l = 0,5 cm.
Wyznaczamy wartości średnie: hs i l
Stosujemy wzór na średnią arytmetyczną:
![]()
Barwa |
Rząd |
hs [ cm ] |
l [ cm ] |
Niebieska |
1 |
6,63 |
80 |
|
2 |
7,27 |
|
Zielona |
1 |
7,94 |
|
|
2 |
8,18 |
|
Czerwona |
1 |
9,46 |
|
|
2 |
9,93 |
|
Wyznaczamy sinusy kątów ugięcia linii.
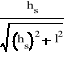
Barwa |
Rząd |
sin α |
Niebieska |
1 |
0,0828 |
|
2 |
0,0905 |
Zielona |
1 |
0,0987 |
|
2 |
0,1017 |
Czerwona |
1 |
0,1174 |
|
2 |
0,1231 |
Wyznaczamy długości poszczególnych fal
![]()
Barwa |
Rząd |
λ [μm ] |
Niebieska |
1 |
0,430 |
|
2 |
0,235 |
Zielona |
1 |
0,513 |
|
2 |
0,264 |
Czerwona |
1 |
0,610 |
|
2 |
0,320 |
Wyznaczamy średnie długości fal dla poszczególnych barw
![]()
Barwa |
λs [μm ] |
Niebieska |
0,332 |
Zielona |
0,388 |
Czerwona |
0,465 |
Obliczamy odchylenie standardowe shs oraz względne odchylenie shs/hs
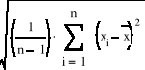
Barwa |
Rząd |
|
Niebieska |
1 |
0,021 |
|
2 |
0,021 |
Zielona |
1 |
0,044 |
|
2 |
0,016 |
Czerwona |
1 |
0,024 |
|
2 |
0,021 |
Barwa |
Rząd |
δ = shs |
shs/hs |
Niebieska |
1 |
0,048 |
0,00723 |
|
2 |
0,048 |
0,0066 |
Zielona |
1 |
0,069 |
0,00869 |
|
2 |
0,042 |
0,00513 |
Czerwona |
1 |
0,051 |
0,00539 |
|
2 |
0,048 |
0,00483 |
Obliczamy względny błąd
![]()
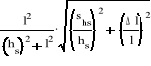
Barwa |
Rząd |
|
Niebieska |
1 |
0,9932 |
|
2 |
0,9918 |
Zielona |
1 |
0,9903 |
|
2 |
0,9896 |
Czerwona |
1 |
0,9862 |
|
2 |
0,9848 |
Obliczamy bezwzględną wartość odchylenia sλ oraz ich średnie sλs
Barwa |
Rząd |
sλ |
sλs |
Niebieska |
1 |
0,00307 |
0,00234 |
|
2 |
0,00162 |
|
Zielona |
1 |
0,00341 |
0,00257 |
|
2 |
0,00173 |
|
Czerwona |
1 |
0,00372 |
0,00281 |
|
2 |
0,00190 |
|
Zestawienie wyników pomiarów oraz obliczeń:
Barwa |
k |
hp [cm] |
hl [cm] |
hs [cm] |
shs [cm] |
l [cm] |
Δl [cm] |
λ [μm] |
λs [μm] |
sλ |
sλs |
Niebieska |
1 |
6,6 |
6,6 |
6,63 |
0,048 |
80 |
80 |
0,430 |
0,332 |
0,00307 |
0,00234 |
|
|
6,6 |
6,6 |
|
|
|
|
|
|
|
|
|
|
6,7 |
6,7 |
|
|
|
|
|
|
|
|
|
|
6,6 |
6,7 |
|
|
|
|
|
|
|
|
|
|
6,6 |
6,6 |
|
|
|
|
|
|
|
|
|
2 |
7,3 |
7,3 |
7,27 |
0,048 |
|
|
0,235 |
|
0,00162 |
|
|
|
7,3 |
7,2 |
|
|
80,5 |
|
|
|
|
|
|
|
7,2 |
7,2 |
|
|
|
|
|
|
|
|
|
|
7,3 |
7,3 |
|
|
|
|
|
|
|
|
|
|
7,3 |
7,3 |
|
|
|
|
|
|
|
|
Zielona |
1 |
8 |
7,8 |
7,94 |
0,069 |
|
|
0,513 |
0,388 |
0,00341 |
0,00257 |
|
|
7,9 |
7,9 |
|
|
|
|
|
|
|
|
|
|
7,9 |
8 |
|
|
80 |
|
|
|
|
|
|
|
8 |
8 |
|
|
|
|
|
|
|
|
|
|
8 |
7,9 |
|
|
|
|
|
|
|
|
|
2 |
8,2 |
8,2 |
8,18 |
0,042 |
|
|
0,264 |
|
0,00173 |
|
|
|
8,2 |
8,2 |
|
|
|
|
|
|
|
|
|
|
8,2 |
8,2 |
|
|
|
|
|
|
|
|
|
|
8,1 |
8,2 |
|
|
79,5 |
|
|
|
|
|
|
|
8,1 |
8,2 |
|
|
|
|
|
|
|
|
Czerwona |
1 |
9,5 |
9,4 |
9,46 |
0,051 |
|
|
0,610 |
0,465 |
0,00372 |
0,00281 |
|
|
9,5 |
9,5 |
|
|
|
|
|
|
|
|
|
|
9,5 |
9,4 |
|
|
|
|
|
|
|
|
|
|
9,4 |
9,4 |
|
|
|
|
|
|
|
|
|
|
9,5 |
9,5 |
|
|
80 |
|
|
|
|
|
|
2 |
9,9 |
9,9 |
9,93 |
0,048 |
|
|
0,320 |
|
0,0019 |
|
|
|
9,9 |
9,9 |
|
|
|
|
|
|
|
|
|
|
10 |
9,9 |
|
|
|
|
|
|
|
|
|
|
9,9 |
9,9 |
|
|
|
|
|
|
|
|
|
|
10 |
10 |
|
|
|
|
|
|
|
|
WNIOSKI:
Celem ćwiczenia było wyznaczenie długości fali świetlnej za pomocą siatki dyfrakcyjnej. Dzięki przeprowadzonym pomiarom i wykonanym obliczeniom uzyskaliśmy następujące wyniki:
λniebieska = 332 ± 2,34 [nm]
λzielona = 388 ± 2,57 [nm]
λczerwona = 465 ± 2,81 [nm]
Rachunek jest bardzo dokładny - błąd wynosi ok. 0,25 %. Jednak pomimo dokładności obliczeń otrzymane wyniki nie pokrywają się z wartościami rzeczywistymi. Pierwsze dwie fale wg. otrzymanych obliczeń byłyby niewidoczne - ich długości wskazują iż jest to ultrafiolet. Natomiast ostatnią z fal ( czyli teoretycznie czerwoną ) można zaobserwować, ale jest ona barwy niebieskiej.
Należy więc zastanowić się skąd tak duża rozbieżność wyniku otrzymanego od spodziewanych wartości, mimo iż błąd wynosił ok. 0,25%. Naszym zdaniem głównym powodem w/w różnic było niezbyt dokładne odczytanie wyników pomiarów. Spowodowane to było niezbyt dobrymi warunkami do przeprowadzenia ćwiczenia ( powinno się je wykonywać w całkowitej ciemności, aby jak najlepiej widoczne były prążki świetlne ) i być może niedokładnością skali na linijce wykorzystywanej podczas ćwiczenia laboratoryjnego.
Tak więc przeprowadzone ćwiczenie wykazało jedynie iż zgodnie z oczekiwaniami najdłuższą falą okazała się czerwona, a najkrótszą niebieska.
hs =
sin α =
λ =
λs =
δ = shs =
=
Wyszukiwarka
Podobne podstrony:
Ćwiczenie 1 Wahadło Fizyczne Wyniki Pomiarów I Wnioski
cel wykonanie wyniki pomiarow
wyniki pomiarów2 KZL3ICGUBCQYGU4HKOJFVWE5DXZOWDYALO3JWFY
wyniki pomiarów1 YWIIHA4DK44B42GMSZUNR2FRIMTMC4DFHTJZPPY
cel wykonanie wyniki pomiar
wyniki i pomiary
5 Miar pH metryczne Wyniki pomiarów
309 09, 2. Wyniki pomiar˙w: Tabela 1
jak analizować wyniki pomiarów fizyka
Znormalizowane wyniki pomiarów
wyniki pomiarów3 Z2JYWHPYMBIFKGS2JXMKKX5QZQ43BSYUPLPTGZY
wyniki?zowe pomiarów
Wyniki pomiarów masy pęczków i odpowiadających im sił zrywających 2
III WYNIKI POMIARÓW, studia mechatronika politechnika lubelska, Studia WAT, semestr 2, FIZYKA 2, LAB
Wyniki pomiarów ciepła rozpuszczania, Chemia fizyczna AGH laborki, lab 3,4
OLEJOWY PŁOMIEŃ- wyniki pomiarów, INZ-Energetyka-ECiJ, Semestr Zimowy 09-10, Spalanie i paliwa
Wyniki pomiar+-w dla ¦çwiczenia 19, chemia fizyczna, chemia, Chemia fizyczna
Wyniki pomiarów
więcej podobnych podstron