ANALIZA SYGNAŁÓW
1. Analiza sygnałów okresowych
W wyniku pomiaru, bądź też w wyniku obliczeń, wartości jakiejś wielkości fizycznej, często przedstawiamy ją w postaci funkcji obranego argumentu, a następnie w postaci wykresu. Przyjmijmy, że tym argumentem jest czas t. Taką funkcję, która przedstawia przebieg zmian danej wielkości fizycznej w czasie nazywamy sygnałem tej wielkości fizycznej. Przebieg zmian sygnału może być bardzo złożony i tym samym trudny do oceny. Gdy jest to sygnał otrzymany z pomiaru, to najczęściej nie może być opisany za pomocą elementarnych funkcji matematycznych. W przypadku, gdy jest on wynikiem obliczeń, to bywa tak złożony (np. otrzymany w postaci szeregów), że jego ocena jest również bardzo utrudniona. Dla porządku zaznaczmy, że poddajemy ocenie funkcje zdeterminowane (nie losowe). Dalej przytoczymy metody analizy tego rodzaju sygnałów, a ściślej metody ich oceny.
Często stosowanym modelem (uproszczeniem) sygnału jest sygnał okresowy. Sygnałem okresowym nazywamy taki, który spełnia następujący związek:
(1) ±nT), gdzie n=1,2,3,....
Rys.1. Przykład sygnału okresowego
Definicja ta wymaga, aby sygnał, spełniał tę zależność w przedziale −∞< t <+∞. Sygnałów nieskończenie długo trwających nie ma w przyrodzie. Dlatego sygnał okresowy jest jedynie modelem sygnałów rzeczywistych. Szczególnym przypadkiem sygnałów okresowych są sygnały harmoniczne (opisane funkcjami: sin i cos). Przykład sygnału okresowego pokazano na rys.1.
Przyjmujemy następujące nazwy: A=0.5(xmax+xmin) jest amplitudą sygnału, T jest jego okresem, ω=2π/T jest częstotliwością sygnału mierzoną w rad/s. Częstotliwość sygnału może być również mierzona w hercach [Hz]. Wówczas częstotliwość taką oznaczamy przez f=1/T. Częstotliwość f jest zazwyczaj stosowana w pomiarach sygnału. Dalej będziemy stosować głównie częstotliwość ω[rad/s].
Wiadomo, że każdą funkcję okresową, spełniającą tzw. warunki Dirichleta (w sygnałach rzeczywistych warunki te są zawsze spełnione), można przedstawić w postaci szeregu Fouriera. Szereg Fouriera stosuje się w czterech postaciach:
1) podstawowa postać szeregu
(2)
gdzie ω=2π/T [rad/s] jest podstawową częstotliwością sygnału, zaś ai i bi wyznaczamy ze wzorów:
(3)
2) kosinusowa postać szeregu
(4)
gdzie: - jest wartością średnią sygnału
(5)
3) sinusowa postać szeregu
(6)
gdzie:
(7)
nazywamy:
i-tą harmoniczną funkcji okresowej
(pierwszą harmoniczną (i=1) nazywamy harmoniczną podstawową)
dalej:
Ai nazywamy amplitudą i-tej harmonicznej,
ωi = iω -częstotliwością i-tej harmonicznej,
αi, βi -fazami początkowymi i-tej harmonicznej.
Jak więc widać, funkcję okresową można przedstawić za pomocą sumy nieskończonej liczby funkcji harmonicznych o amplitudach Ai, częstotliwościach ωi=iω oraz fazach początkowych αi lub βi;
4) zespolona postać szeregu
Weźmy pod uwagę podstawową postać szeregu Fouriera (2). Każdą harmoniczną, tj. każdy składnik sumy (2) można przedstawić następująco:
(8)
oraz
(9) ![]()
Zauważmy, że po podstawieniu (9) do (8) i wykorzystaniu tożsamości Eulera
(10) ![]()
otrzymamy:
czyli zgodnie z (8).
Wzór (2) można więc zapisać następująco:
(11)
Przyjrzyjmy się teraz wzorom (3). Z racji parzystości funkcji cos(iωt) i nieparzystości funkcji sin(iωt) względem wartości iω, możemy napisać:
więc
Pierwszą sumę we wzorze (11) można przedstawić następująco
i wzór (11) zapisać:
gdzie: . Stąd wzór powyższy przyjmuje postać:
(12)
Jest to poszukiwana zespolona postać szeregu Fouriera.
Korzystając ze wzoru (2) mamy:
(13a)
lub
(13b)
Z powyższego wzoru wyznaczamy współczynniki Ci, zwane amplitudami zespolonymi.
Na rys.2 pokazano przykłady przedstawienia za pomocą szeregu Fouriera sygnału o postaci okresowo (T=2s, ω=2π/T) powtarzających się impulsów prostokątnych. Każdy z impulsów o wartości x0=10Ns działa w ciągu τ=0.6s, czyli τ/T=0.3.
Obliczamy:
(14a)
gdzie S=x0τ,
(14b)
Rozwińmy ten sygnał w szereg Fouriera o postaci kosinusowej. Stąd
(14c)
(14d)
Jeśli podstawimy: ω=2π/T, to wyniki te można przedstawić w postaci:
(14e) ,
Po podstawieniu τ/T=0.3 mamy:
,
Praktycznie nie możemy obliczać nieskończonego szeregu Fouriera (nieskończonej sumy) i ograniczamy się do sumy skończonej liczby n składników szeregu.
Rys.2. Przykłady rozwinięcia sygnału okresowego w szeregi Fouriera
(15)
Mówimy wówczas, że zadawalamy się sumą skończonej liczby harmonicznych szeregu. Skończona suma szeregu przedstawia tylko przybliżone wartości funkcji wyjściowej, która została rozwinięta w szereg. Inaczej mówiąc funkcja okresowa zostaje wówczas aproksymowana skończoną liczbą kosinusoid o częstotliwościach będących wielokrotnością częstotliwości ω, tj. równych iω oraz o fazach początkowych αi. Oczywiście szereg nieskończony dokładnie przedstawia funkcję okresową z wyjątkiem punktów nieciągłości funkcji, w których każda z harmonicznych przechodzi przez połowę skoku funkcji (w punkcie nieciągłości).
Na rys.2 pokazano porównanie przebiegu okresowo powtarzających się imulsów oraz przybliżenie za pomocą skończonej liczby składników szeregu Fouriera (sumy skończonej). Pokazano przypadek, gdy uwzględniono 7 składników szeregu (7 harmonicznych) oraz gdy uwzględniono 20 składników szeregu (20 harmonicznych). Widać stąd, że skończony szereg tym lepiej przybliża sygnał analizowany (okresowe impulsy prostokątne) im więcej uwzględnimy składników szeregu.
Szereg Fouriera ma ważną interpretację graficzną. Weźmy pod uwagę kosinusową postać szeregu (4). Zauważmy, że aby znać w pełni szereg Fouriera, w który rozwinięto daną funkcję okresową x(t), wystarczy znać jej okres T oraz wszystkie wartości Ai i αi (dla i=0,1,2,3,...). Przedstawienie graficzne Ai i αi w funkcji ωi=iω noszą nazwę: widma sygnału okresowego.
Rys.3 Widma dyskretne sygnału okresowego
Pokazano je na rys.3 dla funkcji x(t)=5sin(3t)+2sin(6t+0.8)+10sin(9t-0.3). Rozróżniamy: widmo amplitudowo częstotliwościowe (rys.3a), w skrócie A-Cz, przedstawione za pomocą odcinków o długościach Ai i wyprowadzonych z punktów iω na osi odciętych oraz widmo fazowo-częstotliwościowe (rys.3b), w skrócie F-Cz. Jak widać, widma te składają się z dyskretnie (tj. nie w sposób ciągły) rozłożonych wzdłuż osi iω „prążków” w jednakowych odstępach. Dlatego widma te noszą nazwę widm dyskretnych.
Przykład:
Wyznaczyć widma amplitudowo-częstotliwościowe (A-Cz) i fazowo-częstotliwościowe sygnału o postaci okresowo powtarzających się impulsów prostokątnych (rys.4), gdy τ/T=1/4.
Rozwiązanie:
Na podstawie wzorów (14e) mamy:
,
Stąd otrzymujemy widma pokazane na rys.5. Zauważmy, że niektóre Ai są równe zero (np.: A4, A8, A12,...), wówczas w widmie A-Cz nie występują odpowiadające im „prążki”.
Wartości niektórych Ai, gdy udaje się je wyznaczyć analitycznie („wyciągnąć” pierwiastek), mogą wypaść ujemne - wówczas odpowiadający im „prążek” winno się odkładać po stronie ujemnej osi Ai. Zazwyczaj jednak amplitudy drgań traktuje się jako wielkości dodatnie. Wówczas widmo A-Cz budujemy dla (rys.6a). Wymaga to jednak zmiany (kompensacji) wartości faz początkowych αi. Te zmienione wartości αi oznaczamy przez. Wyznaczamy je z równości:
Rys.4. Przykład sygnału okresowego
Stąd wynika, że:
jeśli dla i=k jest Ak<0, to =αk−mπ,
jeśli dla i=k jest Ak>0, to =αk−nπ,
gdzie: m=1,3,5,..., zaś n=0,2,4,6,... Wartości m i n przyjmujemy tak, aby ≤π. Zbudowane w ten sposób widmo F-Cz pokazano na rys.6b.
Rys.5. Wyjściowe widma sygnału okresowego
Rys.6. Widmo amplitudowo-częstotliwościowe (a) i fazowo-częstotliwościowe (b)
Wysokości „prążków” widma A-Cz generalnie maleją w miarę wzrostu i. Jest to graficzne przedstawienie zbieżności szeregu Fouriera. Praktycznie pokazać możemy graficznie tylko skończoną liczbę tych „prążków”.
Na rys.7 pokazano widma A-Cz dla okresowo powtarzających się impulsów prostokątnych, lecz przy różnych wartościach τ/T. Dla dużych wartości τ/T (rys.7a) impulsy powtarzają się „często”, lecz widmo jest „rzadkie”, amplitudy kolejnych harmonicznych szybko maleją (szereg jest szybkozbieżny). Dla małych wartości
τ/T (rys.7c) jest odwrotnie i amplitudy kolejnych harmonicznych maleją powoli (szereg jest wolnozbieżny). W miarę tego jak impulsy są coraz rzadsze, widmo A-Cz staje się coraz gęstsze. Gdy T→∞, widmo z dyskretnego staje się ciągłe, co dalej będzie szerzej omówione. Na rys.5, 6 i 7 pokazano jednocześnie obwiednie widm. Zauważmy, że są one jednakowe dla wszystkich wartości τ/T. Oznacza to, że obwiednia widma zależy jedynie od kształtu impulsu, a nie od jego częstotliwości.
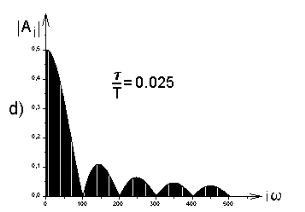
Rys.7. Widma amplitudowo-częstotliwościowe okresowych impulsów prostokątnych dla różnych τ/T.
Widma można również tworzyć dla szeregu Fouriera w postaci zespolonej. Wystarczy tutaj znać jedynie zbiór Ci (i=0, ±1, ±2, ±3,....), tj. zespolonych amplitud poszczególnych harmonicznych szeregu. Skoro każdą liczbę zespoloną możemy przedstawić za pomocą dwóch liczb rzeczywistych ![]()
(![]()
), przeto widma możemy zbudować według dwóch wariantów:
1) widma budujemy w postaci „prążków” osobno dla ![]()
i osobno dla ![]()
. Pierwsza z nich nosi nazwę części rzeczywistej widma zespolonego (rys.8a), druga zaś części urojonej widma zespolonego (rys.8b).
![]()
2) korzystamy z postaci: ![]()
, gdzie
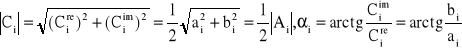
Widma budujemy w postaci „prążków” osobno dla Ci , które nosi nazwę modułu widma zespolonego (rys.8c) i osobno dla αi, które nosi nazwę fazy widma zespolonego (rys.8d). Na rys.8 przedstawiono komplet widm zespolonych dla przykładu 1. Zauważmy, że część rzeczywista widma zespolonego jest zawsze parzysta względem iω, zaś część urojona -nieparzysta. Podobnie moduł widma zespolonego jest zawsze parzysty względem iω, zaś faza -nieparzysta.
Przedstawiona analiza funkcji okresowych może być również zastosowana do szczególnego przypadku funkcji nieokresowej, zwanej poliharmoniczną, np.
![]()
Otrzymamy wówczas również widmo „prążkowe”, lecz odległości między „prążkami” nie będą jednakowe, jeśli ωi ≠iω. Funkcje poliharmoniczne ogólnie nie są okresowe. Jedynie w przypadku, gdu zachodzi związek
gdzie r1, r2,..., rn są liczbami współmiernymi, funkcja ta jest okresowa.
Rys.8. Widma zespolone sygnału o postaci okresowych impulsów prostokątnych.
2. Analiza sygnałów nieokresowych
Do analizy takich sygnałów nie możemy stosować szeregów Fouriera. Miejsce szeregu Fouriera zajmuje tutaj całka Fouriera, która może być zdefiniowana matematycznie jako pewne przekształcenie całkowe funkcji czasu (transformacja całkowa), lecz można ją również wyprowadzić, może niezbyt formalnie matematycznie, ale na drodze bardzo poglądowego rozumowania fizycznego, podanego w książce: ** ** *****************************************************
Funkcję nieokresową możemy mianowicie uważać za graniczny przypadek funkcji okresowej, gdy jej okres zmierza do nieskończoności (rys.9). Spróbujmy zatem dokonać przejścia granicznego szeregu Fouriera, gdy okres sygnału nieograniczenie rośnie.
Weźmy pod uwagę sygnał okresowy i odpowiadający mu szereg Fouriera w postaci zespolonej:
![]()
gdzie:
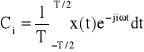
co można zapisać następująco:
(16) 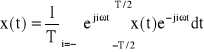
Rys.9. Przykład funkcji nieokresowej
W miarę tego jak okres T rośnie, przy nie zmieniającym się impulsie (τ=const), „prążki” widma zagęszczają się (rys.7), tj. odległości między „prążkami” maleją. Oznaczmy te odległości przez Δω. Zatem ![]()
. Wartości częstotliwości odpowiadających poszczególnym „prążkom” oznaczymy przez ωi, więc ωi=iω. Wówczas wzór (16) można zapisać następująco:
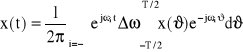
Gdy T→∞, to ωi →ω, gdzie ω oznacza teraz częstotliwość bieżącą, zaś suma w powyższym wzorze zmierza do całki. W granicy otrzymamy:
(17) 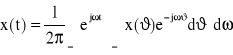
Oznaczmy
(18) 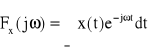
Stąd, na podstawie (17) mamy:
(19) 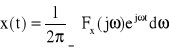
Wzory (18) i (19) są podstawowymi wzorami tzw. metod spektralnych (widmowych) w analizie sygnałów. Przedstawiają one parę przekształceń całkowych Fouriera, wiążących ze sobą dwie funkcje: rzeczywistą funkcję czasu x(t) i zespoloną funkcję częstotliwości. Wzory (18) i (19) są jednocześnie podstawowymi wzorami rachunku operatorowego Fouriera: funkcja x(t) jest oryginałem, zaś jest jego „obrazem” lub inaczej transformatą lub też przekształceniem całkowym. (Zauważmy, że przekształcenie Fouriera jest szczególnym przypadkiem ogólniejszego przekształcenia, a mianowicie przekształcenia całkowego Laplace'a
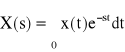
gdzie s=h+jω. Gdy h=0 przekształcenie Laplace'a staje się przekształceniem Fouriera. Przekształcenie Fouriera może być wprawdzie dokonane na węższej klasie funkcji niż przekształcenie Laplace'a, lecz ma tę wyższość, że możemy mu nadać jasny sens fizyczny).
Wzajemną relację funkcji x(t) i jej przekształcenia całkowego Fouriera ![]()
określoną wzorami (18) i (19) oznaczamy symbolicznie
![]()
Operację całkową na funkcji x(t) według wzoru (18) nazywamy transformacją Fouriera funkcji x(t) (symbol FT -Fourier Transform) lub transformatą wprost, zaś ![]()
-transformatą funkcji x(t). Operację całkową na funkcji ![]()
według wzoru (19) nazywamy transformacją odwrotną Fouriera (względem (18)) (symbol IFT -Inverse Fourier Transform) lub retransformatą funkcji ![]()
.
Porównajmy wzór (19) dotyczący funkcji nieokresowej ze wzorem (12) przedstawiającym rozwinięcie funkcji okresowej xo(t) w szereg Fouriera o postaci zespolonej
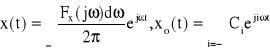
Jeśli szereg Fouriera przedstawia funkcję okresową xo(t) w postaci nieskończonej sumy harmonicznych, mających skończone wartości amplitud zespolonych Ci i dyskretnie rozłożone wartości częstotliwości, to całka (19) przedstawia funkcję nieokresową x(t) w postaci „sumy” (całki) funkcji harmonicznych, lecz o nieskończenie małych amplitudach zespolonych: ![]()
oraz częstotliwościach rozłożonych wzdłuż osi ω w sposób ciągły. Interpretacja ta stanie się jeszcze bardziej zrozumiała, gdy przekształcimy wzory (18) i (19) do postaci rzeczywistych.
Przedstawmy następująco:
(20) ![]()
gdzie
(21) 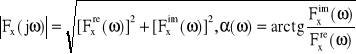
Podstawmy (20) do (19)
(22) 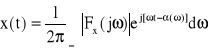
Na mocy tożsamości Eulera mamy:
![]()
Stąd wzór (22) można zapisać następująco:
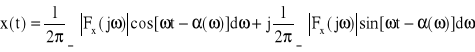
Moduł ![]()
jest funkcją parzystą względem ω, tj.
![]()
=![]()
Dla pozostałych funkcji mamy:
![]()
oraz
![]()
-parzysta
![]()
-nieparzysta.
Stąd
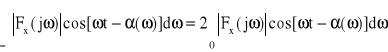
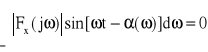
i wzór (22) przyjmie postać analogiczną do kosinusowej postaci szeregu Fouriera
(23) 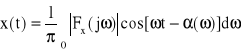
Porównując wzór (23) dla funkcji nieokresowej x(t) ze wzorem przedstawiającym rozwinięcie funkcji okresowej xo(t) w szereg Fouriera w postaci kosinusowej dochodzimy do podobnej analogii jak dla postaci zespolonych.
Obok nazw wyżej podanych, wywodzących się z rachunku operatorowego stosujemy również inne. Nazywamy:
![]()
-zespoloną gęstością widmową sygnału x(t),
![]()
-amplitudową gęstością widmową sygnału x(t),
α(ω) -fazową gęstością widmową funkcji x(t).
Wymienione funkcje noszą nazwę gęstości widmowych, gdyż we wzorze (23) wielkość ![]()
można interpretować jako pochodną amplitudy ![]()
względem ω. W związku z tym, o ile amplitudy Ai mają te same miana co xo(t), o tyle ![]()
ma inne miano niż x(t), a mianowicie miano x podzielone przez miano ω. Na przykład, gdy x mierzymy w [m], to ![]()
mierzymy w [ms].
Sygnały okresowe miały widma „prążkowe”, czyli widma dyskretne. Funkcje nieokresowe charakteryzujemy gęstościami widmowymi, które są funkcjami ciągłymi, a więc mają widma ciągłe. Dlatego, w celu skrócenia nazewnictwa, częst opuszczamy słowo „gęstość” i mówimy krótko: „widma ciągłe”.
Wcześniej wspomniano, że funkcje okresowe rozwijane w szereg Fouriera winny spełniać tzw. warunki Dirichleta. Transformata Fouriera (18) również wymaga, aby funkcja x(t) spełniała te warunki. Warunki te podaje literatura poświęcona szeregom i człkom Fouriera. Tutaj jedynie zaznaczymy, że sygnały fizyczne warunki takie zawsze spęłniają.
Przykład:
Przedstawić gęstości widmowe impulsu prostokątnego o wartości S=xoτ (jak na rys.9).
Rozwiązanie:
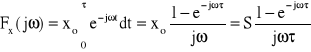
Powyższy wynik przekształcamy oddzielając część rzeczywistą od urojonej
![]()
Rys.10. Gęstości widmowe (transformaty Fouriera) impulsu prostokątnego.
Stąd (patrz wzór (20)):
![]()
oraz
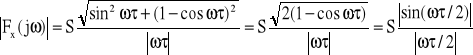
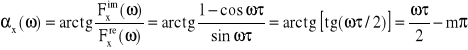
Zestaw gęstości widmowych pokazano na rys.10. Biorąc pod uwagę, że wykresy tych widm są albo funkcjami parzystymi (rys.10a i c) albo nieparzystymi (rys.10b i d) względem ω, często rysuje się jedynie ich część dla ω≥0.
Przykład:
Wyznaczyć moduł gęstości widmowej impulsu o postaci skończonej liczby n (n=1, 2, 3,...) połówek sinusoidy.
Rozwiązanie.
Sygnał ten można zapisać następująco:
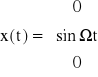
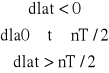
gdzie ![]()
.
Stąd mamy:
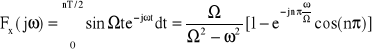
Dla n nieparzystych otrzymamy:
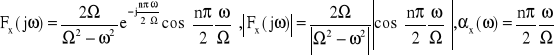
Dla n parzystych otrzymamy:
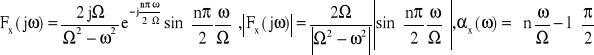
Moduły gęstości widmowych impulsów w postaci różnej liczby połówek sinusoid pokazano na rys.11. Z rysunku tego widać jak w miarę wzrostu liczby n półokresów formuje się część główna widma w otoczeniu ω=Ω.
Przykład:
Wyznaczyć moduł gęstości widmowej sygnału (swobodne drgania układu liniowego o jednym stopniu swobody): ![]()
przy t>0.
Rozwiązanie
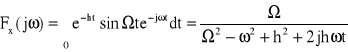
Stąd
, ![]()
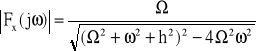
, ![]()
Moduł gęstości widmowej sygnału pokazano na rys.12.
Rys.11.Gęstości widmowe (transformaty Fouriera) odcinków sinusoidy.
Rys.12. Gęstości widmowe wykładniczo zanikającego sygnału oscylacyjnego.
3. Funkcje uogólnione (pseudofunkcje, dystrybucje)
W obliczeniach dotyczących analizy sygnałów często dogodnie, szczególnie w części dowodowej, dogodne jest korzystanie z funkcji uogólnionych. Nie będziemy tu zajmować się teorią dystrybucji, gdyż poświęcone są jej liczne monografie. Własności funkcji uogólnionych przedstawimy za pomocą przejścia granicznego odpowiednio dobranych funkcji ciągłych (patrz ********************** *************************************************). Weźmy pod uwagę funkcję (rys.13)
(24a) ![]()
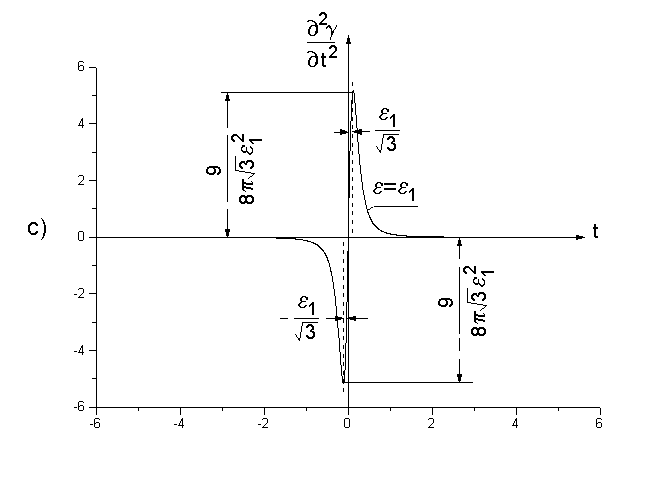
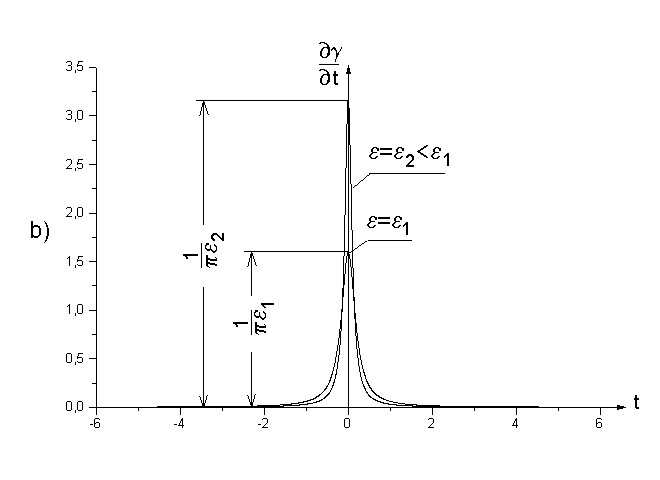
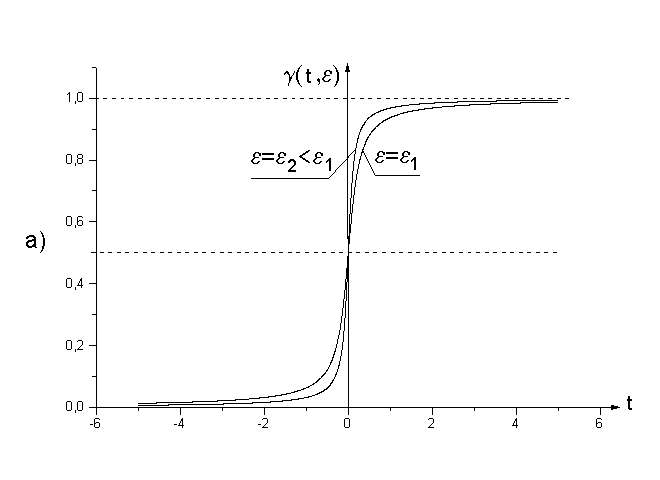
(24b) 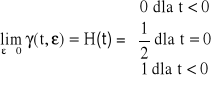
Rys.13. Przejście graniczne do funkcji uogólnionych.
H(t) nazywamy funkcją Heaviside'a lub funkcją skoku jednostkowego.
Funkcję γ(t,ε) możemy różniczkować względem t (rys.13b,13c).
![]()
,
(25) 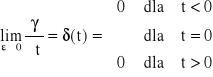
δ(t) nazywamy „delta” funkcją Diraca.
(26) 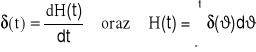
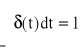
Podobnie:
(27) ![]()
Funkcja ![]()
nosi nazwę „dipol”.
Funkcje H(t) i δ(t) dla argumentów przesuniętych o θ są następujące (rys.14):
(28) 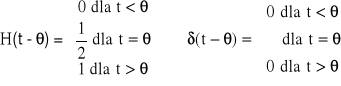
oraz
(29) 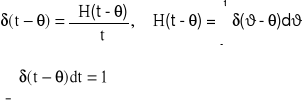
Niektóre własności „delta” funkcji Diraca [gdy f(t) jest funkcją ciągłą]
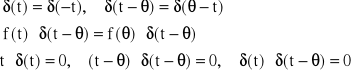
(30) 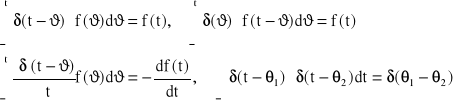
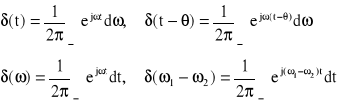
Rys.14. Symboliczne oznaczenia funkcji uogólnionych
Transformaty Fouriera funkcji uogólnionych
1. „delta” funkcja Diraca (rys.15)
![]()
.
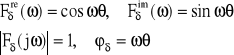
2. Funkcja skoku jednostkowego (rys.15)
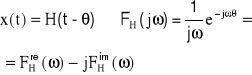
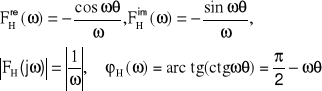
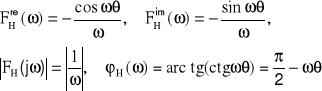
3. Funkcja stała
Jako funkcję stałą rozumiemy x(t)=C w całym przedziale czasu od ![]()
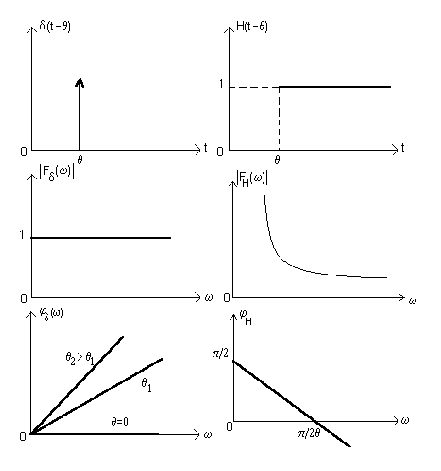
Rys.15. Transformaty Fouriera funkcji uogólnionych
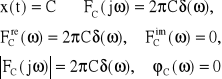
4. Funkcja harmoniczna (rys.16)
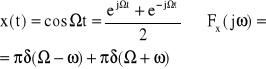
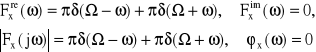
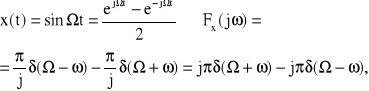
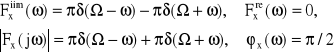
Rys.16. Transformaty Fouriera funkcji harmonicznych
4. Ocena sygnałów
W wyniku pomiaru, bądź też w wyniku obliczeń, wartości jakiejś wielkości fizycznej, często przedstawiamy ją w postaci funkcji określonego lub obranego argumentu, a następnie w postaci wykresu. Przyjmijmy, tym argumentem jest czas t. Taką funkcję, która przedstawia przebieg zmian danej wielkości fizycznej w czasie nazywamy sygnałem tej wielkości fizycznej. Przebieg zmian sygnału może być bardzo złożony i tym samym trudny do oceny. Gdy jest to sygnał otrzymany z pomiaru, to najczęściej nie może być opisany za pomocą elementarnych funkcji matematycznych. W przypadku, gdy jest on wynikiem obliczeń, to bywa tak złożony (np. otrzymany w postaci szeregów), że jego ocena jest również bardzo utrudniona. Dla porządku zaznaczmy, że poddajemy ocenie funkcje zdeterminowane (nie losowe). Dalej przytoczymy metody analizy tego rodzaju sygnałów, a ściślej metody ich oceny. Przedtem jednak zauważmy, że w przypadku pomiaru sygnału, mamy do czynienia nie z funkcją (sygnałem) w dowolnie dużym zakresie czasu, lecz w skończonym przedziale czasu, tj. na odcinku pomiarowym T. Często i w przypadku sygnału obliczonego zadawalamy się oceną jego odcinka w skończonym przedziale czasu. Taką funkcję (w skończonym przedziale czasu) nazwiemy umownie funkcją skończoną (finite function, ***************). Weźmy pod uwagę rys.17. Pokazano na nim przebieg pewnego sygnału x(t) w przedziale czasu -T/2< t <T/2 (nie ma znaczenia, czy rozważamy taki przedział czasu czy też 0<t<T). Skoro dany sygnał obserwujemy tylko w tym przedziale czasu i nie wiemy jaki jest jego przebieg poza tym przedziałem przeto przyjmujemy, że:
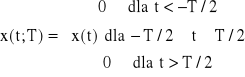
Oczywiście:
![]()
Z formalnego punktu widzenia ważne są następujące równości:
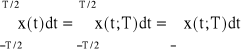
Dalej, dla uproszczenia pisowni, będziemy pomijać w zapisie x(t;T) symbol T przedziału obserwacji sygnału, tj. będziemy zapisywać:
![]()
Rys.17. Przykład funkcji skończonej.
Z formalnego punktu widzenia ważne są następujące równości:
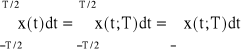
Dalej, dla uproszczenia pisowni, będziemy pomijać w zapisie x(t;T) symbol T przedziału obserwacji sygnału, tj. będziemy zapisywać:
![]()
Wymienimy teraz najczęściej stosowane oceny sygnałów (tzw. estymatory):
a) Wartość średnia
(31) 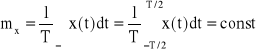
b) Funkcja korelacji własnej
(32) 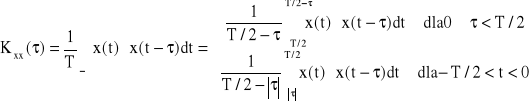
lub
(33) 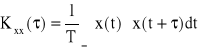
Funkcja korelacji własnej jest parzysta względem τ:
(34) ![]()
c) Wariancja
(35) 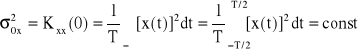
d) Wartość skuteczna (RMS -Root Mean Square)
(36) 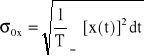
e) Funkcja centralna (Odchylenie od wartości średniej)
(37) ![]()
f) Funkcja kowariancji własnej
(38a) 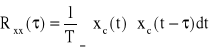
lub
(38b) 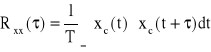
zatem
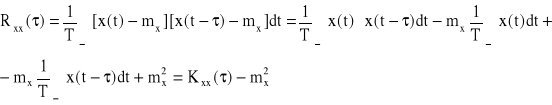
g) Wariancja centralna
(39) ![]()
h) Średnie odchylenie standardowe
(40) ![]()
i) Funkcja korelacji wzajemnej dwóch sygnałów: x(t) i y(t)
(41) 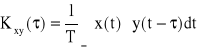
j) Funkcja korelacji odwrotnej dwóch funkcji
(42) 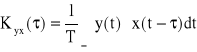
oraz
(43) ![]()
To ostatnie wynika to z następującego: Zmieńmy zmienną całkowania; t=ϑ+τ. Wówczas
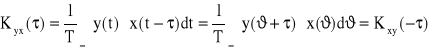
21
J. W. Osiecki: Analiza sygnałów.
![]()
Rys.11
Wyszukiwarka
Podobne podstrony:
Lab5 Analiza sygnalu mowy Lab5 Nieznany
Oceny Analiza sygnałów
Analiza sygnałów projekt
Analiza sygnalow i predykcja cz 1
analizasygnalowiidentyfikacja2, Analiza sygnałów
lab 4 chuso, Mechatronika AGH IMIR, semestr 6, Identyfikacja i analiza sygnałów 2, lab4
IiAS lab 1, Mechatronika AGH IMIR, semestr 6, Identyfikacja i analiza sygnałów 2, sprawozdania
Techniki analizy sygnału mowy, Wisniewski.Andrzej, Analiza.Obrazow.I.Sygnalow, Materialy
Analiza sygnałów i identyfikacja
Analiza i identyfikacja sygna, Mechatronika AGH IMIR, semestr 6, Identyfikacja i analiza sygnałów 2,
Analiza Sygnałów i Identyfikacja
Projekt Zaliczeniowy(1), AGH IMIR AiR, Analiza sygnałów, analiza 2
2 Analiza sygnalu
Analiza sygnalow i predykcja cz 2
w.06-analiza sygnalow, Polibuda, Semestr V, Kompatybilnosc Elektromagnetyczna, Wykład
1B Przetworniki Sig, Wojskowa Akademia Techniczna (WAT), Analiza Sygnałów, Wykłady, Piotrowski Zbign
Analiza sygnału silnika (MECH) TW1
Cw 3 analiza sygnalow w dziedzinie czestotliwosci
więcej podobnych podstron