ANALIZA SYGNAŁÓW I IDENTYFIKACJA - SPRAWOZDANIE Z ĆWICZEŃ LABORATORYJNYCH Prowadzący: dr inż. Marcin Nawrocki Rok akademicki 2009/20010, semestr zimowy
Piotr RAJDA	Grupa. 18b

LABORATORIUM 5 i 6

Wyznaczanie transmitancji nieznanego obiektu na podstawie charakterystyki amplitudowo-fazowej i odpowiedzi skokowej.

1.Teoria

1.1 Metoda transformaty Fouriera

1.2.1 Wyznaczanie transmitancji układu na podstawie jego odpowiedzi skokowej - sposób I.

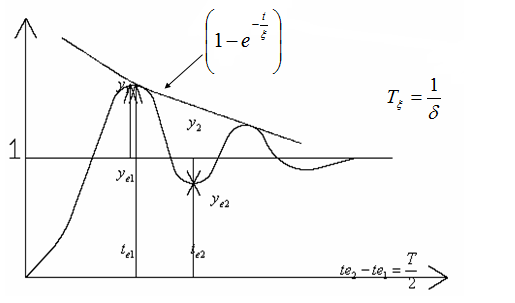
Ekstrema y(t) - obliczamy dy/dt i przyrównujemy do zera. Występują dla t_e=kπ/2;

k=0,1,2… podstawiając t_e1 i t_e2 do równania y(t) otrzymujemy y₁ i y₂.

1.2.1 Wyznaczanie transmitancji układu na podstawie jego odpowiedzi skokowej - sposób II.

Transmitancje elementu oscylacyjnego II rzędu ma postać:

.

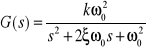
Czasową odpowiedź elementu na pobudzenie skokiem jednostkowym wyraża zależność:

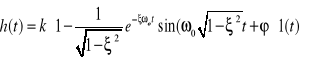
Przebieg h(t) przedstawia wykres:

Wartość współczynnika k można obliczyć bezpośrednio z wykresu funkcji h(t), natomiast pozostałe stałe z zależności:

2.Pomiary

2.1 Określenie transmitancji obiektu 2 rzędu na podstawie charakterystyki amplitudowo-fazowej.

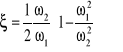
Kod programu z komentarzami:

dt=0.01; %czas probkowania

t=0:0.01:999.99;

t=t'; %przetransponowany wektor czasu

L=50 %licznik transmitancji

M=[1 5 50] %mianownik transmitancji

g=tf(L,M); %przypisanie transmitacji pod zmienna

x=rand(size(t))-0.5; %szum sygnal wejsciowy

y=lsim(g,x,t); %symulacja odpowiedzi czasowej modelu g typu LTI

Fx=fft(x); %szybka transformata fouriera wektora x

Fy=fft(y); %szybka transformata fouriera wektora y

Pxx=Fx.*conj(Fx); %likwidacja czesci rojonej

Pxy=conj(Fx).*Fy; %likwidacja czesci urojonej

mod=Pxy./Pxx; %charakterystyka czestotliwosciowa

mod2=decimate(mod,10); %usrednienie wartosci

figure(1);

plot(mod2(1:500)) %charakterystyka amplitudowo-fazowa

grid on;

Ns=(1000/dt)*0.1; %ilosc elementow

df=1/(dt*Ns)

w1=78*df*2*pi; %czestotliwosc punktu charakterystycznego 1

w2=111*df*2*pi; %czestotliwosc punktu charakterystycznego 2

T0=1/w2; %wspolczynniki transmitancji

z=w2/2/w1*(1-w1^2/w2^2);

gi=tf(1,[T0^2 2*z*T0 1])

figure(3);

step(g,gi) %wykres porownujacy odpowiedzi skokowe otrzymanych na podstawie

%transmitancji zadanej i wyznaczonej z transformaty fouriera

legend('zadana','wyznaczona');

Transmitancja obiektu:

Transmitancja otrzymana z transformaty Fouriera:

Maksymalny błąd względny bmax=2.81%

2.2 Określenie transmitancji obiektu 3 rzędu na podstawie charakterystyki amplitudowo-fazowej.

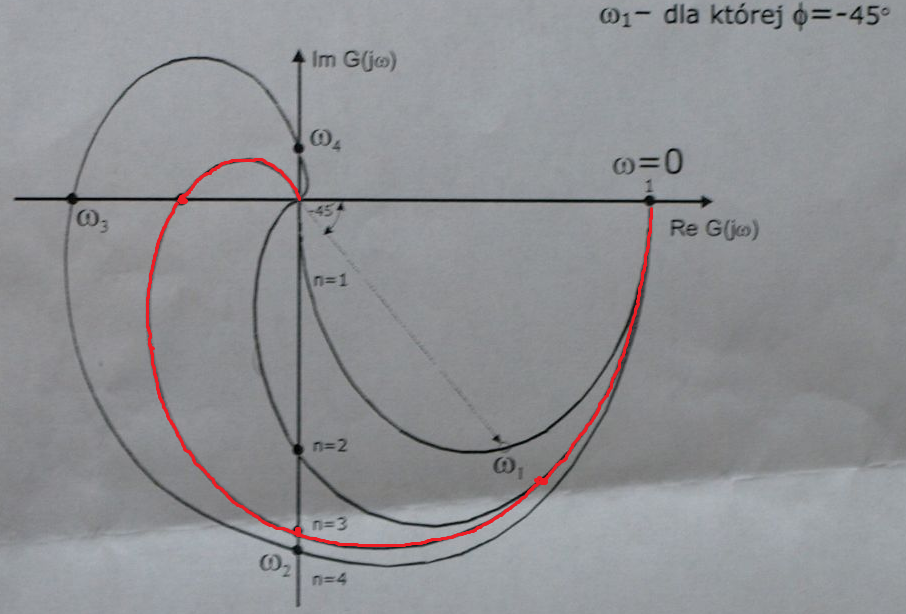
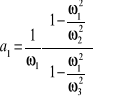
Kod programu z komentarzami:

dt=0.01; %czas probkowania

t=0:0.01:999.99;

t=t'; %przetransponowany wektor czasu

L=12 %licznik transmitancji

M=[3 5 9 13] %mianownik transmitancji

g=tf(L,M); %przypisanie transmitacji pod zmienna

x=rand(size(t))-0.5; %szum sygnal wejsciowy

y=lsim(g,x,t); %symulacja odpowiedzi czasowej modelu g

%typu lti i przypisianie zmiennej

Fx=fft(x); %szybka transformata fouriera wektora x

Fy=fft(y); %szybka transformata fouriera wektora y

Pxx=Fx.*conj(Fx); %likwidacja czesci rojonej

Pxy=conj(Fx).*Fy; %likwidacja czesci urojonej

mod=Pxy./Pxx; %charakterystyka czestotliwosciowa

mod2=decimate(mod,4); %usrednienie wartosci

figure(1);

plot(mod2(1:500)) %charakterystyka amplitudowo-fazowa

grid on;

Ns=(1000/dt)*0.25 %ilosc elementow

df=1/(dt*Ns)

w1=49*df*2*pi; %czestotliwosc punktu charakterystycznego 1

w2=64*df*2*pi; %czestotliwosc punktu charakterystycznego 2

w3=69*df*2*pi; %czestotliwosc punktu charakterystycznego 3

a1=(1/w1)*((1-((w1^2)/(w2^2)))/(1-((w1^2)/(w3^2)))) %wspolczynniki transmitancji

a2=1/(w2^2)

a3=a1/(w3^2)

gi=tf(1,[a3 a2 a1 1])

figure(2);

step(g,gi) %wykres porownujacy odpowiedzi skokowe otrzymanych na podstawie

%transmitancji zadanej i wyznaczonej z transformaty

%fouriera

legend('zadana','wyznaczona');

Transmitancja obiektu:

Transmitancja otrzymana z transformaty Fouriera:

Maksymalny błąd względny bmax=9.82%

2.3 Określenie transmitancji obiektu 2 rzędu na podstawie odpowiedzi skokowej - metoda I.

Kod programu z komentarzami:

dt=0.01; %czas probkowania

t=0:dt:499*dt; %wektor czasu

Lr=50; %licznik transmitancji

Mr=[1,5,50]; %mianownik transmitancji

Gr=tf(Lr,Mr); %przypisanie transmitacji pod zmienna

N=500 %ilosc probek

[y,ts]=step(Gr,t,[0:dt:N*dt-dt]); %odpowiedź skokowa ukladu

grid on

[y1,n1]=max(y); %znalezienie maksimum

y1=y1-1;

[y2,n2]=min(y(n1:500)); %znalezienie minimum

y2=1-y2;

z=log(y1/y2)/sqrt(pi^2+log(y1/y2)^2); %obliczanie parametrow potrzebnych

%do znalezienie transmitacji

T=2*n2*0.01;

w=2*pi/T;

d=z*w/sqrt(1-z^2);

w0=sqrt(w^2-d^2);

T0=1/w0;

gi=tf(1,[T0^2,2*z*T0,1]); %tworzenie transmitancji

step(Gr,gi,'r') %wykres porownujacy odpowiedzi skokowe otrzymanych na podstawie transmitancji zadanej i wyznaczonej

legend('zadana','wyznaczona');

Transmitancja obiektu:

Transmitancja otrzymana z odpowiedzi skokowej

Maksymalny błąd względny bmax=29.32%

2.4 Określenie transmitancji obiektu 2 rzędu na podstawie odpowiedzi skokowej - metoda II.

Kod programu z komentarzami:

dt=0.01; %czas probkowania

t=0:dt:dt*499; %wektor czasu

L=50; %licznik transmitancji

M=[1,5,50]; %mianownik transmitancji

G=tf(L,M); %przypisanie transmitancji pod zmienna

N=500; %ilość próbek

[y,ts]=step(G,t); %odpowiedź skokowa układu

[y1,t1]=max(y); %wyszukiwanie pierwszego maksima

y1=y1-1;

[y3,t3]=min(y(t1:end));

[y2,t2]=max(y((t1+t3):end));%wyszukanie drugiego maksima

y2=y2-1;

t2=(t1+t2+t3)*dt

t1=t1*dt

T=t2-t1 %obliczenie okresu oscylacji

w=2*pi/T; %obliczenie współczynników transmitancji

a=1/T*log(y1/y2);

w0=sqrt(w^2+a^2)

E=a/w0;

L1=w0^2 %licznik transmitancji

M1=[1,2*E*w0,w0^2] %mianownik transmitancji

G1=tf(L1,M1); %przypisanie transmitancji do zmienna

step(G,G1)

legend('zadana','wyznaczona')

Transmitancja obiektu:

Transmitancja otrzymana z odpowiedzi skokowej

Maksymalny błąd względny bmax=2.07%

3. Porównanie dokładności metod służących do określenie transmitancji obiektów oraz wnioski

Wnioski:

Na podstawie przeprowadzonych procedur jesteśmy w stanie zaobserwować że metody służące do określania transmitancji obiektów nadają się do przeprowadzanych działań, choć dają różne efekty.

Błędy względne dla metody wykorzystującej odpowiedzi skokowe II (max1 i max2) są bardzo małe i nie przekraczają 3%, dla metody wykorzystującej transformatę Fouriera nie przekraczają 10%, a dla metody wykorzystującej odpowiedzi skokowe I (maks i min) nie przekraczają 30%. Metody te sprawdzają się również w przypadkach układów wyższych rzędów, ale należy pamiętać że nie pozwalają na idealne odtworzenie transmitancji, oraz na uzyskanie rzeczywistego wzmocnienia układu. Metody te są też bardzo podatne na zmiany ilości próbek, oraz wpływają na nie inne zaokrąglenia i uproszczenia zastosowane w programie. Zastanawiając się nad wyborem metody identyfikacji obiektu, musimy zdecydować się jak dokładna identyfikacja jest nam potrzebna.

---