WFiIS	1. Dominik Kućma 2. Adam Skorek		Rok 2	Grupa : 2	Zespół: 11
Pracownia Fizyczna 2	Temat: Dyfrakcja światła na szczelinie				Nr ćw. 124
Data wykonania: 21.03.2007	Data oddania: 28.03.2007	Zwrot do poprawy:	Data oddania:	Data zaliczenia:	OCENA:

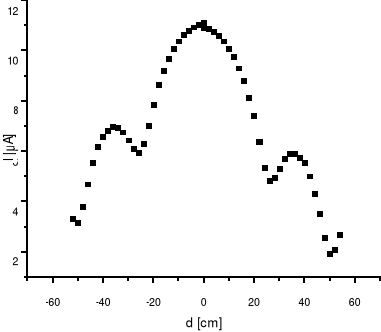
Posiadając wykres natężenia światła od położenie elementu światłoczułego jesteśmy w stanie wyznaczyć szerokość szczeliny oraz odległość pomiędzy szczelinami.

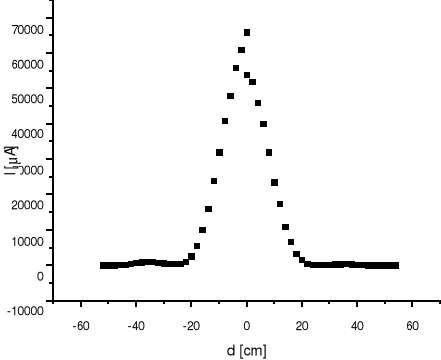
Dużą różnicę w maksimum dla strony lewej i prawej tłumaczy wysoki zakres na jaki była ustawiona miarka, nie wykluczam również błędu grubego spowodowanego np. zaświeceniem światła na sąsiednim stanowisku.

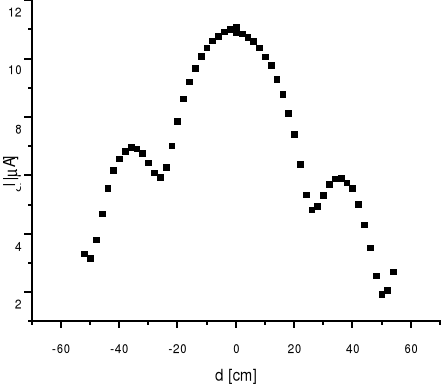
Z tego wykresu też będę odczytywał położenie minimów i maksimów.

	poł. z lewej	Poł. z prawej	x=(x2+x1)/2
	x1 [cm]	X2 [cm]
1 min	-0,0026	0,0024	0,0025
1 max	-0,0036	0,0036	0,0036
2 min	-0,0050	0,0050	0,0050

Znając średnie położenie minimów i maksimów obliczam szerokość szczeliny, korzystając ze wzorów:

Dla minimum:

dla maksimum

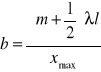
gdzie l to odległość od szczeliny (l=1,17 m), lambda to długość fali (λ=670*10^-9 m), a x to odległość ekstremum od środka.

	poł. z lewej	Poł. z prawej	x=(x2+x1)/2	Szer. szczeliny
	x1 [cm]	X2 [cm]		a [m]
1 min	-0,0026	0,0024	0,0025	0,31E-03
1 max	-0,0036	0,0036	0,0036	0,33E-03
2 min	-0,0050	0,0050	0,0050	0,31E-03

b_śr=0,32*10^-3 m; odchylenie standardowe σ_b =0,0075*10^-3 m

b = 0,32 + 0,01 [m*10^-3]

Wnioski:

Pomimo rozbieżności dla centralnego maksimum, wyliczone wartości szerokości szczeliny dla poszczególnych ekstremów nie różnią się znacznie. Pozwoliło mi to na wyznaczenie szerokości szczeliny z bardzo dużą dokładnością. Rezultaty byłyby lepsze, gdyby udało się uzyskać obraz kolejnych ekstremów, niestety natężenie wiązki było zbyt małe, żeby miarka mogła ją wychwycić.