Statystyka matematyczna 2010 (duża próba)

W celu zbadania średnich wysokości sumy ubezpieczenia na życie wylosowano 41 klientów poniżej 30 roku życia i 41 w wieku 30 lat i starszych w firmie ubezpieczeniowej Z i na podstawie tych prób uzyskano następujące wyniki

S₁=12 tyś zł.

S₂=17 tyś zł.

1. Przeprowadź estymację średniej sumy ubezpieczenia osób poniżej 30 roku życia.

1. Jakiego parametru dotyczy estymacja?

2. Czym jest ten parametr (liczbą, zmienną losową)?

3. Podaj nazwę estymatora szacowanego parametru.

4. Podaj właściwości stosowanego estymatora i jego rozkład.

5. Czym jest estymator (liczbą, zmienną losową)?

6. Oblicz oceny parametrów na podstawie wylosowanej próby.

7. Oblicz błąd standardowy szacunku.

8. Przeprowadź estymację punktową szacowanego parametru.

9. Załóż wysokość współczynnika ufności.

10. Odczytaj z tablic rozkładu estymatora wartość statystyki.

11. Oblicz maksymalny błąd szacunku.

12. Przeprowadź estymację przedziałową szacowanego parametru.

13. Zakładając, że powyższa próba jest próbą pilotażową, wyznacz minimalną liczebność próby przy wsp. ufności 0,95, taką aby maksymalny błąd szacunku był nie większy niż:

2 tyś. zł. (przedział ufności nie szerszy niż 4 tyś zł.)

1. Estymacja dotyczy średniej (arytmetycznej) wysokości sumy ubezpieczenia w populacji.

2. Parametr jest nieznaną szacowaną liczbą.

3. Najlepszym estymatorem jest średnia z próby.

4. Jest to estymator nieobciążony, zgodny, najbardziej efektywny. Ponieważ nie znamy odchylenia standardowego w populacji, więc dokładnym rozkładem estymatora jest rozkładem t-Studenta o n-1 stopniach swobody, w przypadku dużej próby zamiast rozkładu t-Studenta korzystamy z asymptotycznego rozkładu normalnego.

5. Estymator jest zmienną losową.

6. 
   
   

7. 
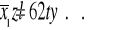
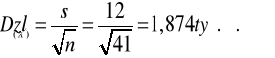
   Średnie z prób 41 elementowych różnią się średnio od średniej w populacji o 1,874 tyś zł. Średni błąd, jaki będziemy popełniać szacując średnią przy powyższych warunkach wynosi 1,874 tyś zł.

8. Zakładamy, że średnia w populacji jest równa ocenie z próby. Ocenę uzupełniamy błędem standardowym szacunku.
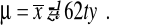
   Przy błędzie standardowym szacunku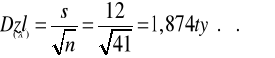
   

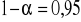
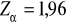
9. 
   

10. 
    

11. Maksymalny błąd szacunku obliczamy mnożąc standardowy błąd szacunku przez
    

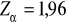
12. Od oceny z próby odejmujemy maksymalny błąd (dolna granica przedziału) i do oceny z próby dodajemy maksymalny błąd (górna granica przedziału).

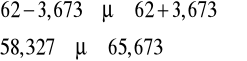
Przedział o końcach 58,327 tyś zł i 65,673 tyś zł przy współczynniku ufności 0,95 obejmie nieznaną szacowaną średnią wysokość sumy ubezpieczenia w całej populacji.

13.

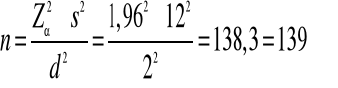
2. Na podstawie powyższych prób sprawdź hipotezy o jednakowym zróżnicowaniu i jednakowym średnim poziomie sumy ubezpieczenia w obu zbiorowościach ubezpieczonych przy poziomie istotności α=0,05.

H₀:

H_!:

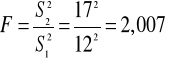
F_α=1,69

Wniosek:

Hipotezę o jednakowych wariancjach odrzucamy.

H₀:

H_!:

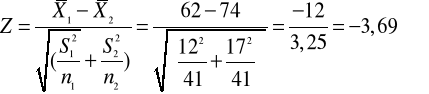
Z_α=1,96

Wniosek: Hipotezę zerową odrzucamy.

5. Co oznacza zapis: „N( 20;5)” …Rozkład normalny o średniej 20 i odchyleniu standardowym 5.

6. Co to jest „poziom istotności”. Prawdopodobieństwo popełnienia błędu I go rodzaju

7. Podaj definicję dystrybuanty Prawdopodobieństwo, że zmienna losowa przyjmie wartość poniżej X

8. Czym charakteryzuje się estymator nieobciążony. Szacuje parametr bez błędu systematycznego.

---