WSTĘP

Lepkość jest własnością gazów i cieczy. Charakteryzuje ona ich opór podczas płynięcia wywołanego siłami zewnętrznymi. Zjawisko to bywa także nazywane tarciem wewnętrznym. W ciałach stałych tarcie to jest oporem przeciwko powstawaniu odkształceń stycznych. Właściwość ta mierzona jest ilościowo współczynnikiem lepkości lub też w skrócie lepkością.

Rozpatrzmy teraz przepływ cieczy rzeczywistej przez przewód o przekroju poprzecznym r₀ i długości l₀. Przyjmiemy, że siła lepkości cieczy F jest proporcjonalna do gradientu prędkości dv/dr i powierzchni stykających się warstw 2πlr, czyli:

,

gdzie η - współczynnik lepkości danej cieczy. Ciecze stosujące się do tego prawa nazywamy cieczami newtonowskimi.

Współczynnik lepkości jest liczbowo równy wartości siły stycznej, która przyłożona do jednostkowej powierzchni przesuwanej warstwy utrzymuje w tej warstwie przepływ laminarny ze stałym jednostkowym gradientem prędkości warstw.

,

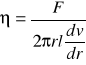
współczynnik ten nosi nazwę lepkości dynamicznej.

Siła F jest równoważona siłą spadku ciśnienia Δp, działającego na powierzchnię przekroju poprzecznego cylindra πr², zatem:

,

skąd po przekształceniu i scałkowaniu w granicach od r do r₀ otrzymamy związek wyrażający zależność prędkości v cieczy od promienia cylindra:

.

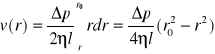
Jak wynika z powyższej zależności ciecz płynąca przez rurę ma paraboliczny rozkład prędkości wzdłuż promienia rury.

Oznaczmy przez Q(r) masę płynu o gęstości ρ, przepływającą w jednostce czasu przez cylinder o promieniu r. Różniczka tej wielkości wyraża się wzorem:

,

gdzie dS=2πrdr - powierzchnia pierścienia o promieniu r i szerokości dr.

Po podstawieniu otrzymamy:

,

po scałkowaniu:

.

Całkowita masa płynu przepływającego przez rurę o promieniu wewnętrznym r₀ i długości l wynosi:

,

gdzie ν=η/ρ - nosi nazwę współczynnika lepkości kinematycznej.

Zależność ta nosi nazwę wzoru Poiseuille'a. Wynika z niej, że ilość wypływającej cieczy jest proporcjonalna do czwartej potęgi promienia otworu. Przytoczone tu rozważania odnoszą się do przewodów o bardzo małej średnicy, noszących nazwę kapilar.

W cieczach newtonowskich w temperaturach znacznie niższych od temperatury krytycznej, zgodnie z teorią dziurową, cząsteczki drgają wokół chwilowych położeń równowagi. Czas przebywania w `dziurze' charakteryzuje średni czas relaksacji, zależny od temperatury. Po otrzymaniu dodatkowej energii cząsteczka może przeskoczyć do nowej dziury. Minimalna energia potrzebna do takiego przeskoku nazywa się energią aktywacji przepływu lepkiego. Taką energią cząsteczka może otrzymać wskutek zderzeń z sąsiednimi cząsteczkami lub też na skutek działania siły zewnętrznej. Współczynnik lepkości cieczy newtonowskich maleje wraz ze wzrostem temperatury zgodnie ze wzorem:

,

gdzie W - energia aktywacji, k -stała Bolzmana. Wielkość A słabo zależy od temperatury i w tym przypadku możemy uznać ją za stałą.

Oprócz lepkości dynamicznej i kinetycznej ciecze i gazy wykazują tzw. lepkość objętościową związaną z rozpraszaniem energii przy dużej częstości procesów nierównowagowych (przy propagacji fal ultradźwiękowych).

Współczynnik lepkości mierzy się tzw. wiskozymetrem. Najczęściej stosuje się wiskozymetry wykorzystujące następujące zjawiska:

- ruchu jednostajnego ciał stałych w płynie lepkim (wiskozymetr Stokesa, Hoepplera),

- przepływu płynu przez rurki kapilarne (wiskozymetry Oswalda, Ubbelohde'a, Englera),

- tłumienie drgań okresowych lub zmniejszanie prędkości ruchów aperiodycznych (rewiskozymetry).

POMIARY

POMIAR NR	TEMPERATURA (°C)	CZAS (MIN:SEK:SSEK)
1	23	2:53:75
2	23	2:23:15
3	43	2:04:59
4	53	1:49:94
5	63	1:40:41
6	73	1:37:72
7	83	Pojawiły się pęcherzyki powietrza

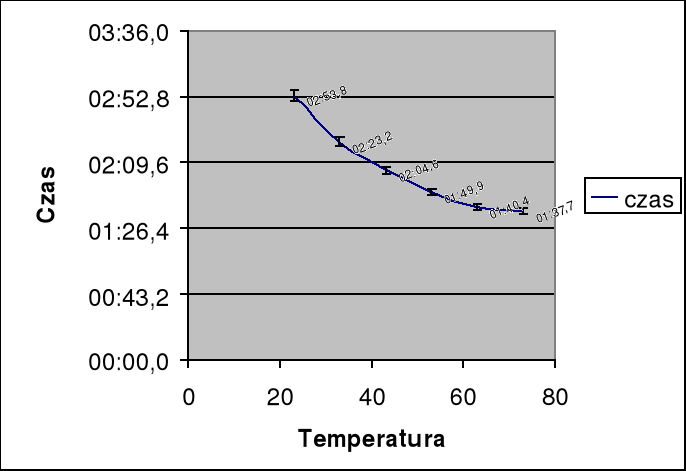
WYKRES

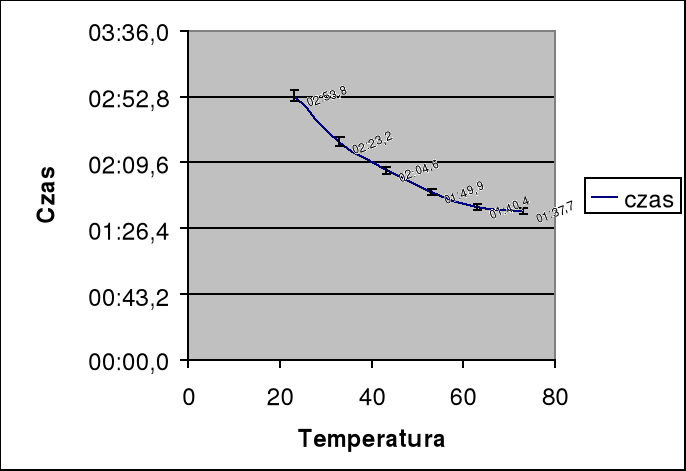
Na załączonym wykresie przedstawiono zależność szubkości wypływu cieczy od temperatury.

WNIOSKI

Obserwując przebieg wykresu zależności czasu wypływu wody od jej temperatury, zauważamy, że zależność ta, a więc również lepkość, maleje wraz ze wzrostem temperatury. Wykres potwierdza to, że zależność lepkości wody od temperatury jest funkcją ekspotencjalną
.

---