Ćwiczenie nr: 1
Rok: I	semestr: letni	Wyznaczanie momentu bezwładności ciał metodą wahadła fizycznego grawitacyjnego i sprawdzanie twierdzenia Steinera.
Wydział Elektroniki i Telekomunikacji Politechniki Wrocławskiej					Ocena:
5.04.2000 r.

1. Wstęp teoretyczny.

Ruchem drgającym nazywamy każdy ruch lub zmianę stanu, które charakteryzuje powtarzalność w czasie wartości wielkości fizycznych, określających ten ruch lub stan. Jeżeli wartości wielkości fizycznych zmieniające się podczas drgań powtarzają się w równych odstępach czasu to ruch taki nazywamy ruchem okresowym.

Najprostszy rodzaj drgań okresowych są drgania harmoniczne.

Okresem drgań harmonicznych nazywamy najmniejszy odstęp czasu, po upływie którego powtarzają się wartości wszystkich wielkości fizycznych charakteryzujących drganie.

Jako przykład drgań harmonicznych można podać niewielkie wahania wahadła fizycznego.

Wahadło fizyczne jest to ciało doskonale sztywne, które pod wpływem własnego ciężaru waha się dookoła osi nie przechodzącej przez środek ciężkości ciała.

Okres drgań harmonicznych [T] wahadła fizycznego można wyznaczyć korzystając ze wzoru:

.

Okres drgań harmonicznych nie zależy od kąta wychylenia α z położenia równowagi (izochronizm wahań).

Twierdzenie Steinera.

Po przekształceniu wzoru na okres drgań (w/w) otrzymujemy następujące wyrażenie na moment bezwładności:

.

Moment ten jest mierzony względem osi obrotu wahadła.

W praktyce często przydatna jest znajomość momentów bezwładności mierzonych względem osi przechodzącej przez środki ciężkości tych ciał.

Do wyznaczenia momentu bezwładności ciała
względem osi przechodzącej przez środek masy ciała korzysta się z twierdzenia Steinera, które brzmi następująco: różnica momentów bezwładności ciała względem dwu równoległych osi, z których jedna przechodzi przez środek masy, równa jest iloczynowi masy ciała m i kwadratu odległości d między osiami:

.

Dla dwu różnych odległości
i
od osi przechodzącej przez środek masy ciała mamy:

.

Po podstawieniu poprzedniego wzoru otrzymujemy:

.

Otrzymana doświadczalnie stała wartość powyższych wyrażeń może służyć jako potwierdzenie twierdzenia Steinera.

Stała C pozwala obliczyć moment bezwładności ciała względem osi przechodzącej przez środek masy:

.

2. Cel ćwiczenia:

1. Stwierdzenie zależności okresu drgań wahadła od momentu bezwładności.

2. Doświadczalne potwierdzenie twierdzenia Steinera.

3. Wyznaczenie momentu bezwładności ciał względem osi przechodzącej przez środek masy (tzw. osi środkowej).

3. Urządzenie pomiarowe.

• tarcza metalowa z symetrycznie naciętymi otworami, które pozwalały zmieniać odległości osi obrotu od środka masy tarczy;

• pierścień metalowy, dla którego daje się zrealizować tylko jedno położenie osi obrotu względem środka masy;

• suwmiarka do pomiaru odległości osi obrotu;

• elektroniczny licznik okresów;

• waga laboratoryjna do wyznaczenia masy tarczy i pierścienia.

4. Przebieg ćwiczenia:

1. Pomiary tarczy z otworami.

4.1.1.

a) 2d = 149mm ±0,1mm

d = 74,5mm = 0,0745m ±0,0001m

POMIAR	100T [s]	Δ 100T	C [ ]	ΔC [ ]
1.	69,615	0,031
2.	69,615	0,031
3.	69,755	0,109
4.	69,601	0,045
średnia	69,646	0,054	0,135	0,0007

T₁ = 0,69646 s ± 0,00054 s

b) 2d = 98 mm ± 0,1 mm

d = 49 mm = 0,049 m ± 0,0001 m

POMIAR	100 T [s]	Δ 100 T [s]	C [ ]	ΔC [ ]
1.	68,577	0,306
2.	69,024	0,141
3.	69,033	0,150
4.	68,897	0,014
średnia	68,883	0,153	0,133	0,0011

T₂ = 0,68883 s ± 0,00153 s

c) 2d = 48 mm ± 0,1 mm

d = 24 mm = 0,024 m ± 0,0001 m

POMIAR	100 T [s]	Δ 100 T [s]	C [ ]	ΔC [ ]
1.	70,448	0,938
2.	69,987	0,477
3.	69,276	0,234
4.	68,329	1,181
średnia	69,510	0,707	0,091	0,0025

T₃ = 0,6951 s ± 0,00707 s

1. Wyznaczenie średniej wartości C :

m = 1061,3 g ± 1 g = 1,0613 kg ± 0,001 kg

POMIAR	C [m^2]	ΔC [m^2]
1.	0,135	0,0007
2.	0,133	0,0011
3.	0,091	0,0025
Średnia	0,1197	0,00143

Przykładowe obliczenia:

• wyznaczanie stałej C:

• błąd stałej C obliczamy z różniczki zupełnej:

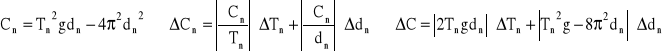
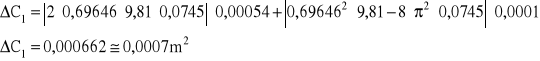
Korzystając ze wzoru
obliczamy moment bezwładności
względem środka masy krążka otrzymałem:

m = 1,0613 kg

Δm = 1g = 0,001 kg

• błąd bezwzględny wyznaczamy za pomocą pochodnej logarytmicznej:

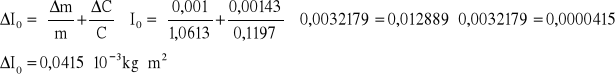
1. Pomiaru pierścienia metalowego.

4.2.1.

2d = 105 mm ± 0,1mm

d = 52,5 mm = 0,0525 m ± 0,0001m

POMIAR	100 T [s]	Δ 100 T [s]
1.	67,620	0,409
2.	66,549	0,662
3.	67,252	0,041
4.	67,425	0,214
Średnia	67,211	0,331

T = 0,67211 s ± 0,00331 s

• masa pierścienia.

m = 220,3 g = 0,2203kg

Δm = 1g = 0,001kg

a) Moment bezwładności pierścienia I wyliczamy ze wzoru:

• błąd wyznaczamy za pomocą pochodnej logarytmicznej:

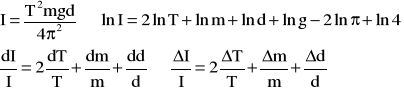
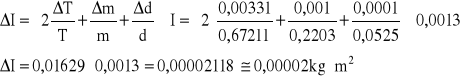
b) Obliczanie momentu bezwładności względem środka masy (z twierdzenia Steinera):

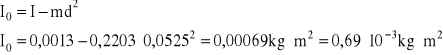
• błąd wyznaczamy za pomocą różniczki zupełnej:

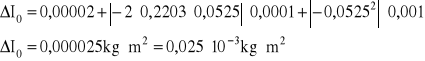
c) Obliczenie momentu bezwładności pierścienia względem środka masy ze wzoru tablicowego:

gdzie:

r - promień wewnętrzny : 0,0525m,

R - promień zewnętrzny : 0,06m.

• błąd wyznaczamy za pomocą różniczki zupełnej:

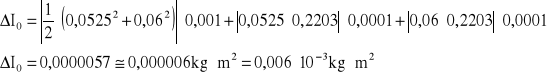
4.2.2. Porównanie wyników obliczeń
dla pierścienia metalowego:

METODA	I0 10^-3[kg∙m^2]	ΔI0 10^-3[kg∙m^2]
Z twierdz. Steinera	0,69	0,03
Ze wzoru tablicowego	0, 7	0,006

5. Wnioski.

Potwierdzeniem założenia Steinera, jest stała C, która została obliczona dla różnych odległości od osi przechodzącej przez środek masy ciała. Stała ta (dla każdego d i odpowiadającego mu T) posłużyła mam między innymi do wyliczenia momentu bezwładności ciała względem osi przechodzącej przez środek masy. W naszych pomiarach teoria ta potwierdziła się ( z niewielkimi odstępstwami zniwelowanymi rachunkiem błędów), co umożliwiło otrzymanie bardzo dokładnej wartości momentu bezwładności tarczy metalowej, względem osi przechodzącej przez środek ciężkości.

Dla kolejnych pomiarów stałej C na dokładność pomiarów miały wpływ takie czynniki jak:

• Pomiar odległości d środka obrotu od środka masy krążka metalowego (niedokładność związana z ustawieniem suwmiarki i odczytem jej podziałki). Pomiary te były pomiarami pojedynczymi z przyjętym błędem narzędzia pomiarowego

• Pomiar okresu drgań, na który miał wpływ moment zatrzymania licznika elektronicznego, a także precyzja odczytu jego wskazań. Pomiar okresu dla zwiększenia dokładności był wykonany dla stu okresów, a oprócz tego wykonany został kilka razy. Taka ilość wyników pomiaru pozwoliła oszacować średni okres wraz z błędem.

• Na stałą C wpływało także tarcie na styku wahadła i belki, na której było ono zawieszone (przekrój belki był trójkątny, lecz jego wierzchołek był nieco zaokrąglony). Staraliśmy się unikać poślizgów tarczy i pierścienia oraz odbić od pryzmy, wychylając wahadło o tak mały kąt α , przy którym równanie ruchu ( sin α ) zachowuje liniowość.

Błędy wyników złożonych obliczyłem metodą różniczki zupełnej lub pochodnej logarytmicznej, na które istotny wpływ miały zaokrąglenia wartości π oraz stałej g.

W drugiej części ćwiczenia zajęliśmy się sprawdzaniem prawa Steinera. Wyznaczenie momentu bezwładności pierścienia wzg. osi oddalonej o odległość d od środka ciężkości dało ( zgodnie ze sprawdzanym prawem) możliwość wyznaczenia I₀.

Dla pierścienia metalowego na pomiar I₀ wpływały te same czynniki, które wpływały na dokładność pomiaru momentu bezwładności metalowej tarczy.

Dla metalowego pierścienia:

Korzystając z twierdzenia Steinera otrzymałem I₀=0, 68∙10^-3 kg m².

Po obliczeniu Io ze wzoru tablicowego otrzymałem I₀=0, 7∙10^-3 kg m².

Po porównaniu obu wyników otrzymałem różnice, która wynosi 0,02∙10^-3 kg m².

Okazuje się, ze dokładniejszy było wyliczenie Io ze wzoru tablicowego. Wynik ten jednak zawiera się w przedziale błędu wyniku otrzymanego z twierdzenia Steinera, czym udowodniliśmy słuszność jego praw.

---