• Laboratorium fizyki CMF PŁ

• Dzień ............ godzina................ grupa..........

Wydział _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

semestr _ _ _ _ _ _ _ _ _ _ rok akademicki _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

ocena _____

1. Cel ćwiczenia:

Celem ćwiczenia było zbadanie prędkości światła za pomocą zmian faz promienia świetlnego.

2. Zdjęcie układu pomiarowego:

3. Schemat układu do pomiaru prędkości światła w powietrzu oraz elementów przyrządu pomiarowego.

4. Schemat blokowy oscyloskopu

5.Schemat lampy oscyloskopowej.

1. Grzejnik

2. Katoda

3. Cylinder Wehnelta

4. Anoda pierwsza

5. Anoda druga

6. Płytki odchylania pionowego

7. Płytki odchylania poziomego

8. Ekran

6. Schemat pokazujący odległości wyznaczone przy pomiarze współczynnika załamania w ciele stałym lub w cieczy.

7. Tabelka pomiarowa: Pomiar prędkości światła w powietrzu.

Przy obliczaniu prędkości światła korzystaliśmy z następującego wzoru:

gdzie:

f - częstotliwość modulacji

Δx - odległość zwierciadła od źródła światła

Nr. pomiaru	Odległość Δx [cm]	Częstotliwość f [MHz]	Prędkość światła c [m/s]
1	150	50.1	300600000
2	151	50.1	302604000
3	151	50.1	302604000
4	149	50.1	298596000
5	149	50.1	298596000
6	150.5	50.1	301602000
7	151	50.1	302604000
8	149.5	50.1	299598000
9	149.6	50.1	299798400
10	149.5	50.1	299598000
Średnia	150	50.1	300600000

Przykładowe obliczenie prędkości:

8. Wyznaczenie współczynnika załamania światła

8.1. Dla rurki z wodą o długości 101,9cm

Przy obliczaniu współczynnika załamania wody korzystaliśmy z następującego wzoru:

Nr. pomiaru	Odległość z rurą x1 [cm]	Odległość bez rury x2 [cm]	Współczynnik załamania n
1	100	118	1.35
2	100.5	117.5	1.33
3	100.25	117.6	1.34
4	101	117.6	1.32
5	100.5	117.8	1.34
6	100	118	1.35
7	100.25	118	1.35
8	100.5	117.9	1.34
9	100.25	117.6	1.34
10	100.9	118	1.34
Średnia	100.41	117.8	1.34

Przykładowe obliczenie współczynnika załamania:

8.2. Dla klocka żywicznego o długości 28.5cm

Przy obliczaniu współczynnika załamania wody korzystaliśmy z następującego wzoru:

Nr. pomiaru	Odległość z klockiem x1 [cm]	Odległość bez klocka x2 [cm]	Współczynnik załamania n
1	40	47	1.49
2	39.8	46.5	1.47
3	40	46.6	1.46
4	39.6	47	1.52
5	40	46.9	1.48
6	39.9	46.5	1.46
7	39.8	46.6	1.48
8	39.9	46.8	1.48
9	39.8	46.7	1.48
10	39.7	46.8	1.50
Średnia	39.85	46.74	1.48

Przykładowe obliczenie współczynnika załamania:

8.3. Dla klocka żywicznego o długości 16.5cm

Przy obliczaniu współczynnika załamania wody korzystaliśmy z następującego wzoru:

Nr. pomiaru	Odległość z klockiem x1 [cm]	Odległość bez klocka x2 [cm]	Współczynnik załamania n
1	50	53.5	1.42
2	50.2	53.5	1.40
3	50	54	1.48
4	50.1	53.8	1.45
5	50	53.9	1.47
6	50.2	54	1.46
7	50.1	53.8	1.45
8	50	53.8	1.46
9	50.1	54	1.47
10	50.1	53.9	1.46
Średnia	50.08	53.82	1.45

Przykładowe obliczenie współczynnika załamania:

9. Wnioski i spostrzeżenia

Fale elektromagnetyczne to wzajemnie przenikające się drgania elektryczne i magnetyczne. Fala taka powstaje np. wtedy, gdy elektron w atomie traci energię i przeskakuje na orbitę bliżej jądra atomu. Powstają przy tym drgania elektryczne, które rozchodzą się w przestrzeni w postaci pola elektrycznego i magnetycznego. Pola te są prostopadłe do siebie i do kierunku rozchodzenia się fali.

Długość fali elektromagnetycznej można wyznaczyć korzystając z wzoru:

gdzie:

λ - długość fali [m]

V - prędkość fali

f - częstotliwość drgań żródła [Hz]

Fale elektromagnetyczne ze względu na długość dzielą się na:

Promieniowanie widzialne zawiera się w zakresie od 380 [nm] do 780 [nm].

Światło białe jest mieszaniną wszystkich barw.

Prędkość światła:

Już od początku 17 wieku próbowano wyznaczyć prędkość światła.

Jako pierwszy w 1600r. Próbował zrobić to Galileusz. Wraz ze swoim pomocnikiem stanęli w nocy w 2 latarniach i na zmianę odsłaniali swoje latarki. Galileusz próbował zmierzyć czas przejścia światła tam i z powrotem. Lecz próba ta nie powiodła się gdyż czas reakcji człowieka jest dużo dłuższy niż prędkość rozchodzenia się fali świetlnej.

Następnie jeszcze wiele razy próbowano zmierzyć prędkość światła.

W roku 1856 szkocki fizyk James Clerk Maxwell sformułował równania przez które pokazał wzór na prędkość fali świetlnej w próżni:

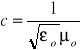
gdzie:

- przenikalność dielektryczna próżni

- przenikalność magnetyczna próżni

Po zatwierdzeniu przez Generalną Konferencję Miar i Wag w 1983r. Definicji metra, jako drogi jaką pokonuje światło w próżni w czasie 1/299 792 458 s, prędkość światła w próżni stała się wzorcem i wynosi dokładnie 299 792 458 m/s.

W naszym ćwiczeniu do wyznaczenia prędkości światła posłużyliśmy się oscyloskopem który porównywał dwa sygnały sinusoidalne o tej samej częstotliwości, lecz różnym przesunięciu fazowym.

Oscyloskop jest uniwersalnym przyrządem pomiarowym służącym do obserwacji przebiegów elektrycznych i pomiaru ich parametrów. Najważniejszą częścią oscyloskopu jest lampa oscyloskopowa, której schemat przedstawiłem w punkcie 6. Jest to szklana bańka z której wyciągnięto powietrze. Wyrzutnia elektronowa znajduje się w tylnej, zwężonej części bańki i składa się z szeregu elektrod, które tworzą układ soczewek elektrycznych skupiających i przyspieszających strumień elektronów. Źródłem elektronów jest pośrednio żarzona cylindryczna katoda tlenkowa o prawie punktowej powierzchni emitującej. W wyniku termoemisji uwolnione elektrony przepływają przez elektrodę przesłonową zwaną cylindrem Wehnelta (S1), która zasilana jest napięciem ujemnym względem katody. Przez zmianę tego napięcia za pomocą rezystora R1 można zmienić natężenie wiązki elektronów, a przez to jasność świecenia plamki. Zadaniem pierwszej anody jest skupienie wiązki elektronów. Zmiana potencjału tej anody za pomocą rezystora R2 powoduje zmianę ostrości plamki świetlnej. Druga anoda przyśpiesz wiązkę elektronów i współdziała z pierwszą anodą przy skupianiu wiązki elektronów. W lampach oscyloskopowych najczęściej stosowany jest układ odchylania elektrostatycznego. Umożliwia on uzyskanie wysokiej częstotliwości pracy lampy. Układ tworzą dwie prostopadłe pary płytek odchylających. Pod wpływem zmian napięcia mierzonego, które najczęściej doprowadzane jest do płytek odchylania pionowego Y, pomiędzy płytkami wytwarzane jest zmieniające się pole elektryczne. Powoduje ono zmianę trajektorii  poruszających się elektronów. Analogiczny proces zachodzi pomiędzy płytkami odchylania poziomego X, które zasilane są napięciem z generatora podstawy czasu. Jeżeli do jednej pary płytek przyłożymy stałą różnicę potencjałów to pole elektrostatyczne odchyli wiązkę elektronów w kierunku elektrody o wyższym potencjale. Jeżeli przyłożymy zmienną w czasie różnicę potencjałów to elektrony będą wykonywały drgania pomiędzy tymi elektrodami. Przy dostatecznie dużej częstotliwości zmian napięcia, będziemy obserwować na oscyloskopie jasną kreskę jako ślad drogi, po której wędruje strumień elektronów. W celu obserwacji przebiegu napięć do płytek odchylania poziomego należy przyłożyć napięcie o piłokształtnym przebiegu.

Napięcie to najpierw powoli rośnie poczym gwałtownie opada. Powoduje to powolny ruch plamki świetlnej z lewej na prawą stronę ekranu, po czym jej gwałtowny powrót. Jeżeli teraz do płytek odchylania pionowego przyłoży się napięcie o nieznanym przebiegu to zostanie ono odwzorowane na ekranie przez ruchomą wiązkę elektronów. Jeśli natomiast zamiast przebiegu piłokształtnego do płytek odchylani poziomego przyłożymy napięcie sinusoidalne o danej częstotliwości, a do płytek odchylania pionowego również przyłożymy napięcie sinusoidalne o częstotliwości takiej samej, lub będącej jej krotnością to na ekranie oscyloskopu zobaczymy figury Lissajous.

Przykład figur Lissajous:

Dokonując pomiaru prędkości porównywaliśmy dwa sygnały o częstotliwości 50.1 MHz, zredukowanej następnie do 50 KHz. Jeden z sygnałów pobraliśmy wprost z mixera, a drugi również z niego lecz sygnał ten miał inny kąt fazowy (rysunek z punktu 4). Zmiana kąta była spowodowana przebyciem dłuższej drogi przez promień świetlny. Na początku ustawiamy lustra odbijające promień świetlny tak aby jego droga była jak najkrótsza, następnie dostrajamy przesunięcie fazowe sygnałów aby było równe
(skośna pojedyncza linia na ekranie oscyloskopu). Następnie odsuwamy lustra na taką odległość aby ponownie linie się pokryły, lecz tym razem pod innym kątem. Kąt przesunięcia sygnałów będzie równy
. Mierząc teraz odległość luster od źródła mamy teraz drogę jaką przebyło światło Δx. Prędkość światła obliczmy dzieląc drogę przez czas w jakim światło ją przebyło
. Zmiana fazy o
mówi nam, że światło potrzebuje na przebycie tej drogi czas równy połowie okresu modulacji sygnału, a więc
, czyli prędkość światła można obliczyć korzystając ze wzoru:
, gdzie f jest częstotliwością modulacji równą f=50.1 MHz. Wyznaczając średnią naszych pomiarów wyznaczyliśmy prędkość światła która wyniosła 300600000
. Rzeczywista prędkość światła wynosi 299792458
. Błąd względny pomiaru można obliczyć korzystając ze wzoru
. Gdzie:

-Wartość rzeczywista prędkości światła

- Wartość obliczona prędkości światła

Podstawiając wartości do wzoru otrzymujemy: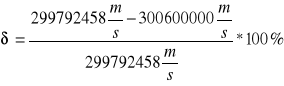
. Błąd ten wynosi: δ= -0.27%. Spowodowany on jest głównie niedokładnością przy odczycie z oscyloskopu linii(czy już się pokrywają, czy nie), oraz niedokładnością odczytu podziałki położenia luster.

Kolejnymi pomiarami jakie dokonywaliśmy był pomiar współczynnika załamania światła dla wody oraz klocka żywicznego (schemat punkt 6).

Wyznaczenie tych współczynników poległo jedynie na porównaniu prędkości światła w powietrzu do prędkości światła w wyżej wymienionych ośrodkach.
, gdzie:

c - prędkość światła w powietrzu

c_{m -} prędkość światła w badanym ośrodku

Czas przebiegu światła w powietrzu można obliczyć korzystając ze wzoru :
,

Natomiast czas przejścia światła przez badane ośrodki możemy wyznaczyć ze wzoru:
. Porównując te czasy otrzymujemy wzór na współczynnik załamania:
. Z naszych pomiarów wynika, że współczynnik załamania światła w wodzie jest mniejszy od współczynnika załamania światła w klocku żywicznym i wynosi 1.34. Fakt ten wynika z tego, że woda ma mniejszą gęstość niż klocek żywiczny.

Pomiary współczynnika załamania z klockiem żywicznym wykonaliśmy dwukrotnie:

Raz przy długości 28.5 cm, a drugi raz przy długości 16.5 cm. Większy współczynnik załamania światła otrzymaliśmy przy pomiarze klocka o długości 28.5 cm. Wynika z tego, że światło przebywszy dłuższą drogę przez dany ośrodek ulega większemu załamaniu.

Wnioski wynikające z powyższych rozważań są następujące:

• prędkość światła można obliczyć porównując przesunięcie fazowe 2 sygnałów o jednakowej częstotliwości wychodzących z jednego źródła

• Współczynnik załamania światła zależy od rodzaju ośrodka przez który ono biegnie

• Współczynnik załamania zależy również od długości tego ośrodka

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

imię i nazwisko

nr indeksu

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

imię i nazwisko

nr indeksu

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

imię i nazwisko

nr indeksu

Kod ćwiczenia	Tytuł ćwiczenia
W1	Pomiar prędkości światła

---