Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z pojęciem charakterystyki częstotliwościowej, praktycznym sposobem jej rejestracji oraz wykorzystania do identyfikacji własności dynamicznych badanego elementu.

Przebieg ćwiczenia:

1. Zarejestrować charakterystykę amplitudowo-fazową zadanego czwórnika.

2. Narysować charakterystyki logarytmiczne badanego czwórnika.

3. Przeprowadzić identyfikację badanego czwórnika.

Wiadomości ogólne:

Charakterystyki częstotliwościowe zawierają pełną informacje o dynamice

układów regulacji. Charakterystyki te zarówno w teorii jak i w praktyce zajmują ważne miejsce w układach automatycznego sterowania. Określone są one w zasadzie dla układów liniowych choć i dla układów zlinearyzowanych także mogą być stosowane (jednak tylko dla pewnych klas). Zasadą wyznaczania charakterystyk częstotliwościowych jest na wejściu badanego układu podawanie wymuszenie harmoniczne : x(t)=xsint. Jeżeli badany układ jest liniowy i nie działają na niego żadne dodatkowe wymuszenia i zakłócenia , wówczas na wyjściu układu w stanie ustalonym pojawia się sygnał wyjściowy y(t)=y₀sin (ωt+φ). Układ pomiarowy jest przyrządem specjalistycznym. Składa się on z generatora przebiegów harmonicznych oraz mierników wzmocnienia k = y₀(ω)/x₀(ω). Generator bezpośrednio połączony jest z miernikiem w celu uzyskania sygnału odniesienia x(t) dla pomiaru wzmocnienia k(ω) i przesunięcia fazowego φ(ω) do miernika podłączony jest jednocześnie sygnał wyjściowy y(t) z badanego układu. Podstawą teoretyczną jest transmitancja widmowa y(jω)=G(s) (s=jω). Pomiędzy charakterystyką rzeczywistą i urojoną a charakterystykami amplitudową M(ω) i fazową φ(ω) istnieją zależności:

,
,

Korzystając z równań można wyznaczyć analitycznie poszczególne charakterystyki:

1 .Częstotliwościowa urojona:

2.Częstotliwość rzeczywista:

3.Częstotliwość amplitudowa:

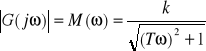
4.Częstotliwość fazowa :

Transmitancję widmową można zapisać :

Charakterystyki amplitudowa i fazowa są przedstawiane we współrzędnych logarytmicznych:

- logarytmiczna charakterystyka amplitudowa ;

-logarytmiczna charakterystyka fazowa.

Zadanie sprowadza się głównie do identyfikacji obiektu czyli uzyskania wiarygodnego opisu matematycznego w postaci równań różniczkowych o stałych współczynnikach lub transmitancji operatorowej albo charakterystyki częstotliwościowej, amplitudowej i fazowej. Pierwsza metoda prowadząca do bezpośredniego wyznaczenia równania różniczkowego układu , polega na identyfikacji układu na podstawie przebiegów czasowych.

Drugą dokładniejszą metodą jest identyfikacja układu na podstawie metod częstotliwościowych.

Charakterystykę amplitudowo - fazową można zdefiniować jako wykres na płaszczyźnie zespolonej modułu

M(ω) i argumentu φ(ω) transmitancji widmowej G(jω) w funkcji pulsacji ω.

Rys. Wykres charakterystyki częstotliwościowej ampliludowo-

fazowej na płaszczyźnie zespolonej z oznaczeniem

składowych wektora G(jω) dla obiektu o transmitancji

widmowej G(jω) = k/(jωT + 1)

Zasada wyznaczania charakterystyk częstotliwościowych:

Na wejście badanego obiektu, układu lub elementu podawane jest wymuszenie harmoniczne o postaci:

Jeżeli badany obiekt jest liniowy i nie działają na niego żadne dodatkowe wymuszenia i zakłócenia, wówczas na wyjściu obiektu w stanie ustalonym pojawia się sygnał wyjściowy y(t) opisany zależnością:

Wprost z przebiegów czasowych, które można otrzymać z wejścia i wyjścia badanego obiektu, zapisując je za pomocą rejestratora wielokanałowego, można określić następujące parametry przebiegów:

Rejestrator musi spełniać następujący warunek: w paśmie pulsacji badania obiektu od ω_min do ω_max nie może wynosić przesunięcia fazowego φ_r, ponadto musi być znane wzmocnienie kanałów rejestratora, co pozwala wprost z przebiegów czasowych x(t) i y(t), wyznaczyć x₀ i y₀.

Rys. Schemat blokowy układu pomiarowego do zdejmowania charakterystyk częstotliwościowych elementów elektrycznych

Wyniki pomiarów i obliczenia:

ω	P(ω)	Q(ω)	M(ω)	L(ω)	φ(ω)
[Hz]	[mV]	[mV]	[mV]	[dB]
3	72	-8,4	72,49	37,2	-6,65
5	70,7	-13,0	71,88	37,1	-10,42
15	58,3	-29,9	65,52	36,32	-27,15
25	43,2	-36,4	56,49	35,04	-40,12
30	35,3	-37,1	51,21	34,18	-46,42
35	29,9	-36,5	47,18	33,47	-50,67
45	21,8	-34,2	40,55	32,16	-57,48
55	16,3	-31,2	35,20	30,93	-62,41
65	12,5	-28,4	31,03	29,83	-66,24
75	9,9	-25,3	27,72	28,85	-69,08
85	7,9	-23,7	24,98	27,94	-71,56
95	6,5	-21,8	22,75	27,14	-73,39
105	5,4	-20,2	20,91	26,40	-75,03
115	4,6	-18,8	19,35	25,73	-76,25
125	3,9	-17,6	18,03	25,12	-77,50
145	3,0	-15,6	15,89	24,02	-79,11
165	2,3	-14,1	14,27	23,39	-80,73
185	1,8	-12,8	12,92	22,22	-81,99
205	1,5	-11,7	11,79	21,43	-82,69
245	1,0	-10,2	10,25	20,21	-84,40
285	0,7	-9,0	9,02	19,10	-85,55
345	0,5	-7,7	7,71	17,74	-86,28
395	0,4	-7,0	7,01	16,91	-86,73
445	0,2	-6,4	6,40	16,13	-88,21
545	0,1	-5,5	5,50	14,80	-88,96

Podczas ćwiczeń z przyrządów pomiarowych zostały odczytane następujące wartości wartości :

> Pulsacja ω

> Wartość rzeczywista P(ω)

> Wartość urojona Q(ω)

Pozostałe wartości zostały obliczone według następujących wzorów:

Moduł transmitancj i widmowej:

Logarytmiczna charakterystyka amplitudowa:

Logarytmiczna charakterystyka fazowa:
:

Wnioski

Z przeprowadzonych pomiarów na podstawie charakterystyk częstotliwościowych poprzez porównanie eksperymentalnie wyznaczonych wykresów z wykresem wzorcowym wynika, że badany czwórnik elektryczny był elementem inercyjnym pierwszego rzędu. Przesunięcia niektórych punktów charakterystyk wynikają z niedokładności przeprowadzonych pomiarów.

6

---