OZNACZENIA:

R(t) − funkcja niezawodności,

F(t) − funkcja zawodności,

ET − oczekiwany czas zdatności,

f(t) − gęstość prawdopodobieństwa uszkodzenia,

λ − intensywność uszkodzeń,

Struktury niezawodnościowe:

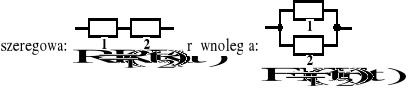
Wzory ogólne:

R(t) + F(t) = 1 ,
,

Rozkład wykładniczy czasu zdatności:

Dla elementu:
,
,
,

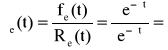
− dla rozkładu wykładniczego intensywność uszkodzeń elementu jest stała,

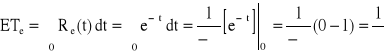
− oczekiwany czas zdatności elementu,

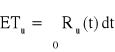
− oczekiwany czas zdatności urządzenia,

Rozkład jednostajny czasu zdatności:

Dla elementu:
,
,
,

−

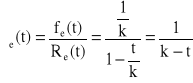
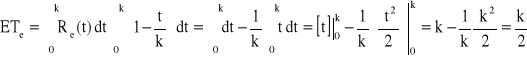
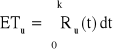
− oczekiwany czas zdatności urządzenia,

Używane całki i pochodne:

,
,
,
Intensywność uszkodzeń − λ(t) − jest to warunkowe prawdopodobieństwo tego, że obiekt uszkodzi się

w przedziale czasu (t, t + Δt] pod warunkiem, że do chwili t pracował poprawnie, podzielone przez Δt.

Gęstość prawdopodobieństwa uszkodzenia − f(t) − określa prawdopodobieństwo, z jakim uszkodzi się obiekt w danej chwili t.

Miary niezawodności obiektu:

− oczekiwany czas zdatności (średni czas pracy do uszkodzenia),

− intensywność uszkodzeń (ilość uszkodzeń w jednostce czasu),

− prawdopodobieństwo, że obiekt się nie uszkodzi do pewnej chwili t,

− prawdopodobieństwo, że obiekt jest zdolny do działania w pewnej chwili t.

Ilościowe miary niezawodności obiektu nienaprawialnego:

− funkcja niezawodności - R(t),

− intensywność uszkodzeń - λ(t),

− oczekiwany czas zdatności - ET.

Ilościowe miary niezawodności obiektu naprawialnego:

− funkcja gotowości,

− współczynnik gotowości,

− intensywność uszkodzeń,

− intensywność odnowy,

− proces odnowy,

− funkcja odnowy.

Oczekiwany czas zdatności − ET − średni czas pracy obiektu do chwili uszkodzenia,

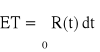
− czyli pole pod krzywą funkcji niezawodności

Pozostały oczekiwany czas zdatności − E(t) − warunkowa wartość oczekiwana zmiennej losowej T − t (pozostały czas zdatności), pod warunkiem, że do chwili t obiekt był zdatny −
.

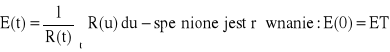
Proces odnowy − N(t) − jest to punktowy proces losowy przedstawiający ilość uszkodzeń, która wystąpiła do chwili t.

Funkcja odnowy − H(t) − jest wartością oczekiwaną procesu odnowy, tj. przeciętną liczbą uszkodzeń danego obiektu, które wystąpią do danej chwili t.

Nadmiar strukturalny − system taki składa się z elementów podstawowych realizujących jego funkcje oraz z elementów rezerwowych włączających się do pracy w razie uszkodzenia się elementów podstawowych.

Nadmiar funkcjonalny − niektóre elementy takiego systemu są wielofunkcyjne. Element wykonuje ściśle określoną funkcję, natomiast w określonych sytuacjach może pełnić dodatkową funkcje elementu uszkodzonego.

Nadmiar czasowy − do współdziałania takiego systemu są wprowadzone określone normatywy czasowe, w których zakresie współdziałanie może być realizowane.

Nadmiar parametryczny − system taki ma duże wymagania zarówno co do niezawodności, jak i bezpieczeństwa. Jest to np. przyjmowanie współczynników bezpieczeństwa w budowie maszyn.

Rezerwa obciążona − element podstawowy i elementy rezerwowe poddawane są tym samym obciążeniom wynikającym z warunków pracy. Własności elementów zmieniają się w taki sam sposób, czyli nie możemy określić, który z elementów jest rezerwowy i który wcześniej ulegnie uszkodzeniu. Czas zdatności urządzenia jest równy: T_u = max(T₁,T₂,... ,T_n).

Rezerwa nieobciążona − element podstawowy pracuje, rezerwowe elementy oczekują na uszkodzenie elementu podstawowego. Czas zdatności urządzenia jest równy sumie czasów zdatności poszczególnych elementów. Spełnione jest równanie: ET_u = ET_o + ET₁ + ET₂ + ... + ET_n.

Rezerwa częściowo obciążona − elementy rezerwowe poddawane są pewnemu obciążeniu w czasie oczekiwania na włączenie (ich własności niezawodnościowe zmieniają się w czasie). Czas zdatności urządzenia jest równy: T_u = T_o + T₁/T_o,T₁ + T₂/ T_o,T₁,T₂ + ...

Funkcja niezawodności − R(t) − prawdopodobieństwo, że obiekt może spełniać wymaganą funkcję w danych warunkach w ustalonym czasie. R(t) = P(T ≥ t), T − zmienna losowa czasu pracy obiektu do powstania uszkodzenia.

Funkcja zawodności − F(t) − prawdopodobieństwo, że obiekt nie będzie spełniać wymaganej funkcji w danych warunkach w ustalonym czasie. F(t) = P(T ≤ t), T − zmienna losowa czasu pracy obiektu do powstania uszkodzenia.

Funkcja gotowości − (jest miarą gotowości obiektu odnawialnego) jest to prawdopodobieństwo tego, że obiekt znajduje się w stanie zdatności w chwili t.

Współczynnik gotowości − jest to wartość graniczna funkcji gotowości przy czasie dążącym do nieskończoności.

oczekiwany czas

zdatności elementu

---