Kadi 3T3

TEMAT:

26. Zbadać algorytm quicksort z losowaniem elementu dzielącego pod względem złożoności czasowej oczekiwanej.

Owocem mojej pracy jest plik test.m testujący badanie podanego algorytmu.

Danymi wejściowymi są wektory długości n zmieniającego się od 2 do 200. Dla każdej długości wektora losowane jest 100 różnych wektorów, zliczana jest ilość odpowiednich operacji i dzielona przez 100, przez co otrzymujemy wynik uśredniony - oczekiwany.

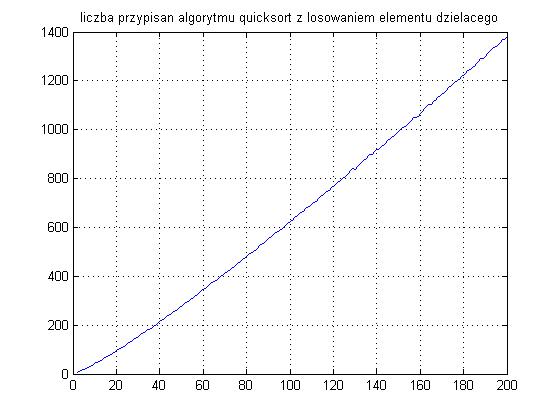
Otrzymane wykresy:

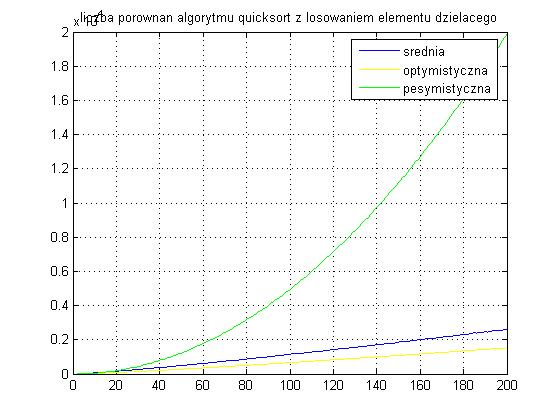
Ja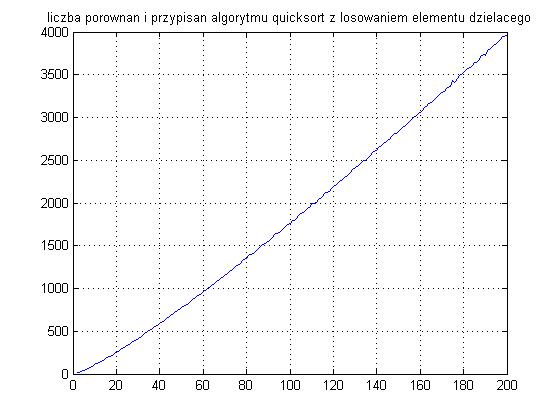
k widać na wykresie drugim, złożoność oczekiwana (gdy liczymy porównania) jest dużo bardziej zbliżona do wartości optymistycznej niż pesymistycznej.

Niestety na wykładzie nie było podanych wzorów na złożoności pesymistyczne i optymistyczne tego algorytmu, a udało mi się jedynie wyznaczyć takie złożoności dla porównań.

Podsumowując można stwierdzić, że algorytm ten jest bardzo wydajny a jego złożoność ma charakterystykę kwadratową tylko dla skrajnie pesymistycznych danych, poza tymi przypadkami algorytm ma złożoność liniowo logarytmiczną (wykres 2, linie żółta i niebieska)