Estymacja parametrów strukturalnych ekonometrycznego modelu liniowego

gdzie

i=0,...,n - parametry strukturalne

Estymacja może być przeprowadzana za pomocą KMNK (Klasycznej metody najmniejszych kwadratów).

Zadanie polega na znalezieniu funkcji liniowej, której wartości
są możliwie bliski wartością
.

Estymatorem nieznanego parametru pewnego rozkładu losowego nazywa się ocenę tego parametru uzyskaną na podstawie danych empirycznych.

- estymator rzeczywistej wartości parametru

Równanie modelu po estymacji parametrów

Do oszacowania parametrów strukturalnych w Excelu wykorzystujemy funkcję RegLinP, natomiast w programie Statistica moduł Regresja wieloraka.

Parametry na które należy zwrócić uwagę podczas procesu estymacji:

- estymatory parametrów

- błąd oceny parametru (o ile średnio statystycznie pomyliliśmy się szacując parametry strukturalne).

Estymatory pochodzące z KMNK gwarantują wymaganą jakość modelu, tzn. są to dobre estymatory charakteryzujące się właściwościami:

• nieobciążalność;

• zgodność;

• efektywność.

Zbudowany model ekonometryczny powinien możliwie wiernie odzwierciedlać wybrany fragment rzeczywistości ekonomicznej. Dlatego, są nakładane trzy warunki na estymatory parametrów strukturalnych modelu.

1. Dopuszczalność - Estymatory parametrów modelu przybierają wartość dopuszczalną ze względów merytorycznych;

2. Koincydencja - zgodność znaku wartości estymatora parametru i znaku współczynnika korelacji odpowiedniej
   

3. Stabilność - dla różnych szeregów realizacji zmiennych wartości estymatora różnią się nieistotnie.

Weryfikacja modelu cd....

1. Badanie dopasowania modelu do danych

2. Badanie statystycznej istotności parametrów strukturalnych modelu

3. Badanie wybranych właściwości reszt modelu

Ad 1. Badanie dopasowania modelu do danych

1. Współczynnik determinacji

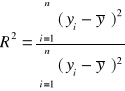
Dopasowanie jest tym lepsze im współczynnik determinacji jest bliższy 1.

2. Współczynnik zgodności (zbieżności) -
   

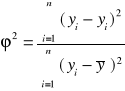
Dopasowanie jest tym lepsze im współczynnik zgodności jest bliższy 0.

Własności:

+
=1

wartości
,
są z zakresu <0-1>.

3. Współczynnik zmienności losowej

Pokazuje jaką część średniej wartości zmiennej objaśnianej (Y) stanowi przeciętne odchylenie wartości teoretycznych od wartości empirycznych zmiennej objaśnianej.

;

gdzie
odchylenie standardowe reszt modelu.

Ad 2. Badanie statystycznej istotności parametrów strukturalnych modelu

Statystyczną istotność parametru
ocenia się na podstawie estymatora
. Na wszystkie testy wykonywane na zajęciach przyjmuje się poziom istotności
=0,05.

Zakłada się dwie hipotezy:

:
- parametr jest nieistotny statystycznie

:
- parametr jest istotny statystycznie

Narzędziem weryfikacji hipotez jest test statystyczny (statystyka testowa) w postaci:

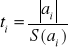
- t-Studenta (n-m)

Przy założeniu prawdziwości
statystyka podlega rozkładowi t-Studenta z parametrem (n-m) stopni swobody.

- wyznaczamy z tablic testu t-Studenta

Wniosek:

Jeżeli
to parametr
jest statystycznie istotny, a zmienna
w istotny sposób wpływa na zmienną Y.

Jeżeli
to parametr
jest statystycznie nieistotny, a zmienna
w istotny sposób wpływa na zmienną Y.

Koincydencja - zgodność znaku wartości estymatora parametru i znaku współczynnika korelacji odpowiedniej
.

Wektor reszt

---