Laboratorium podstaw fizyki

Piotr Suszyński (141141)	Ćwiczenie nr 84 Temat: Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
Grupa: piątek 14:45 - 16:55 Data: 31.03.2006	Prowadzący zajęcia: mgr inż. Andrzej Andruchów	Ocena:

1. Cel ćwiczenia

Celem przeprowadzonego ćwiczenia było:

• wyznaczenie stałej siatki dyfrakcyjnej oraz zapoznanie się ze sposobem jej działania

• wyznaczenie długości fal światła przepuszczanego przez filtry interferencyjne

2. Wstęp teoretyczny

Siatka dyfrakcyjna - jeden z najprostszych przyrządów do przeprowadzania analizy widmowej. Tworzy ją układ równych, równoległych i jednakowo rozmieszczonych szczelin. Jest to przezroczysta lub półprzezroczysta płytka - kryształowa, szklana lub z tworzywa sztucznego. Na jedną ze stron płytki zostaje naniesiona seria równoległych nieprzezroczystych linii, o stałym i odpowiednio małym rozstawie - od kilkunastu linii na milimetr aż do tysiąca w przypadku dobrych siatek. Działanie siatki dyfrakcyjnej polega na wykorzystaniu zjawiska dyfrakcji i interferencji światła do uzyskania jego widma. W tym celu pomiędzy źródłem światła a ekranem umieszcza się siatkę dyfrakcyjną. Na ekranie uzyskuje się w ten sposób widmo światła. Jako pierwszy prymitywną siatkę dyfrakcyjną zastosował angielski fizyk Thomas Young. Przeprowadził on doświadczenie, w którym wiązka światła, przechodząc przez dwie jednakowe, wzajemnie równoległe szczeliny, ugina się na nich i daje po przejściu przez nie dwie spójne, interferujące ze sobą fale. W wyniku interferencji otrzymuje się na ekranie, umieszczonym w znacznej odległości za szczelinami, jasne i ciemne prążki interferencyjne. Siatka dyfrakcyjna jest w zasadzie powieleniem doświadczenia z dwiema szczelinami. Zasadnicza różnica polega na tym, że zamiast dwóch znajduje się na niej duża liczba (od kilkudziesięciu do kilkunastu tysięcy) jednakowych, równoodległych szczelin.

Stałą siatki dyfrakcyjnej, tj. odległość d między jej szczelinami, można obliczyć korzystając z równania siatki dyfrakcyjnej, określającego kierunki interferencyjnego wzmacniania się natężenia światła (maksima):

,

gdzie:

θ_m - kąt ugięcia promieni światła padających na siatkę dyfrakcyjną

m=0, ±1, ±2, ±3... - rząd widma dyfrakcyjnego

λ - długość fali padającej na siatkę

Zakłada się przy tym, że ekran na którym ma miejsce interferencja promieni leży bardzo daleko. W praktyce ugięte promienie przepuszcza się przez obiektyw Ob. Wtedy wszystkie wzajemnie równoległe, ugięte promienie spotykają się i interferują w płaszczyźnie ogniskowej tego obiektywu. Ten sposób realizacji interferencji jest wygodniejszy, a widmo dyfrakcyjne (obraz dyfrakcyjny) siatki znacznie wyraźniejsze.

Siatki dyfrakcyjne odgrywają bardzo ważną rolę w wielu przyrządach stosowanych w nauce i technice. Szczególnie często siatki są wykorzystywane do otrzymywania światła monochromatycznego lub do rozszczepiania światła i analizy widm.

Podział siatek dyfrakcyjnych:

• siatki odbiciowe - odbijające świadtło (efekt zbliżony wizualnie do rozszczepienia światła przez płyty CD)

• siatki transmisyjne - przepuszczające światło (tworzone przez nacinanie rys lub ich wypalanie w metalu oraz metody holograficzne i fotograficzne):

• siatki transmisyjne amplitudowe - z liniami kolejno nieprzezroczystymi (ciemnymi) i szczelinami (przezroczystymi, przepuszczalnymi).

• siatki amplitudowe prostokątne - ich profil zmiany stopnia zaczernienia prostopadle do wiąski jest skokowy (prążki są wyraźne i powstaje wiele maksimów interferencyjnych);

• siatki amplitudowe sinusoidalne - ich profil zmiany stopnia zaczernienia prostopadle do wiązki jest łagodny (prążki są mniej wyraźne i powstają jedynie trzy maksima interferencyjne: n=0 i n=±1)

• siatki transmisyjne fazowe - w całym swoim obszarze przezroczyste dla światła, a odpowiednikami naprzemian przezroczystych i nieprzezroczystych linii siatki amplitudowej są tu linie o okresowo zmiennej grubości ośrodka;

• siatki fazowe prostokątne

• siatki fazowe sinusoidalne

Ze względu na to, że siatki dyfrakcyjne stosuje się głównie do uginania światła, ważnym parametrem siatek dyfrakcyjnych jest ich wydajność dyfrakcyjna η, którą definiuje się jako stosunek natężenia światła ugiętego w pierwszym rzędzie dyfrakcyjnym I₁ do całkowitego natężenia światła padającego na siatkę I₀.

Dyspersja kątowa siatki dyfrakcyjnej jest miarą zdolności siatki do rozszczepiania światła polichromatycznego na wiązki monochromatyczne. Można ją wyrazić wzorem:

,

gdzie:

Δλ - różnica między długościami fal padających na siatkę dyfrakcyjną

Δθ - różnica kątów ugięcia między falą λ a λ+Δλ

Dyspersja wzrasta wraz z rzędem widma m i jest odwrotnie proporcjonalna do stałej siatki d.

Chromatyczna zdolność rozdzielcza siatki, podobnie jak i pryzmatu, jest miarą zdolności rozdzielenia dwóch blisko siebie leżących linii widmowych o długościach fali λ i λ + ∆λ. Jeżeli obrazy dyfrakcyjne w m-tym rzędzie dyfrakcji tych dwóch linii są na tyle rozsunięte, że maksimum jasności jednej linii przypada na najbliższe minimum drugiej linii, to można pokazać, że zachodzi równość

Zależność ta, pozwala określić najmniejszą różnicę długości fali dwóch linii spektralnych, które można rozdzielić w m-tym rzędzie dyfrakcji za pomocą siatki o N szczelinach. Zdolność rozdzielcza R siatki dyfrakcyjnej mówi ile razy długość fali λ jest większa od rozdzielanego przedziału Δλ. Można ją zwiększyć używając siatki o większej liczbie szczelin N lub wykorzystując wyższe rzędy dyfrakcji m>1. Należy zwrócić uwagę na fakt, że chromatyczna zdolność rozdzielcza, w przeciwieństwie do dyspersji kątowej jest niezależna od stałej siatki d.

3. Układ pomiarowy

Zestaw przyrządów, którymi dysponowaliśmy podczas ćwiczeń:

• siatka dyfrakcyjna 50 1/m

• filtry interferencyjne 525nm, 640nm oraz filtr o nieznanej długości fali

• oświetlacz z zasilaczem

• ekran ze skalą i szczeliną

• ława optyczna z podziałką

Do zasilacza podłączamy oświetlacz, do którego montujemy wybrany filtr interferencyjny. Oświetlacz umieszczamy w taki sposób, aby promienie świetlne padały prostopadle do ekranu i siatki dyfrakcyjnej, umieszczonych na ławie optycznej. Wszystkie elementy oraz sposób ich rozmieszczenia pokazane są na schemacie poniżej.

4. Przebieg pomiarów

Na ławie optycznej umieściliśmy siatkę dyfrakcyjną w odległości L od ekranu, wynoszącej kolejno 20cm,30cm,40cm oraz 50cm. Odległość między siatką a ekranem zmierzyliśmy dzięki podziałce umieszczonej na ławie optycznej. Następnie do oświetlacza zamontowaliśmy filtr, dzięki któremu uzyskaliśmy długość fali 650nm. Po skierowaniu oświetlacza wraz z odpowiednim filtrem na ekran (jak na schemacie powyżej), patrząc przez siatkę dyfrakcyjną mogliśmy zaobserwować świecącą szczelinę w ekranie i jej pozorne obrazy na tle ekranu ze skalą. Następnie przy pomocy ruchomych wskazówek przymocowanych do ekranu odczytaliśmy położenia l_m i p_m pozornych obrazów szczeliny tworzonych przez promienie ugięte m-tego rzędu. Wszystkie powyższe pomiary powtórzyliśmy także dla filtrów 525nm oraz o nieznanej długości fali.

5. Tabele pomiarowe

Tabela 1 - wyznaczanie stałej siatki dyfrakcyjnej

gęstość linii siatki [1/mm]	λ [nm]	L [cm]	lm [mm]	pm [mm]	sinθm	Δsinθm	(sinθm)śr	Δ(sinθm)śr	d [μm]	Δd [μm]	δd [%]	dśr [μm]	Δdśr [μm]
50	650	20	-5,5	6	0,0287	0,0051	0,0304	0,0006	22,62	4,043	17,88	21,37	2,38
				30	-8,5	10			0,0308	0,0034					21,09	2,348	11,13
				40	-12	13			0,0312	0,0026					20,81	1,715	8,24
				50	-15	16			0,0310	0,0021					20,98	1,394	6,65
			525	20	-5	5,5			0,0262	0,0051	0,0255			0,0003	20,01	3,908	19,53	20,63	2,64
				30	-7	8			0,0250	0,0034					21,01	2,869	13,66
				40	-9,5	11			0,0256	0,0026					20,49	2,049	10,00
				50	-12	13			0,0250	0,0020					21,01	1,721	8,19

Tabela 2 - wyznaczanie długości fali światła przepuszczonego przez nieznany filtr

gęstość linii siatki [1/mm]	L [cm]	lm [mm]	pm [mm]	sinθm	Δsinθm	(sinθm)śr	Δ(sinθm)śr	dśr [μm]	Δd [μm]	λ [nm]	Δλ [nm]	λśr [nm]	Δλśr [nm]	δλśr [%]
50	20	-5,5	7	0,0312	0,0051	0,0304	0,0033	21	2,5	655,2	149,3	638,9	155,6	22,79
		30	-8,5	10	0,0308					0,0034								646,8	147,4
		40	-11	12	0,0287					0,0026								602,7	137,3
		50	-15	16	0,0310					0,0021								651	148,4

błąd pomiaru wartości ΔL, Δ l_m oraz Δp_m wynosi 1mm, czyli 0,001m

6. Przykładowe obliczenia

Obliczenia wykonane dla pierwszego wiersza tabeli 1 oraz pierwszego wiersza tabeli 2.

- obliczanie wartości sinθ_m i jego błędu bezwzględnego

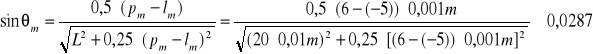
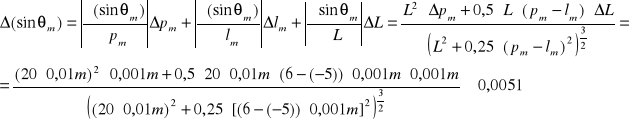
- obliczanie wartości średniej sinθ_m oraz błędu bezwzględnego na podstawie odchylenia standardowego od tej średniej

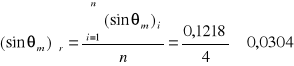
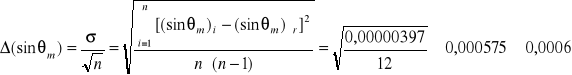
- obliczanie wartości stałej siatki dyfrakcyjnej d oraz jej błędu bezwzględnego i względnego

ponieważ λ przyjmujemy za stałe, więc błąd względny wyznaczenia d wynosi:

stąd:

Wartość średnią stałej siatki dyfrakcyjnej oraz wartość średnią błędu bezwzględnego wyznaczenia stałej siatki dyfrakcyjnej oblicza się analogicznie jak wartość średnią sinθ_m

- obliczanie długości fali λ oraz błędu bezwzględnego

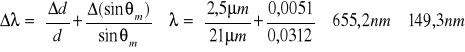
Pozostałe wartości, tj. λ_śr, Δλ_śr, oraz δλ_śr oblicza się analogicznie jak inne tego typu wartości obliczone powyżej.

7. Wnioski

W trakcie całego doświadczenia nie udało nam się zaobserwować na ekranie drugiego rzędu dyfrakcji, dlatego ilość pomiarów jest mniejsza a także błąd końcowy wyniku wyznaczenia stałej siatki dyfrakcyjnej d jest większy. Najprawdopodobniej siatka była siatką amplitudową sinusoidalną. Wszystkie zaobserwowane pozorne obrazy szczeliny położone były blisko szczeliny rzeczywistej, dlatego kąt θ, a co za tym idzie również sinθ miały małą wartość. Wartości bezwzględnych błędów pomiaru Δl_m oraz Δp_m były natomiast względnie duże w odniesieniu do zmierzonych wartości l_m i p_m. Zauważalnym skutkiem tych czynników jest bardzo wysoka wartość błędu wyznaczenia wartości stałej siatki dyfrakcyjnej Δd, wynosząca w skrajnym przypadku nawet ponad 19%. Dodatkowym czynnikiem wpływającym na wartość błędu była niedoskonałość ludzkiego oka.

Także użyta przez nas w doświadczeniu siatka dyfrakcyjna o gęstości linii 1/50mm nie jest siatką o najwyższej jakości. Ponieważ siatka ma małą gęstość linii, więc otrzymana wartość stałej d wynosząca około 21μm wydaje się być poprawna.

Oczywistym skutkiem otrzymania wysokiego błędu Δd jest również wysoka wartość błędu wyznaczenia nieznanej długości fali Δλ, wynosząca w przybliżeniu 22,8%.

Wartości błędów otrzymanych wyników mogłyby być niższe, gdyby w pomiarach użyć lepszej siatki dyfrakcyjnej oraz gdyby udało się zaobserwować na ekranie prążki interferencyjne drugiego rzędu dyfrakcji. Wówczas uzyskany kąt θ byłby większy (dla m=2), względny błąd wyznaczenia stałej sin θ byłby mniejszy, a zatem błąd względny wyznaczenia stałej d byłby również mniejszy.

1

Politechnika Wrocławska

Ugięcie światła na siatce dyfrakcyjnej

Schemat układu pomiarowego

---