1. Metody wyznaczania współczynnika ściśliwości s.

Prowadzimy pomiary filtracji pod różnymi ciśnieniami, a następnie wyznaczamy stałe C i K dla dwóch różnych ciśnień.

I -

II -

Znaleźć s znając stałe C₁, K₁, C₂, K₂:

c, k - stałe wartości

2. Przemywanie osadu.

Celem przemywania osadu jest usunięcie resztek cieczy filtrowanej z kapilar i przestrzeni międzyziarnowych warstw osadu (osad jest produktem lub filtrowana ciecz jest szczególnie cenna) -układ filtracyjny o znanych parametrach K i C oraz ciecz przemywająca o znanej lepkości

-prowadzimy filtrację przy Δp= const i T= const

- po zakończonej filtracji następuje przemywanie przy tej samej wartości Δp.

Opór, jaki stawia cieczy mającej osad i przegroda jest taki sam jak dla filtratu w ostatnim momencie filtracji: (dV/dτ)_f =K/(2*(V_f+C)). Ponieważ filtrat i ciecz przemywającą mogą mieć równą lepkość, to szybkość przemywania:

(A) (dV/dτ)_p=(dV/dτ)_f*μ_f/μ_p

(B) μ_f= μ_p ) (dV/dτ)_p=(dV/dτ)_f. Równania A I B są słuszne, jeśli Δp filtracji i przemywania są takie same, jeśli nie należy przeliczyć stałe K i C dla wartości Δp przemywania. τ_p= V_p/(dV/dτ)_p

V_p-wymagana objętość cieczy przemywającej, wyznaczana doświadczalnie

3. Wyprowadź zależność opisującą

strumień ciepła przewodzonego

przez ściankę płaską jednowarstwową

i opisz rozkład temperatury w

ściance płaskiej jednowarstwowej.

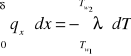
Rozkład temperatury przy przewodzeniu

ciepła przez ściankę płaską jest liniowy

i można zapisać go równaniem:

Rozkład temperatury w ściance płaskiej jest prostoliniowy.

4. Wyprowadź zależność opisującą strumień ciepła przewodzonego przez ściankę cylindryczną i opisz rozkład temperatur w tej ściance.

Q_h= qdA A=2πrL q= -λ(dT/dr)

Q_h= -λ2πrL(dT/dr)

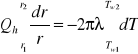
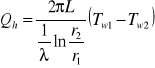
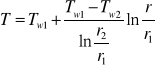
Rozkład temperature logarytmiczny

Dla ścianek płaskich wielowarstwowych.

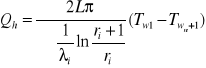
5. Omów konwekcję naturalną w

przestrzeni nieorganicznej.

Związana z ruchem płynu wywołanym różnicą temperatur między powierzchnia, z którą się styka płyn i wymienia z nią ciepło, a temp płynu. Różnica temp. Różnej części strumienia powoduje zmianę gęstości płynu. Powoduje ona powstanie w płynie dodatniej lub ujemnej siły wyporu. Siła wyporu powoduje ruch płynu wzdłuż powierzchni w kierunku pionowym, co powoduje powstanie konwekcyjnego ruchu ciepła. Jeśli płyn ogrzewamy to jego temp jest wyższa przy ściance i zgodnie z zasadą prądu płynu unosi się do góry, a na jego napięcie dopływa chłodniejszy. Przy chłodzeniu płynu jest odwrotnie. Wyróżniamy wnikanie ciepła w ruchu uwarstwionym, przejściowym i burzliwym.

6. wyprowadź zależność opisującą gęstość strumienia cieplnego przy przenikaniu ciepła przez ściankę płaską jedno- i wielowarstwową.

Jednowarstwowa: -ruch ciepła przez ściankę jest ustalony w czasie -Geometria ciała przewodzącego ciepło jest prosta -Przepływ ciepła w jednym kierunku -Temp. Ciała nie zależy od czasu

-Izotropia, jednorodna płyta o stałym λ. Strumień ciepła wnikający do ściany i od ściany do płynu: Q_h1=α₁A(T₁-T_w1) Q_h3=α₂A(T_w2-T₂)

Strumień ciepła przewodzonego przez ścianę:Q_h2=λ/σA(T_w1-T_w2)

Ustalony ruch ciepła: Q_h1= Q_h2= Q_h3= Q_h=const, zatem T₁-T_w1= Q_h/ α₁A T_w1-T_w2= Q_hσ/( λA)

T_w2-T₂= Q_h/ α₂A

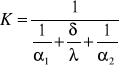
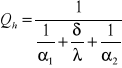
Q_h=KA(T₁-T₂) q=K(T_w1-T_w2)

Wielowarstwowa: q=KΔT=K(T₁-T₂)

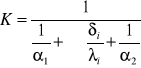
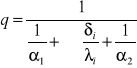
Q_h=KA(T₁-T₂)

7. Bilans materiałowy i cieplny półki teoretycznej.

Bilans materiałowy- G_n+1+L_n-1=G_n+L_n dla składnika bardziej lotnego: G_n+1x_n+1+ L_n-1y_n-1= G_nx_n+L_ny_n

Bilans cieplny: G_n+1i^”_n+1+ L_n-1i^'_n-1= G_ni^”_n+L_ni^'_n

jeśli: i^”_n=i^'_n+r_n ; i^”_n+1=i^'_n+1+r_n+1

i^'_n+1≈ i^'_n≈i^'_n-1≈i

to: (G_n+1+L_n-1)i^'-( G_n+L_n)i^'= G_nr_n- G_n+1r_n+1

jeśli: G_nr_n≈ G_n+1r_n+1 r_n+1≈r_n≈r_n-1≈r

G_n+1≈ G_n≈ G_n-1≈G

To: Gy_n+1+Lx_n-1=Gy_n+Lx_n wtedy: G(y_n- y_n+1)=L(x_n-1- x_n) lub L/G=(y_n- y_n+1)/ (x_n-1- x_n)=tgα

8. Przedstaw równanie, omów przebieg

podaj metody wykreślania linii operacyjnej

dla górnej części kolumny rektyfikacyjnej.

G=L+D← bilans materiałowy

G_n+1=Lx_n+Dx_D← dla składnika bardziej lotnego

gdy x_n, y_n+1 potraktujemy jako zmienne bieżące

y=L/(L+D)*x_n+(D/(d+L))*x_D

Metody wykreślania: - Znamy x_D I L/G=tgα

-Kreślimy prostą przez 2 punkty o danych współrzędnych. Gdyby retryfikat nie był dobierany to L=G, a nie linia operacyjna pokrywa się z przekątną. Po wykreśleniu górnej linii operacyjnej rysujemy konieczne półki.

9. Przedstaw równanie omów przebieg i

podaj metody wykreślania linii operacyjnej

dla dolnej części kolumny rektyfikacyjnej.

L^'=G' + W ←bilans materiałowy

Metody wykreślania:znajdujemy współrzędne przecięcia z przekątną x_w i y_w.Gdyby ciecz nie była odprowadzana (W=0) wtedy tgα'=1 i przebieg danej linii operacyjnej pokrywałby się z przekątną.

10. Przedstaw równanie linii e, omów jej

przebieg dla różnych wartości liczby e

i podaj metody jej wyznaczania.

Równanie prostej będącej miejscem geometrycznego przecięcia się górnej i dolnej linii operacyjnej w zależności od stanu cieplnego surówki.

Szukamy przecięcia przekątnych współrzędnych (x_w, y_w):

y=x

---