Zasada ciągłości zbioru liczb rzeczywistych.

A] każdy niepusty i ograniczony z góry zbiór liczb rzecz. ma kres górny

B] każdy niepusty i ograniczony z dołu zbiór liczb rzecz. ma kres dolny

- wzór de Moivre'a

,k=0,1,...,n-1

Definicja 10.

Niech (X,d) będzie przestrzenią metryczną, p₀∈X, r>0 kulę otwartą (domkniętą) o środku w punkcie p₀ i promieniu r nazywamy zbiór

Definicja 11.

Niech (X, d) będzie przestrzenią metryczną

1] Otoczeniem punktu p₀∈X nazywamy każdą kulę otwartą o środku w punkcie p₀. Promień tej kuli nazywamy promieniem tego otoczenia.

2] Punkt p nazywamy punktem skupienia zbioru E⊂X jeśli w każdym otoczeniu tego punktu istnieje punkt q≠p, q∈E.

3] Jeśli p∈E i p nie jest punktem skupienia zbioru E, to p nazywamy punktem _______ zbioru E.

4] Zbiór E nazywamy domkniętym jeśli każdy punkt skupienia tego zbioru należy do E.

5] Punkt p nazywamy punktem wewnętrznym zbioru E jeśli istnieje takie otoczenie K(p,r) tego punktu takie że K(p,r)⊂E (tzn. jeśli p∈E wraz z pewnym swym otoczeniem).

6] Zbiór E nazywamy otwartym jeśli każdy punkt zbioru E jest jego punktem wewnętrznym.

7] Dopełnieniem zbioru E do przestrzeni X nazywamy zbiór E'=X\E={p∈X:p∉E}

8] Zbiór E nazywamy ograniczonym jeśli istnieje kula (otwarta lub zamknięta) zawierająca ten zbiór.

9]Zbiór E nazywamy gęstym w X jeśli każdy punkt przestrzeni X∈E lub jest punktem skupienia tego zbioru.

Twierdzenie 20.

Zbiór G jest otwarty ⇔ gdy jego dopełnienie jest zbiorem domkniętym, zbiór F jest domkniętym ⇔ gdy jego dopełnienie jest zbiorem otwartym.

Definicja 12.

Pokryciem otwartym zbioru E w przestrzeni metrycznej zbioru X nazywamy rodzinę {G_α} zbiorów otwartych w przestrzeni X spełniających warunek

Zbiór zwarty.

Jeśli każde pokrycie otwarte zbioru K zawiera podpokrycie skończone (tzn. jeśli dla każdego pokrycia otwartego {G_α} zbioru K istnieje skończona liczba wskaźników α₁,α₂,...,α_n takich, że K⊂G_α1∪...∪G_αn)

Zbiór spójny.

Podzbiór E przestrzeni metrycznej X nazywamy zbiorem spójnym jeśli nie istnieją dwa zbiory A i B otwarte w przestrzeni X, rozłączne mające niepuste części wspólne ze zbiorem E (tzn. A∩E≠∅ i B∩E≠∅) i takie że E⊂A∪B.

Twierdzenie Weierstrassa.

Każdy nieskończony ograniczony podzbiór przestrzeni R^k ma punkt skupienia w R^k.

Definicja 13.

Ciąg {p_n} punktów przestrzeni metrycznej X nazywamy zbieżnym w tej przestrzeni jeśli istnieje punkt p∈X taki że

Fakt zbieżności ciągu {p_n} można zapisać

Definicja 14.

Ciąg {p_n} nazywamy ograniczonym, gdy zbiór wartości tego ciągu (tj. zbiór punktów p_n) jest ograniczony.

Ciąg {p_nj} nazywamy podciągiem ciągu {p_n}, jeśli ciąg {p_n} jest zbieżny bo jego granicę nazywamy granicą częściową ciągu {p_n}.

Warunek Couchego (ciąg Couchego)

Ciag {p_n} w przestrzeni metrycznej X nazywamy ciągiem couchego jeśli:

Twierdzenie 21.

Każdy ciąg zbieżny w przestrzeni metrycznej jest ciągiem Couchego.

Definicja 24.

Przestrzeń metryczną X nazywamy zupełną jeśli każdy ciąg Couchego w tej przestrzeni jest zbieżny.

Definicja 25.

Niech {x_n} będzie ciągiem w R. Mowimy że ten ciąg jest rozbieżny do +∞ (co zapisywaliśmy:

Jeśli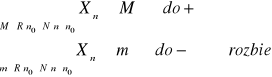

Twierdzenie o trzech ciągach.

Jeśli {x_n}, {y_n}, {z_n} są ciągami w R² i x_n≤y_n≤z_n dla prawie wszystkich n oraz
, to

Kryterium zbieżności Couschego.

Szereg
jest zbieżny ⇔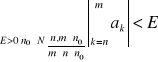

Warunek konieczny zbieżności szeregu.

Jeśli szereg
jest szeregiem zbieżnym to

Kryterium Couchego.

Niech dany będzie szereg
i niech

1] Jeśli α<1 to szereg
jest zbieżny

2] Jeśli α>1 to szereg
jest rozbieżny

Dowód 1]. Ponieważ α<1 więc istnieje β∈R takie że α<β<1 z ________ wynika że istnieje z kolei takie n₀∈N że
tzn.

Lecz 0≤α≤β<1 a więc szereg
jest szeregiem geometrycznym zbieżnym i w konsekwencji
jest także zbieżny na mocy z tw.25a

2] Jeśli α>1 wtedy dla nieskończenie wielu wyrazów ciągu {a_n} spełniona jest nierówność |a_n|>1

Istnieje podciąg
ciągu
jest zbieżny do α. A więc w otoczeniu
znajdują się prawie wszystkie wyrazy ciągu
. A więc nieskończenie wiele wyrazów ciągu

Nieskończenie wiele wyrazów tego ciągu spełnia nierówność
bowiem
dla α>1 skąd |a_n|>1 dla nieskończenie wiele wyrazów ciągu {a_n}. Oznacza to że ciąg {a_n}nie jest zbieżny do 0. I tym samym
jest rozbieżny, gdyż nie spełnia warunku koniecznego.

Szereg
nazywamy bezwzględnie zbieżnym jeśli szereg jest zbieżny. Jeśli szereg
jest zbieżny bezwzględnie to jest zbieżny. Jeśli szereg jest zbieżny, ale nie jest zbieżny bezwzględnie to nazywamy go warunkowo zbieżnym.

Def. Iloczynem Couchego szeregu
i
nazywamy szereg
gdzie,
n=0,1...n

Kryterium porównawcze.

A] Jeśli |a_n|≤c_n dla prawi wszystkich n i jeśli szereg
jest zbieżny to szereg
jest zbieżny.

B] Jeśli a_n≥d_n≥0 dla prawie wszystkich n i jeśli szereg
jest rozbieżny to szereg
jest rozbieżny.

Kryterium d'Alamberta.

Niech a_n≠0, n∈N szereg

A] Jest zbieżny jeśli granica górna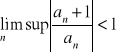

B] Jest rozbieżny jeśli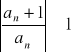
dla prawie wszystkich n.

Kryterium Dirichleta a_n∈C.

Jeśli sumy częściowe szeregu
są ograniczone zaś
jest nierosnący i zbieżny do zera ciągiem liczb rzeczywistych to
jest zbieżny.

Kryterium Abela'.

Jeśli szereg
(a_n∈C) jest zbieżny natomiast
jest monotoniczny (nie rosnący albo nie malejący) i ograniczonym ciągiem liczb rzeczywistych to szereg
jest zbieżny.

Kryterium Abela''.

Jeśli szerg
jest dowolnym szeregiem rozbieżnym o wyrazach dodatnich natomiast
jest zdefiniowany
jest ciągiem sum częściowych tego szeregu to szereg
jest dla α>1 zbieżny, a dla α≤1 rozbieżny.

Kryterium Leibniza.

Jeśli
jest nierosnącym ciągiem liczb rzeczywistych zbieżnym do zera, to szereg
jest zbieżny (szereg taki nazywamy szeregiem naprzemiennym).

Def. Szereg
nazywamy bezwzględnie zbieżnym jeśli szereg
jest zbieżny.

Tw. Jeśli szereg
jest zbieżny bezwzględnie to jest zbieżny.

Def. Jeśli szereg jest zbieżny ale nie jest zbieżny bezwzględnie to nazywamy go warunkowo zbieżnym.

Tw. Mertensa (po iloczynie couchego)

Jeśli szeregi
i
są zbieżne odpowiednio do sum A i B przy czym jeden z nich jest zbieżny bezwzględnie to iloczyn Couchego tych szeregów jest zbieżny do sumy. C=A*B

Tw. Riemanna.

Niech szereg
, a_n∈R, n∈N będzie zbieżnym warunkowo i niech α≤β; α,β∈R wtedy istnieje takie przestawienie porządku składników że szereg
o sumach częściowych S'_n ma własności:

Szereg bezwzględnie zbieżny.

- zbieżny,
- rozbieżny

Def. Mówimy że szereg jest zbieżny bezwarunkowo jeżeli każda zmiana porządku jego wyrazów daje szereg zbieżny (do tej samej sumy).

Tw. Niech dany jest szereg
, a_n∈C, n∈N, szereg
jest zbieżny bezwarunkowo wtw. gdy jest zbieżny bezwzględnie.

Tw. Brouwera.

Jeśli
gdzie
jest domkniętą kulą Euklidesową w Rⁿ, jest odwzorowaniem ciągłym to f posiada punkt stały w
.

Tw. Zasada kontrakcji Banacha.

Niech X=(x,d) będzie przestrzenią metryczną zupełną i niech f:X→X będzie odwzorowaniem takim że istnieje 0≤α<1 takie że:

d[f(x),f(y)]≤α*d(x,y) dla wszystkich x,y∈X wtedy funkcja posiada w X dokładnie jeden punkt stały.

Granica i ciągłość funkcji.

Def. Couchego granicy funkcji.

Niech (X,dx),(y,dy) będą przestrzeniami metrycznymi E⊂X. Niech dalej f:E→Y, p-punkt skupienia zbioru E. Mówimy że q∈Y jest granicą funkcji f w punkcie p lub że f dąży do q, gdy x dąży do p (co zapisujemy)

jeśli:

---