W ramach prac nad dostosowaniem procesu kształcenia na SGH do założeń deklaracji bolońskiej pojawiły się głosy na temat konieczności zmniejszenia liczby godzin z matematyki. W celu sprawdzenia, jak na tą kwestię zapatrują się studenci, przeprowadzono sondę. Losowo wybranych 600 studentów starszych lat zapytano, czy popierają tą propozycję, czy też są przeciw niej. Wyniki przeprowadzonej sondy były następujące:
|
Za |
Przeciw |
Student |
250 |
50 |
Studentka |
200 |
100 |
Czy dane uzyskane z badania uprawniają do stwierdzenia, że występuje zależność między płcią studenta a jego opinią w kwestii zmniejszenia liczby godzin z matematyki? Jeśli tak, to, jaka jest siła tej zależności w badanej próbie? [3]
Jeśli założymy, że prawdopodobieństwo poparcia propozycji zmniejszenia liczby godzin z matematyki przez mężczyznę wynosi 0,85, jakie jest prawdopodobieństwo, że wśród pytanych 1600 studentów płci męskiej ogółem ze wszystkich lat poprze propozycję co najwyżej 1360? [2]
Z jakiego twierdzenia należało skorzystać rozwiązując podpunkt 1.2 ? [1]
1.4. Podaj estymator punktowy dla odsetka osób będących przeciw pomysłowi zmniejszenia liczby godzin z matematyki [1].
Jaką rozpiętość będzie miał przedział, który w 99 przypadkach na 100 będzie zawierał odsetek przeciwników pomysłu zmniejszenia liczby godzin z matematyki wśród wszystkich studentów starszych lat? [3]
1.6. W jaki sposób można zwiększyć precyzję estymacji przedziałowej otrzymanej w punkcie poprzednim (odpowiedz bez wykonywania dodatkowych obliczeń)? [1]
1.7. W jaki sposób można sprawdzić, czy odsetki przeciwników i zwolenników projektu na SGH obojga płci istotnie różnią się od siebie? (zaproponuj metodę i zapisz odpowiednie hipotezy wraz ze wzorem na statystykę testującą) [3]
Poniższe rysunki przedstawiają przybliżone rozkłady płac mężczyzn (linia grubsza ) i kobiet (linia cieńsza ) pracujących w 2005 roku w firmie „Promote”.
2.1. Na powyższym rysunku zaznacz przybliżone położenie średniej i mediany dla każdego z rozkładów. Według jakiej zasady zaznaczyłeś położenie średniej? [2]
2.2. Na podstawie rysunku wypowiedz się na temat kierunku asymetrii rozkładu płac kobiet. (odpowiedź uzasadnić) [1]
2.3. Porównaj oba rozkłady płac pod względem poziomu przeciętnego, zróżnicowania i asymetrii (porównaj również siłę asymetrii)? [2]
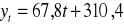
Liczbę reklam Cudownych Środków na Katar emitowanych w telewizji publicznej cechuje stały wzrost oraz multiplikatywne wahania sezonowe. W celu oszacowania odpowiedniej funkcji trendu zebrano kwartalne dane o liczbie emitowanych reklam (yt) w ciągu ostatnich 3 latach (2003-2005). Oszacowano następującą funkcję trendu:
t=0,1,…,11
Dodatkowo zaobserwowano, że w każdych I, II oraz IV kwartałach na skutek działania czynników sezonowych liczba emitowanych reklam Cudownych Środków na Katar jest wyższa o odpowiednio: 34%, 3% oraz 5% w stosunku do poziomu wynikającego z trendu liniowego zaś w kwartałach III jest niższa od poziomu wynikającego z trendu..
3.1. Jaki był wpływ czynników sezonowych na liczbę emitowanych reklam w III kwartałach? [1]
3.2. Czy współczynnik oszacowanej funkcji trendu na poziomie istotności 0,05 okazał się statystycznie istotny, jeśli krytyczny poziom istotności wyniósł 0,0017? (odpowiedź uzasadnić) [2]
3.3. Czy można z całą pewnością stwierdzić, że decyzja podjęta w punkcie wcześniejszym jest słuszna? (odpowiedź uzasadnić) [1]
3.4. Jakich danych brakuje w powyższym przykładzie do oceny wielkości wahań przypadkowych? [1]
3.5. Jakiej teoretycznie liczby reklam należy oczekiwać w III kwartale obecnego roku? (Nie obliczając standardowego błędu prognozy, zinterpretuj uzyskany wynik) [2]
CZĘŚĆ TESTOWA (12 punktów)
UWAGA: We wszystkich pytaniach dla każdej z podanych odpowiedzi należy wskazać, czy jest ona prawidłowa (wpisując x w kolumnie "TAK"), czy nieprawidłowa (wpisując x w kolumnie "NIE").
Punktacja: odpowiedź poprawna 1 pkt; brak odpowiedzi 0 pkt; odpowiedź błędna -1 pkt.
Jeżeli całkowita suma punktów z części testowej będzie ujemna, jako wynik części testowej zostanie przyjęte 0 pkt.
|
TAK |
NIE |
1. Posłużenie się statystyką t (Studenta) w teście istotności dla wartości oczekiwanej przy małej próbie: |
|
|
a/ wymaga aby badana zmienna miała rozkład normalny, |
|
|
b/ nie jest wskazane, |
|
|
c/ wymaga aby wariancja w populacji generalnej była znana. |
|
|
2. Rozkład Poissona: |
|
|
a/ może być wykorzystany do opisu rozkładu liczby zgłoszeń wypadków samochodowych, |
|
|
b/ jest najczęściej symetryczny, |
|
|
c/ może być wykorzystany do opisu rozkładu jedynie cech skokowych. |
|
|
3. Testując hipotezę |
|
|
a/ Na pewno nie można odrzucić hipotezy zerowej, jeżeli hipoteza alternatywna ma postać |
|
|
b/ Ze względu na powyższy wynik należy zapisać hipotezę alternatywną w postaci |
|
|
c/ Jeżeli wariancje obu zmiennych w populacji generalnej nie są znane, to decyzja czy odrzucić H0 na rzecz |
|
|
4. Wartość współczynnika korelacji liniowej rxy w próbie losowej wyniosła 0. Oznacza to, że: |
|
|
a/ zmienne X i Y są niezależne, |
|
|
b/ nie należy stosować modelu regresji liniowej do prognozowania wartości Y na podstawie wartości X, |
|
|
c/ wartość współczynnika korelacji liniowej ρ w populacji generalnej nie może być różna od zera. |
|
|
EGZAMIN termin 3 ZESTAW B
1
![]()
x
ni
Wyszukiwarka
Podobne podstrony:
egz CC 2011 06 25(SdS)
02 06 2012 statystyka notatkiid504
ANALIZA STRUKTURY ROZKŁADU JEDNOWYMIAROWEGO(2), SGH, statystyka
statystyka -pytania egz, SZKOŁA, semestr II, GWSH Statystyka
Tura2-b, SGH, statystyka
Statystyka 07.06.2009, Statystyka
SIMR-AN1-EGZ-2011-09-06-rozw
Statystyka 21.06.2009, Statystyka
ANALIZA STRUKTURY ROZKŁADU JEDNOWYMIAROWEGO, SGH, statystyka
egz mo teoria 06
statystyka+egz+z+12.02.2011+-+rozwiazania, STATYSTYKA
opracowanie pytan egz z kpa u adamiakowej 06-07, Akty prawne KPA
egz CC 2011 06 25(SdS)
więcej podobnych podstron