Nr ćwiczenia 82 |
Temat ćwiczenia Efekt fotoelektryczny |
Ocena z teorii |
Nr zespołu 10 |
Imię i Nazwisko Miłosz Gąsiorowski |
Ocena z wykonania |
Data 27.03.2001 |
Wydział, kierunek, rok, grupa EAIiE, Automatyka i Robotyka, rok 1, gr.2 |
Uwagi |
Cel ćwiczenia.
Celem ćwiczenia jest obserwacja efektu fotoelektrycznego: wybijania elektronów z metalu przez światło o różnej częstości (barwie). Pomiar energii kinetycznej wybitych elektronów umożliwia obliczenie wartości stałej Plancka oraz pracy wyjścia elektronów.
Wstęp teoretyczny.
Podczas oświetlania metalowej płytki, światłem o odpowiednio dużej częstotliwości, zostaną z niej wybite tzw. fotoelektrony. Zjawisko to posiada kilka charakterystycznych cech:
ilość wybitych elektronów zależy od częstotliwości światła i dla każdego materiału istnieje graniczna częstotliwość poniżej, której to zjawisko nie zachodzi,
istnieje maksymalna wartość energii kinetycznej fotoelektronów i zależy ona od częstotliwości światła i rodzaju wykorzystanego materiału.
![]()
Okazuje się, że fotony uderzając w elektrony przekazują im własną energię, umożliwiając tym emisję poza materiał. Istnieje pewna graniczna energia, jaką musi posiadać elektron, aby opuścić metal. Jeżeli więc fotony będą posiadać energię równa różnicy tej wartości i energii odpowiadającej poziomowi Fermiego, może dojść do tego zjawiska. Jakakolwiek nadwyżka energii przekazana elektronowi będzie obserwowalna jako jego energia kinetyczna. Możemy łatwo zauważyć, że energia fotonu jest wyrażona jako:
![]()
gdzie h - stała Plancka, a f - częstotliwość światła, to by doszło do zjawiska, częstotliwość światła musi przekroczyć pewną graniczną wartość. Energia kinetyczna elektronów jest więc równa:
gdzie W - to praca wyjścia elektronu z metalu. Istnieje zatem maksymalna wartość tej energii. Będą ją posiadały elektrony, które w chwili zderzenia z fotonem znajdowały się na poziomie Fermiego. Wynika z tego także, że wartość tej energii będzie zależała od rodzaju materiału (wielkości pracy wyjścia) i częstotliwości światła (energia fotonu).
Maksymalną energie kinetyczną Ekmax można mierzyć , dobierając takie napięcie U=Uh , że mierzony prąd I zmaleje do zera, i to napięcie mierzymy. Wtedy to praca eUh równa jest Ekmax.
![]()
Stąd mamy liniową zależność napięcia hamowania od częstotliwości światła f:
Nachylenie prostej dopasowanej do punktów eksperymentalnych Uh(f) wynosi h/e daje zatem możliwość dopasowania stałej Plancka h. Przecięcie prostej z osią poziomą odpowiada częstości granicznej f0=W/h
Wykonanie ćwiczenia.
u
4) Opracowanie wyników, dyskusja błędów
![]()
Ogólna związek wyników w zależności liniowej:
Wzory na wyliczenie współczynników zależności liniowej, mając n par punktów pomiarowych xi yi zależnych liniowo.
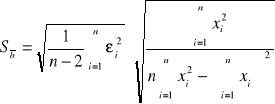
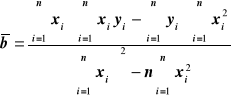
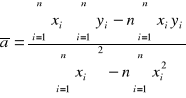
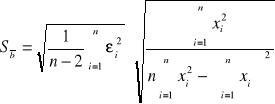
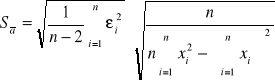
Sposób wyliczenia odchylenia standardowego:
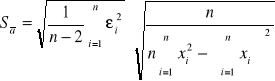
![]()
5) Wnioski
![]()
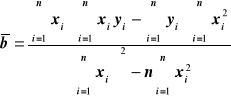
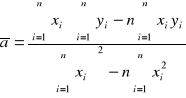
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
labolatorium2, agh wimir, fizyka, Fizyka(1)
10 moj konspekt, agh wimir, fizyka, Fizyka(1)
konspekt(1), agh wimir, fizyka, Fizyka(1)
samoindukcja cewki, agh wimir, fizyka, Fizyka(1)
Kospekt teoria, agh wimir, fizyka, Fizyka(1)
labolatorium4, agh wimir, fizyka, Fizyka(1)
tabele9, agh wimir, fizyka, Fizyka(1)
22wstep, agh wimir, fizyka, Fizyka(1)
Opracowanie 10, agh wimir, fizyka, Fizyka(1)
fizyka 2, agh wimir, fizyka, Fizyka
22opr, agh wimir, fizyka, Fizyka(1)
ZESTAW2A, agh wimir, fizyka, fiza
7 konspekt, agh wimir, fizyka, Fizyka(1)
konspekt Cw5, agh wimir, fizyka, Fizyka(1)
lab22wyniki, agh wimir, fizyka, Fizyka(1)
Mikrofale do druku, agh wimir, fizyka, Fizyka(1)
więcej podobnych podstron