Numer ćwiczenia: 7
|
Temat ćwiczenia: Samoindukcja cewki |
Ocena z teorii: |
Numer zespołu 21
|
Nazwisko i imię: Witkowicz Jakub
|
Ocena zaliczenia ćwiczenia: |
Data: 02.03.2004
|
Wydział: EAIiE Rok: I Grupa: 7 |
Uwagi:
|
Cel ćwiczenia:
Wyznaczenie współczynnika samoindukcji cewki poprzez porównanie impedancji dla prądu zmiennego i rezystancji dla prądu stałego.
Wymagane wiadomości teoretyczne:
prawo Ohma (I=U/R) - mówi, że opór rozważanego przewodnika jest zawsze taki sam, niezależnie od wielkości napięcia przyłożonego w celu zmierzenia go. Prawo Ohma nie stanowi jednak ogólnego prawa elektromagnetyzmu, gdyż jest specjalną własnością pewnych materiałów.
prawo indukcji Faradaya - jest jednym z podstawowych równań elektrodynamiki i głosi, że indukowana w obwodzie siła elektromotoryczna (SEM) równa jest wziętej ze znakiem ujemnym szybkości zmian strumienia ΦB indukcji magnetycznej przechodzącego przez ten obwód. Prawo to zapisujemy w postaci:
ε = -dΦB/dt (∫Edl = -dΦB/dt).
samoindukcja cewki - jest to zjawisko pojawiania się indukowanej SEM (siły elektromotorycznej samoindukcji) w pojedynczej cewce, kiedy w niej samej zmienia się prąd. Jak każda indukowana SEM podlega prawu indukcji Faradaya, które dla np. dla ściśle nawiniętej cewki przyjmuje postać ε = -d(NΦB)/dt (N - liczba zwojów, NΦB - wypadkowy strumień przechodzący przez wszystkie zwoje). Iloczyn NΦB jest ważną wielkością charakterystyczną dla indukcji. Dla danej cewki, oddalonej od wszelkich materiałów magnetycznych wielkość ta jest proporcjonalna do natężenia prądu i płynącego w cewce:
NΦB = Li, gdzie L jest stałą proporcjonalności, nazywaną indukcyjnością cewki.
ε = -d(NΦB)/dt = -Ldi/dt, z czego otrzymujemy
L = -ε/(di/dt) [L]=1henr [H]=1Vs/A.
rezystancja - (opór elektryczny czynny) jest to stosunek różnicy potencjałów na końcach elementu elektrycznego do natężenia prądu przepływającego przez niego. Jest to zatem miara oporu, jaki dany element stawia przepływowi ładunku elektrycznego. Rezystancja przewodu jest wprost proporcjonalna do jego długości, a odwrotnie proporcjonalna do jego przekroju.
R = U/I [R] = 1Ω (om)
reaktancja - (opór bierny) jest właściwością obwodu elektrycznego zawierającego pojemność elektryczną, która wraz z oporem czynnym tworzy opór elektryczny pozorny. W szczególnym przypadku szeregowo połączonych elementów o indukcyjności L i pojemności C wypadkowa reaktancja wynosi X = ωL-1/(ωC), (ω - pulsacja prądu zmiennego).
impedancja - czyli opór pozorny Z jest dany wzorem Z2 = R2 + X2, gdzie R jest oporem czynnym danego obwodu, a X oporem biernym.
konduktancja - przewodność elektryczna czynna przewodnika w obwodzie prądu stałego co do wartości równa odwrotności wartości rezystancji G = 1/R, [G] = 1S (simens)
susceptancja - przewodność elektryczna bierna (B)
admitancja - (przewodność elektryczna pozorna) pojęcie wprowadzane przy przepływie przez przewodnik prądu sinusoidalnie zmiennego, jest wielkością zespoloną, której moduł jest równy |Y| = ![]()
przesuniecie fazowe - miedzy zmiennym napięciem i prądem występuje w obwodzie elektrycznym zawierającym oprócz oporu czynnego także opór bierny,
np. jeżeli do kondensatora przyłożymy napięcie sinusoidalnie zmienne:
U(t) = U0cos(ωt),
to zgodnie z równaniem Q = CU ładunek kondensatora też będzie zmieniał się
w czasie:
Q(t) = CU0cos(ωt),
zmiana ładunku kondensatora oznacza, że do jego okładek dopływa lub odpływa ładunek, czyli płynie prąd przemienny. Ponieważ I = dQ/dt, więc podstawiając wcześniejszą zależność i obliczając pochodną otrzymujemy:
I(t) = -ω C U0 sin(ωt).
Z czego wynika, że prąd chwilowy I(t) ma charakter sinusoidalny, podobnie jak naięcie U(t) na kondensatorze, lecz czasowo wyprzedza w fazie napięcie o kąt π/2.
częstotliwość - f, υ, liczba pełnych cykli drgań okresowych w jednostce czasu określona w hercach (Hz) liczbowo równa odwrotności okresu drgań
częstość - liczba określonych zdarzeń zachodzących w jednostce czasu
Wykonanie ćwiczenia:
1. Zestawić układ według podanego schematu - podłączyć pierwszą cewkę, ustawić
mierniki na właściwy tryb pracy (pomiar prądu i napięcia stałego na zakresie 2 A i 20 V).
2. Podłączyć źródło napięcia stałego, sprawdzić czy zakresy przyrządów są optymalnie
dobrane.
3. Zmieniając napięcie potencjometrem zmierzyć zależność prądu od napięcia I=(U=)
(kilkanaście par punktów pomiarowych z zakresu 0÷12 V).
4. Wyłączyć zasilanie, podłączyć drugą cewkę i powtórzyć dla niej pomiar charakterystyki I=
(U=) dla prądu stałego.
5. Odłączyć zasilanie prądem stałym, podłączyć transformator.
6. Skorygować ustawienie amperomierza (mniejsze prądy spowodowane reaktancją cewki
wymagają być może zmniejszenia zakresu pomiarowego).
7. Zmierzyć zależność prądu zmiennego od napięcia I~(U~) podobnie jak w punkcie 3.
8. Wyłączyć transformator i przekonfigurować układ w celu pomiaru pierwszej cewki.
Opracowanie wyników
Cewka1
prąd stały: prąd zmienny:
U[V] |
I[mA] |
||
1 |
32 |
||
2 |
64 |
||
3 |
96 |
||
4 |
129 |
||
5 |
160 |
||
6 |
193 |
||
7 |
225 |
||
8 |
257 |
||
9 |
289 |
||
10 |
321 |
||
11 |
352 |
||
12 |
383 |
||
U[V] |
I[mA] |
||
1 |
2,46 |
||
2 |
4,4 |
||
3 |
6,15 |
||
4 |
7,73 |
||
5 |
9,21 |
||
6 |
10,61 |
||
7 |
11,94 |
||
8 |
13,2 |
||
9 |
14,4 |
||
10 |
15,58 |
||
11 |
16,7 |
||
12 |
17,8 |
||
Uśr = 6,5[V], Iśr = 208[mA] Uśr = 6,5[V], Iśr = 10,85[mA]
Cewka 2
prąd stały: prąd zmienny:
U[V] |
I[mA] |
||
1 |
72 |
||
2 |
143 |
||
3 |
214 |
||
4 |
286 |
||
5 |
356 |
||
6 |
428 |
||
7 |
498 |
||
8 |
566 |
||
9 |
636 |
||
10 |
704 |
||
11 |
762 |
||
12 |
826 |
||
U[V] |
I[mA] |
||
1 |
5,2 |
||
2 |
9,4 |
||
3 |
13 |
||
4 |
16,2 |
||
5 |
19,4 |
||
6 |
22,2 |
||
7 |
25 |
||
8 |
27,6 |
||
9 |
30 |
||
10 |
32,5 |
||
11 |
34,9 |
||
12 |
37 |
||
Uśr = 6,5[V], Iśr = 457,58[mA] Uśr = 6,5[V], Iśr = 22,7[mA]
Obliczam szukane wartości dla cewki nr 1:
(korzystam z wyliczonych wartości średnich)
dla prądu stałego: R = ![]()
R = ![]()
= 31,25[![]()
]
dla prądu zmiennego: Z = ![]()
= 599[![]()
]
Z = ![]()
![]()
![]()
598[![]()
]
L = ![]()
, ![]()
, f = 50[Hz] L = 1,9[H]
Błąd ![]()
L wyznaczenia współczynnika samoindukcji cewki L obliczam z prawa przenoszenia niepewności, gdyż nasza szukana jest wielkością złożoną oraz ilość pomiarów pozwala mi z niej korzystać.
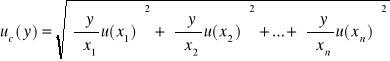
L(Z,R), gdzie: L = 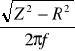
,
![]()
jest wartością stałą
zakładam, że:
ΔU = 0,01[V], ΔI = 1[mA] - dla prądu stałego i ΔI = 0,1[mA] - dla prądu zmiennego
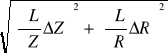
ΔL =
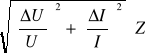
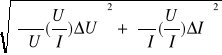
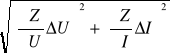
ΔZ = = =
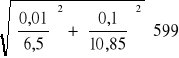
ΔZ = = 5,59[![]()
]
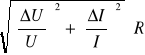
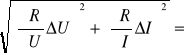
ΔR =
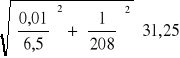
ΔR = = 0,15[![]()
]
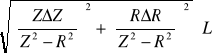
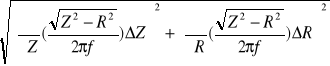
ΔL = =
ΔL = 0,017 [H]
Szukam kąta przesunięcia fazowego:
tg![]()
= ![]()
= ![]()
![]()
= arctg(![]()
) ![]()
![]()
= 870
Analogiczne obliczenia dla cewki nr 2 prowadzą do uzyskania wyników:
dla prądu stałego: R = 14,2[![]()
]
dla prądu zmiennego: Z = 286,34[![]()
]
![]()
285,98[![]()
]
L =0,91[H]
zakładam, że:
ΔU = 0,01[V], ΔI = 1[mA] - dla prądu stałego i ΔI = 0,1[mA] - dla prądu zmiennego
ΔZ = 1,33[![]()
]
ΔR = 0,04[![]()
]
ΔL = 0,004 [H]
![]()
= arctg(![]()
) ![]()
![]()
= 87,150
Wnioski i uwagi:
1
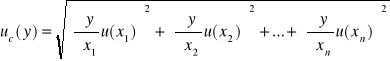
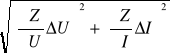
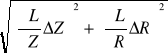
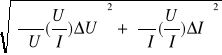
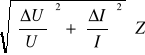
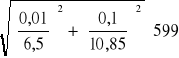
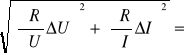
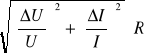
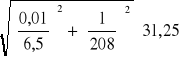
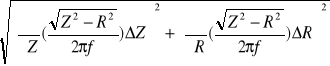
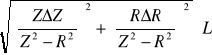
Wyszukiwarka
Podobne podstrony:
samoindukcja cewki wyniki, agh wimir, fizyka, Fizyka(1)
samoindukcja cewki projekt, agh wimir, fizyka, Fizyka(1)
labolatorium2, agh wimir, fizyka, Fizyka(1)
10 moj konspekt, agh wimir, fizyka, Fizyka(1)
konspekt(1), agh wimir, fizyka, Fizyka(1)
Ćw 7. Samoindukcja cewki, Laboratoria, Laboratorium Fizyka
Kospekt teoria, agh wimir, fizyka, Fizyka(1)
labolatorium4, agh wimir, fizyka, Fizyka(1)
tabele9, agh wimir, fizyka, Fizyka(1)
22wstep, agh wimir, fizyka, Fizyka(1)
Opracowanie 10, agh wimir, fizyka, Fizyka(1)
fizyka 2, agh wimir, fizyka, Fizyka
22opr, agh wimir, fizyka, Fizyka(1)
ZESTAW2A, agh wimir, fizyka, fiza
7 konspekt, agh wimir, fizyka, Fizyka(1)
konspekt Cw5, agh wimir, fizyka, Fizyka(1)
więcej podobnych podstron