NIEPEWNOŚCI POMIAROWE

1. Niepewność bezwzględna

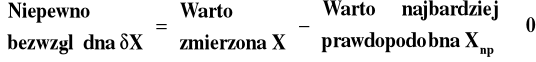
(1)

2. Wynik pomiaru

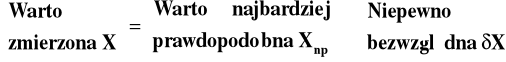
(2)

Z relacji (2) wynika, że:

• najlepszym przybliżeniem wartości mierzonej jest wg eksperymentatora liczba X_np oraz

• z rozsądnym prawdopodobieństwem szukana wielkość znajduje się gdzieś pomiędzy X_np - δ i X_np + δ.

3. Reguła podawania niepewności i podawania wyniku

Niepewności eksperymentalne powinny być zwykle zaokrąglane:

• do jednej cyfry znaczącej, jeśli pierwsza cyfra znacząca jest większa od 2,

• do dwóch cyfr znaczących, jeśli pierwsza cyfra znacząca wynosi 1 lub 2,

• ostatnia cyfra znacząca w wyniku powinna zwykle być tego samego rzędu (stać na tym samym miejscu dziesiętnym) co niepewność pomiaru.

4. Niepewność względna

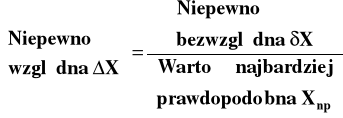
(3)

Niepewność względna zwana jest także dokładnością, najczęściej wyrażaną w procentach.

Jest ona przybliżoną wskazówką jakości pomiaru:

• niepewności względne rzędu 10% są charakterystyczne dla zgrubnych pomiarów,

• niepewności względne rzędu 1% czy 2% charakteryzują pomiary dokładne.

Liczba cyfr znaczących w liczbie wyrażającej wynik pomiaru lub obliczeń jest przybliżonym wskaźnikiem dokładności wyznaczenia tej liczby.

Weźmy pod uwagę dwie liczby

X₁=510 i X₂=0,55.

Niepewność bezwzględna pierwszej wynosi: 5, a względna 1%, natomiast stosowne niepewności liczby drugiej wynoszą: 0,025 i 4,5%.

5. Klasa dokładności przyrządu pomiarowego

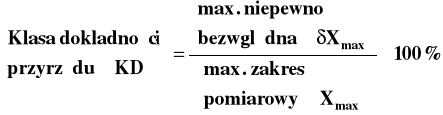
(4)

Przykład

Zmierzono temperaturę powietrza przy pomocy elektrycznego termometru rezystancyjnego o klasie dokładności KD = 0,5 (0,5%) i maksymalnym zakresie T_max=200°C. Termometr wskazał temperaturę 125°C. Jaka jest maksymalna niepewność pomiaru ? Podać poprawnie wynik pomiaru, używając niepewności bezwzględnej i względnej.

Maksymalna wartość niepewności bezwzględnej wynosi

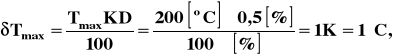
a względnej będzie

,

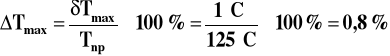
natomiast wynik należy przedstawić w postaci T = 125 ± 1°C lub T = 125°C ± 0,8%.

6. PRAWA PRZENOSZENIA NIEPEWNOŚCI

6.1. Niepewność sumy i różnicy

Jeśli dodaje się lub odejmuje pewną liczbę wielkości: X_k i Y_j

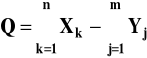
to niepewność bezwzględna wyniku (liczby Q) jest zawsze sumą niepewności bezwzględnych wielkości X_k i Y_j

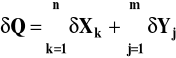
(5)

6.2. Niepewność iloczynu i ilorazu

Jeśli mnoży się lub dzieli pewną liczbę wielkości: X_k i Y_j

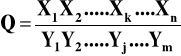
to niepewność względna wyniku (liczby Q) jest zawsze sumą niepewności względnych wielkości X_k i Y_j

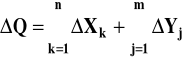
(6)

6.3. Niepewność iloczynu wielkości mierzonej i dokładnej liczby

Jeśli wielkość X została zmierzona z niepewnością bezwzględną δX i używana jest do obliczenia iloczynu Q = BX, przy czym δB = 0, to niepewność bezwzględna Q ma wartość

(7)

6.4. Niepewność wyrażenia potęgowego

Jeśli wielkość X, zmierzona z niepewnością względną ΔX, jest używana do obliczenia wyrażenia potęgowego
to niepewność względna Q ma wartość

(8)

1. Przykłady obliczeniowe

Zadanie 1.

Należy poprawnie obliczyć następujące wyniki pomiarów podając wartość najbardziej prawdopodobną oraz niepewności bezwzględną i względną:

1. zmierzona wielkość L = 5,03 ± 0,0436 m;

2. zmierzona średnica D = 62.34 ± 0,075 mm oraz D = 125,35 ± 1,26 mm;

3. zmierzony czas t = 20,5431 ± 1 s;

4. zmierzony współczynnik przewodzenia ciepła λ = 0,05254 ± 0,000254 W/(mK);

5. zmierzona długość fali λ = 0,000000563 ± 0,00000007 m;

6. zmierzona gęstość ρ = 138,58 ± 1,5 kg/m³;

7. zmierzona wilgotność próbki X = 2,5 ± 0,251 %.

Zadanie 2

Próbkę z wełny mineralnej należy nagrzać od temperatury T₁ do T₂. Temperaturę próbki mierzono termometrem rtęciowym o elementarnej działce 1°C, a czas nagrzewania zegarkiem z sekudnikiem. Uzyskano następujące wyniki: temperatura początkowa T₁= 20°C, temperatura końcowa T₂= 105°C, czas początkowy t₁=12h 30min 0s, czas końcowy t₂=12h 58min 45s.

Należy obliczyć: przyrost temperatury próbki ΔT i czas nagrzewania próbki Δt wraz z bezwzględną i względną niepewnościami pomiarowymi.

Zadanie 3

Kalkulator wyświetla wynik 123,123. Jaka będzie niepewność bezwzględna i względna tego wyniku, jeśli zdecydowaliśmy się, że ma on tylko trzy cyfry znaczące? To samo obliczenie powtórzmy dla liczb 0,123123 oraz 321,321.

Zadanie 4

Zmierzono wymiary prostopadłościennej próbki metalowej uzyskując następujące wyniki: długość L = 550 ± 10 mm, szerokość S = 225 ± 5 mm oraz wysokość H = 25 ± 2 mm. Należy określić całkowite pole powierzchni próbki A oraz objętość próbki wraz z niepewnościami: względną i bezwględną. Z jakimi dokładnościami należałoby mierzyć wymiary próbki, aby niepewność względna nie przekraczała 1%?

Zadanie 5

Dane są wyniki następujących pomiarów: a = 50±10mm; b=0,18±0,02cm; c=12±1cm; t=3,0±0,5s; m=0,018±0,001kg. Należy obliczyć następujące wielkości oraz ich dokładności pomiarów; a + b + c; a + b - c; ct; 4ab; (ab)/2 oraz (mb)/t².

Zadanie 6

Wykorzystując prawa przenoszenia niepewności wykonaj następujące obliczenia:

1. (5 ± 1) + (8 ± 2) - (10 ± 4),

2. (5 ± 1)⋅(8 ± 4),

3. 
   

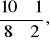
4. 2⋅π⋅(10,54 ± 0,5),

5. 
   .

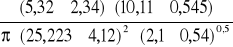
Dr inż. Andrzej Puszer 1

Katedra Energetyki Procesowej

STEROWANIE PROCESAMI TECHNOLOGICZNYMI

---