METODY PODEJMOWANIA DECYZJI

Podejmowanie decyzji jest podstawową funkcją kierowania systemem eksploatacji dla podjęcia optymalnej decyzji niezbędne jest posiadanie określonego zbioru informacji charakteryzującego system lub jego element, którego dana decyzja dotyczy. Proces decyzyjny realizowany jest zazwyczaj z wykorzystaniem modelu decyzyjnego opisującego system, odpowiednio do zastosowanej metody.

Matematyczny model decyzyjny:

MMD = <D,R,Z,F,P>

D - dziedzina modelu - zbiór obiektów, elementów rzeczywistości i wielkości, których model dotyczy

R- relacje modelu - zbiór zależności między elementami dziedziny modelu

Z - założenia modelu - zbiór ograniczeń nałożonych na dziedzinę i relacje modelu

F - kryterium modelu (funkcja celu) - kryterium optymalizacyjne podejmowanej decyzji

P - problem decyzyjny - pytanie (problem), na które model decyzyjny powinien umożliwić udzielenie odpowiedzi.

Przykład:

Przedsiębiorstwo produkcyjne wytwarza dwa wyroby: x₁ i x₂. Do ich produkcji wykorzystywane są dwie maszyny: m₁ i m₂. Liczba godzin pracy maszyny m₁ potrzebnych do wytworzenia jednej jednostki wyrobu x₁ wynosi 2 godziny, zaś wyrobu x₂ 1 godzinę, zaś maszyny m₂ odpowiednio 5 i 5 godziny. Przy czym ze względów technologicznych maszyna m₁ może pracować maksymalnie przez 12 godzin dziennie, zaś maszyna m₂ 40 godzin. Należy ustalić plan produkcji zapewniający maksymalny łączny przychód z ich sprzedaży wiedząc, iż, cena wyrobu x₁ wynosi 5 zł, zaś wyrobu x₂ 5zł.

Typ produktu			Zysk
		Maszyna m1	Maszyna m2
A - x1	2	5	5
B - x2	1	5	5
Czas pracy	12	40	-

Odpowiedź:

Należy ustalić plan produkcji zapewniający maksymalny łączny przychód z ich sprzedaży

Tak sformułowany problem decyzyjny opiszę za pomocą matematycznego modelu decyzyjnego wskazując jego elementy:

D - dziedzina modelu - wyroby typu A,B, maszyny, zysk z sprzedaży

R - relacje modelu - czas pracy maszyn potrzebny do wyprodukowania danego wyrobu i zysk przedsiębiorstwa z sprzedaży

Z - założenia modelu - czas pracy maszyn na dobę

F - kryterium modelu - maksymalizacja zysku przedsiębiorstwa

P - problem decyzyjny - maksymalna liczba sprzedanego wyrobu

Założenia modelu - funkcja celu

Z = 5x1+5x2 -> max

Warunki ograniczające

2x1+x2<=12

5x1+5x2<=40

Ze względu na charakter rozważanego problemu zmienne decyzyjne powinny przyjmować wartości nieujemne i całkowite.

X1,x2 >= 0

Rozwiązanie metodą graficzną

Z = 5x1+5x2 -> max

2x1+1x2<=12

5x1+5x2<=40

1. Ograniczenia sprowadzam do postaci odcinkowej równań prostych:

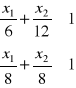
2. Obliczam współrzędne wektora grad Z:

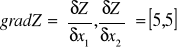
3.Wyznaczam kierunek i zwrot wektora grad Z

4. Wykres

Otrzymane rozwiązanie oznacza, że dla uzyskania maksymalnego dochodu w danych warunkach z sprzedaży, wówczas jej zysk będzie równy:

Z=5X1+5x2=5*4 + 5*4=40

Rozwiązanie metodą analityczną

1. przekształcam problem do postaci kanonicznej

2. Przekształcam problem do postaci standardowej

3. Warunki zadania przedstawiam w postaci tablicy liczbowej

4. Rozwiązanie zadania przedstawiam w postaci kolejnej tablicy liczbowej

4. Rozwiązanie zadania jest następujące

---