Dyskretne Przekształcenie Fouriera

Definicja

Odwzorowanie skończonego ciągu liczbowego

w ciąg liczb zespolonych

zgodnie ze wzorem

,
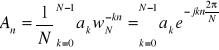
; gdzie

nazywamy Dyskretnym Przekształceniem Fouriera (Discrete Fourier Transform -DFT),

a odwrotne przekształcenie (Inverse Discrete Fourier Transform - IDFT) jest dane wzorem

,
.

Dla uniknięcia bardzo małych amplitud
, czynnik
jest często umieszczany we wzorze na IDFT. Wówczas otrzymamy następującą parę wzorów opisujących DFT:

,
;

,
.

Amplituda
nosi nazwę składowej stałej i przyjmuje wartość rzeczywistą. Pozostałe składowe przejawiają własność symetrii co do modułu (oś symetrii dla N parzystych znajduje się w punkcie o indeksie
, dla N nieparzystych pomiędzy punktami o indeksach
i
.

Przykład 1.

Wyznaczyć DFT następującego ciągu liczb: 1,2,3,4 (
).

-----------------------------------------------------------------

,

.

------------------------------------------------------------------

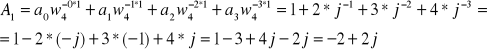
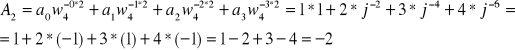
Zapis DFT i IDFT w postaci macierzowej

Niech

,

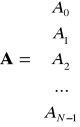
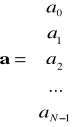
wówczas możemy zapisać

gdzie

,

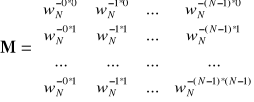
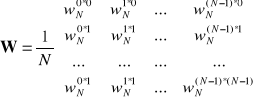
Przykład 2.

Wyznaczyć DFT następującego ciągu liczb (z przykładu 1): 1,2,3,4 (
).

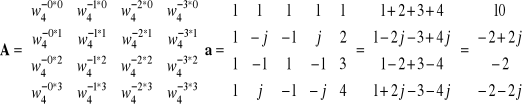
Dwuwymiarowa transformata Fouriera (DFT2)

W zastosowaniu do przetwarzania obrazów cyfrowych wykorzystuje się dwuwymiarowe przekształcenie Fouriera, będące naturalnym rozszerzeniem transformaty jednowymiarowej. Mamy w tym Przypadku do czynienia z przekształceniem macierzy liczb rzeczywistych U w macierz liczb zespolonych V zgodnie ze wzorem:

,
,

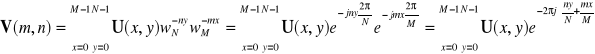
gdzie
,
.

Przekształcenie odwrotne natomiast dane jest wzorem:

,

,
.

Można zauważyć, iż dwuwymiarowe przekształcenie Fouriera DFT2 można uzyskać dokonując jednowymiarowych przekształceń DFT dla wierszy, a następnie dla kolumn (macierzy powstałej po transformacie wierszy), względnie odwrotnie.

3

---