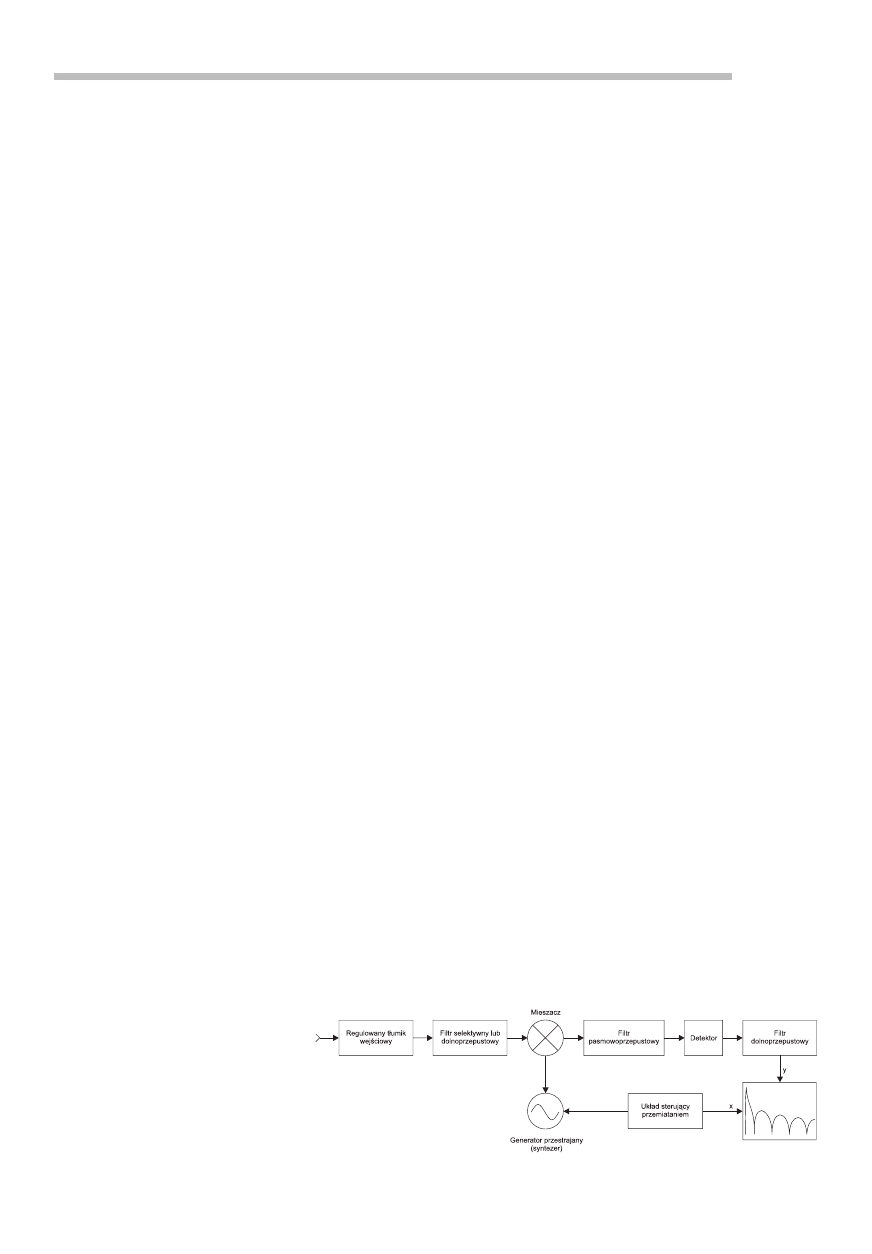
97

Elektronika Praktyczna 2/2006

K U R S

Ponieważ algorytm FFT jest po-

wszechnie stosowany w programach

do analizy układów elektronicznych

[2] oraz we współczesnych oscylo-

skopach cyfrowych, niezbędna dla

każdego elektronika staje się podsta-

wowa wiedza, pozwalająca na zro-

zumienie znaczenia poszczególnych

parametrów modyfikujących działa-

nie algorytmu szybkiej transforma-

ty Fouriera.

W cyklu trzech artykułów przed-

stawione zostaną problemy pojawia-

jące się podczas stosowania DFT,

jej pochodzenie i podstawy teore-

tyczne. Na zakończenie omówione

będą przykłady realizacji praktycz-

nej dyskretnego przekształcenia Fo-

uriera z zastosowaniem ogólnie do-

stępnego oprogramowania.

Metody analizy widma

Klasyczne analizatory widma

działają w oparciu o metodę wobu-

lacyjną, polegającą na przestrajaniu

lokalnego generatora wzorcowego

(najczęściej jest to syntezer często-

tliwości) i analizę widma w oparciu

o proces przemiany częstotliwości.

Schemat blokowy takiego analizato-

ra, przedstawiony na

rys. 1, przypo-

mina odbiornik superheterodynowy.

W efekcie przemiany częstotliwo-

ści, w takt zmian częstotliwości ge-

neratora przestrajanego, sygnał wej-

ściowy jest przesuwany względem

stałej częstotliwości środkowej fil-

tru pasmowo przepustowego o bar-

dzo wąskiej charakterystyce przeno-

szenia. Upraszczając mocno sprawę,

można stwierdzić, że jeśli w sygna-

le wejściowym znajdują się składo-

we częstotliwościowe mieszczące się

w paśmie przenoszenia filtra, detek-

Dyskretne przekształcenie

Fouriera,

część 1

Dyskretne przekształcenie Fouriera DFT (Discrete Fourier
Transform) jest, obok procedur filtracji cyfrowej, jednym
z podstawowych, a zarazem najbardziej skutecznych narzędzi
cyfrowego przetwarzania sygnałów. Poza istotnym znaczeniem
teoretycznym DFT odgrywa ważną rolę w zagadnieniach
związanych z układowymi realizacjami różnorodnych algorytmów
przetwarzania sygnałów. Wynika to z istnienia bardzo wydajnego
algorytmu obliczania dyskretnej transformaty Fouriera, zwanego
szybką transformatą Fouriera FFT (Fast Fourier Transform).

tor je wykrywa i na ekranie pojawia

się odpowiedni prążek.

Klasyczne analizatory widma do-

konują więc rzeczywistego pomiaru

widma analizowanego sygnału sto-

sując metodę pośrednią. Istnieją też

rozwiązania oparte o metodę bezpo-

średnią wykorzystujące odpowiednie

banki filtrów. Drugą grupę analiza-

torów stanowią urządzenia badają-

ce widmo w oparciu o operacje ma-

tematyczne wykonywane na prób-

kach zmierzonego sygnału wejścio-

wego. Te operacje to ciąg obliczeń

realizowany wg algorytmu FFT, czy-

li wydajniejszej obliczeniowo imple-

mentacji DFT [1]. Olbrzymi przyrost

mocy obliczeniowej, który dokonał

się w ostatnich latach, pozwolił na

zastosowanie techniki FFT jako opcji

praktycznie we wszystkich współ-

czesnych oscyloskopach cyfrowych.

Jest to zjawisko o tyle naturalne, że

w układzie takiego oscyloskopu musi

nastąpić cyfryzacja sygnału wejścio-

wego przed jego wizualizacją. Sko-

ro więc w pamięci pojawia się sy-

gnał wejściowy w postaci cyfrowej,

nic nie stoi na przeszkodzie, żeby

poddać go różnorodnym procedurom

CPS obliczającym m.in. jego wartość

średnią, skuteczną, międzyszczytową

i oczywiście reprezentację widmową.

Termin cyfrowe przetwarzanie

sygnałów – CPS (DSP – Digital Si-

gnal Processing

) [3, 4] pojawia się

coraz częściej w wielu, często za-

skakujących kontekstach, warto więc

w tym miejscu uściślić, co kryje się

pod tą nazwą. Pod pojęciem sygna-

łu rozumiemy pewną wielkość, któ-

ra na ogół ulega zmianom w czasie.

Sygnałem może być więc tempera-

tura, prędkość, natężenie oświetle-

nia itp. Klasycznie sygnał przedsta-

wiany jest w postaci graficznej jako

pewna funkcja czasu. Wymienio-

ne sygnały opisują procesy fizyczne

o naturze ciągłej, co powoduje, że

ich charakter musi być analogicz-

ny, czyli ciągły w czasie i wartości.

Z tego powodu sygnały takie nazy-

wane są analogowymi – są bezpo-

średnią analogią opisywanej przez

nie wielkości fizycznej.

Przetwarzanie takich sygnałów

jest utrudnione, gdyż układy ana-

logowe używane do tego celu są

wrażliwe na zmiany temperatury,

starzenie się elementów i wiele in-

nych czynników zakłócających, ta-

kich jak np. szumy czy tętnie-

nia sieci zasilającej. Stosując ukła-

dy analogowe, nie jesteśmy w sta-

nie zapewnić absolutnej powtarzal-

ności przetwarzania.

Sygnały cyfrowe, to sygnały, któ-

rych amplituda jest zdefiniowa-

na wyłącznie w określonych chwi-

lach (są to więc sygnały dyskretne

w czasie) i przedstawiana w postaci

liczb o skończonej precyzji. Sygna-

ły cyfrowe są więc dyskretne rów-

nież w amplitudzie

1

. Określenie cy-

frowe pochodzi właśnie od zapi-

su kolejnych dyskretnych wartości

chwilowych w postaci cyfr. Cyfrowe

przetwarzanie sygnałów można więc

zdefiniować jako analizę lub prze-

Rys. 1. Schemat blokowy klasycznego analizatora widma

Elektronika Praktyczna 2/2006

98

K U R S

kształcenie informacji przedstawionej

w postaci ciągu liczbowego. Przetwa-

rzanie cyfrowe, poza wieloma in-

nymi zaletami wynikającym z moż-

liwości bezpośredniego zastosowania

komputera, zapewnia pełną powta-

rzalność przeprowadzonej analizy.

Porównując współczesne analiza-

tory widma, można ogólnie stwier-

dzić, że rozwiązania bazujące na

FFT zapewniają lepszą dokładność

pomiaru amplitudy, lepszą rozdziel-

czość częstotliwościową i większą

szybkość pomiaru. Słabą stroną ana-

lizatorów „matematycznych” jest gor-

sza niż w analizatorach „przemiatają-

cych” dokładność pomiaru częstotli-

wości. Niebagatelną cechą analizato-

rów klasycznych jest ich olbrzymia

cena – kupując oscyloskop z wbu-

dowanym modułem FFT, analizator

widma mamy niejako za darmo.

Użytkownik nowiutkiego oscy-

loskopu cyfrowego z modułem FFT

zachęcony reklamami i, rzecz ja-

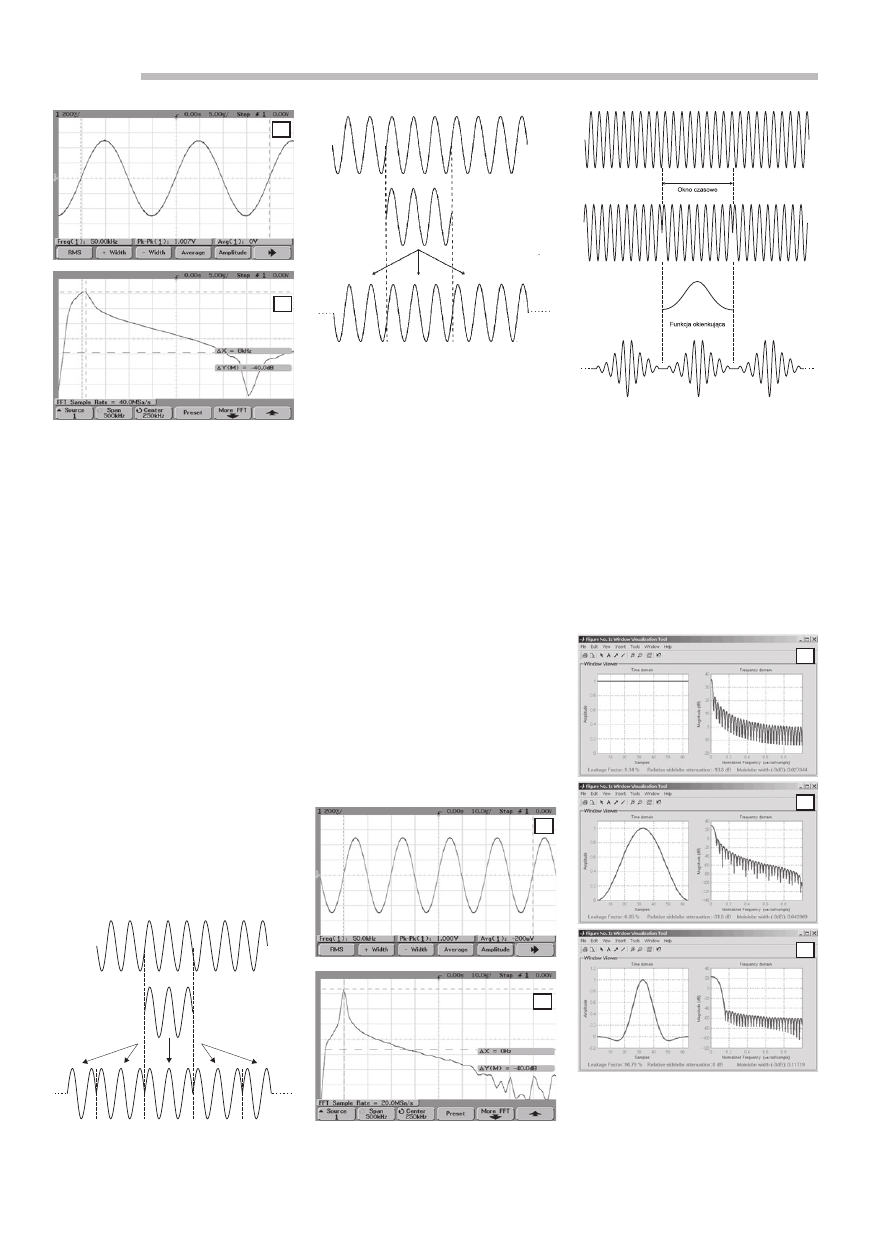
Rys. 3. Zniekształcenie sygnału wej-
ściowego na skutek wycięcia za po-
mocą okna prostokątnego

Rys. 2. Przebieg czasowy sygna-
łu harmonicznego o częstotliwości
50 kHz (a) i otrzymane widmo (b)

sna, faktycznymi potrzebami włącza

oscyloskop i przystępuje do pomia-

ru tzw. widma [5]. Pójdźmy tym

tropem i zmierzmy widmo czyste-

go sygnału harmonicznego o często-

tliwości np. 50 kHz. Spodziewamy

się oczywiście pojedynczego prążka

na częstotliwości 50 kHz.

Po podaniu na wejście oscylosko-

pu odpowiedniego sygnału otrzymu-

jemy oscylogram przedstawiony na

rys. 2a. Wybieramy z grupy funkcji

matematycznych FFT i otrzymujemy

widmo pokazane na

rys. 2b.

Rezultat eksperymentu w żaden

sposób nie przypomina pojedyncze-

go prążka, aczkolwiek zauważamy

maksimum energii na właściwej czę-

stotliwości. Okazuje się, że otrzyma-

ny wynik jest prawidłowy (!), tzn.

nie jest rezultatem wadliwego dzia-

łania sprzętu. Przed rozpoczęciem

pomiarów i próbą interpretacji wyni-

Rys. 4. Przypadek całkowitej liczby
okresów w prostokątnym okienku wy-
cinającym sygnał

Rys. 5. Przebieg czasowy sygnału
harmonicznego po korekcie podsta-
wy czasu (a) i otrzymane widmo (b)

Rys. 7. Charakterystyki czasowe i czę-
stotliwościowe najczęściej stosowa-
nych funkcji okien: a). okno prosto-
kątne, b). okno Hanninga (inaczej
podniesionego cosinusa, zwane czę-
sto oknem Hanna), c). okno Flat Top

Rys. 6. Proces „okienkowania” sygna-
łu wejściowego

ków musimy uświadomić sobie, co

właściwie mierzymy?

Oryginalne zależności Fouriera

operują na nieskończonych sygna-

łach czasowych i wówczas dla sy-

gnału harmonicznego otrzymujemy

– tak jak w rzeczywistości – poje-

dynczy prążek. W przypadku uru-

chomienia algorytmu DFT dysponu-

jemy zaledwie fragmentem sygnału

ograniczonym pewnym oknem pro-

a

b

a

b

b

a

c

99

Elektronika Praktyczna 2/2006

K U R S

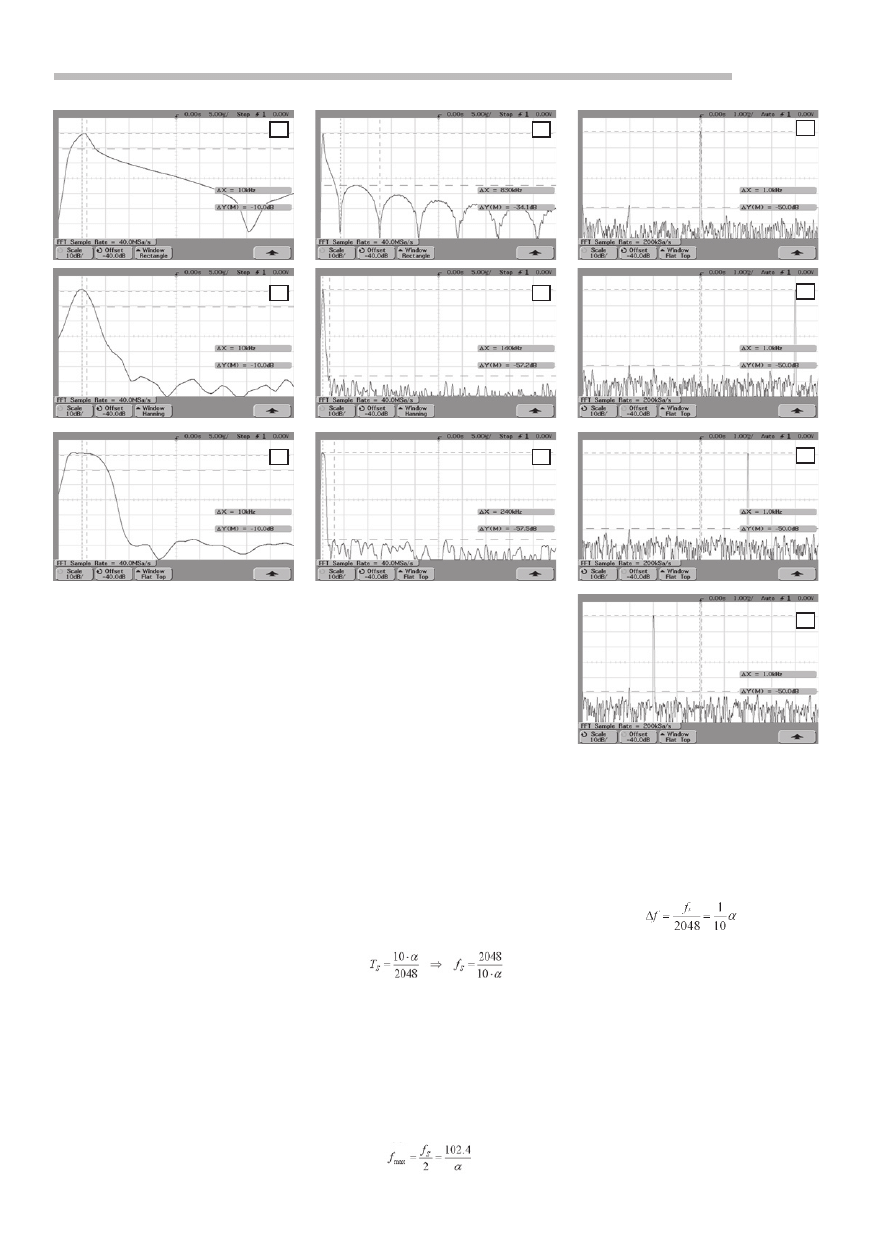
Rys. 8. Efekty zastosowania różnych
funkcji okien: a). okno prostokątne,
b). okno Hanninga, c). okno Flat Top

stokątnym

2

o długości N, a otrzy-

mane widmo jest widmem sygna-

łu złożonego z periodycznie powta-

rzającego się wycinka, co pokazano

na

rys. 3. Ponieważ wycinek sy-

gnału zaczyna się i kończy bardzo

gwałtownie jego widmo ulega istot-

nej modyfikacji. Szczegółowy i bar-

dzo przystępny opis tego zjawiska

jest przedstawiony w [3].

Analizując sytuację przedsta-

wioną na rys. 3, możemy dojść do

wniosku, że gdyby „wycinany” frag-

ment sygnału zawierał całkowitą

liczbę okresów – efekt zniekształ-

cenia nie powinien wystąpić. Przy-

padek taki zilustrowany jest na

rys. 4.

Jeśli więc sygnał wyświetlany na

ekranie oscyloskopu – który definiu-

je nasze okienko czasowe – będzie

zawierał całkowitą liczbę okresów, to

cykliczne powtarzanie takiego wycin-

ka da w efekcie sygnał taki sam jak

oryginalny sygnał wejściowy. W każ-

dym innym przypadku pojawią się

zniekształcenia przypominające modu-

lację, a właściwie manipulację, fazy.

Regulując podstawę czasu oscylosko-

pu, otrzymujemy oscylogram i widmo

przedstawione na

rys. 5.

Rys. 9. Efekty zastosowania różnych
funkcji okien obserwowane w szer-
szym spektrum: a). okno prostokątne,
b). okno Hanninga, c). okno Flat Top

Rys. 10. Ilustracja zjawiska aliasin-
gu (skala zobrazowania liniowa, za-
kres: 0...100 kHz). a). fwe = 50 kHz lub
fwe = 150 kHz, b). fwe = 90 kHz, c).
fwe = 130 kHz, d). fwe = 170 kHz

Zwróćmy uwagę, że jednocze-

śnie zmieniła się częstotliwość

próbkowania, która jest skorelowa-

na z podstawą czasu. Wynika to

z faktu, że w prostych oscylosko-

pach cyfrowych przyjęto stałą licz-

bę próbek rozkładaną równomier-

nie na cały ekran (standardowo 10

działek). Stosowany praktycznie al-

gorytm FFT operuje na liczbie pró-

bek będącej całkowitą potęgą licz-

by 2. Przyjmując, podobnie jak

np. w oscyloskopie Agilent 54621A,

liczbę próbek równą 2

11

= 2048,

okres i częstotliwość próbkowania

możemy wyrazić jako

gdzie a [s/dz.] oznacza podstawę

czasu oscyloskopu.

Zatem w rozważanym przypad-

ku częstotliwość próbkowania wyno-

si w przybliżeniu 20 MHz. W związku

z tym – co będzie wyjaśnione szcze-

gółowo w kolejnych częściach cyklu –

maksymalna częstotliwość możliwa do

obserwacji jest określona zależnością

a rozdzielczość częstotliwościowa

wynosi

Wynik otrzymany na rys. 5 jest

jak najbardziej zadowalający, ale

spryt, którym się wykazaliśmy nie

na wiele nam się przyda. Nie mo-

żemy zawsze ustawiać całkowi-

tej wielokrotności okresu na ekra-

nie, jeśli sygnał jest złożony, a je-

go zwartość widmowa nie jest zna-

na – przecież dopiero chcemy ją

określić. Efekt, który obserwujemy,

nosi nazwę przecieku i chociaż po-

każemy pewne środki zaradcze mi-

nimalizujące go, przecieku nie moż-

na wyeliminować całkowicie.

(1.1)

(1.2)

(1.3)

b

a

c

b

a

c

b

a

c

d

Elektronika Praktyczna 2/2006

100

K U R S

Okienkowanie sygnału

Skoro nieciągła zmiana sygnału na

krańcach przedziału próbkowania jest

powodem przecieku, to lekarstwem

będzie wycinanie sygnału za pomo-

cą okna o łagodnych zboczach. Mno-

żąc ciąg wejściowy przez funkcję tego

typu, powodujemy, że wartości sygna-

łu wynikowego stają się takie same na

początku i końcu przedziału próbko-

wania. Jednocześnie okienkowanie re-

dukuje moc sygnału i w konsekwen-

cji zmniejsza też amplitudy wszystkich

prążków widma, przy czym, ze wzglę-

du na łagodne „wygaszenie” sygnału

na końcach, minimalizuje najbardziej

jego składowe wysokoczęstotliwościowe

powodujące przeciek. Istotę okienkowa-

nia ilustruje

rys. 6.

W praktyce wykorzystuje się kilka

typowych funkcji, do których należą

m.in.: okno prostokątne, okno Hannin-

ga i tzw. okno Flat Top (maksymalnie

płaskie

3

). Przebiegi czasowe i widma

wymienionych funkcji przedstawione

są na

rys. 7. Każde z okien ma cha-

rakterystyczne właściwości, które najle-

piej poznamy, eksperymentując z wyko-

rzystaniem algorytmu szybkiej transfor-

maty Fouriera.

Ogólnie można stwierdzić, że wybór

okna stanowi pewien kompromis mię-

dzy szerokością listka głównego, pozio-

mem pierwszego listka bocznego i szyb-

kością malenia poziomu listków bocz-

nych ze wzrostem częstotliwości. Inny-

mi słowy, chodzi o kompromis między

dokładnością w określaniu amplitudy

i częstotliwości – jak wcześniej wspo-

mniano okienkowanie fałszuje ampli-

tudę sygnału. W porównaniu z oknem

prostokątnym, które z reguły traktowa-

ne jest jako odniesienie, okno Hannin-

ga zapewnia lepszą rozdzielczość czę-

stotliwościową kosztem pewnego pogor-

szenia dokładności pomiaru amplitu-

dy. Z kolei okno Flat Top, dzięki pła-

skiemu fragmentowi podstawowej linii

widmowej, poprawia dokładność okre-

ślania amplitudy kosztem pogorszenia

dokładności pomiaru częstotliwości.

Wróćmy do sytuacji początkowej

i wypróbujmy na naszym sygnale róż-

ne funkcje okienkujące. Wyniki takiego

eksperymentu pokazane są na

rys. 8.

Efekty zastosowania różnych okien

czasowych jeszcze wyraźniej zobaczy-

my, rozszerzając zakres częstotliwości,

w którym obserwujemy widmo. Usta-

wiając zakres na 5 MHz i częstotliwość

środkową na 2,5 MHz otrzymujemy zo-

brazowania pokazane na

rys. 9. Porów-

nując rysunki 7 i 9, możemy się naocz-

nie przekonać, że w istocie DFT bada-

nego sygnału nie jest faktycznie trans-

formatą tegoż sygnału, a jedynie aprok-

symacją splotu jego rzeczywistej trans-

formaty z transformatą funkcji okienku-

jącej sygnał.

Aliasing, czyli nakładanie się

widma

Przeprowadzając analizę widma za

pomocą procedur FFT, musimy pa-

miętać o konsekwencjach twierdzenia

o próbkowaniu. Rozważymy to szcze-

gółowo w drugiej części cyklu, w tej

chwili przyjmując jedynie do wiadomo-

ści, że maksymalna częstotliwość zawar-

ta w widmie sygnału poddawanego ana-

lizie nie może być większa od połowy

częstotliwości próbkowania. W przeciw-

nym przypadku nastąpi efekt „zawinię-

cia” widma i poważnego zafałszowania

wyniku pomiaru. Jedynym sposobem na

eliminację tego zjawiska jest zastosowa-

nie odpowiedniego filtru antyaliasingo-

wego, ograniczającego widmo sygnału

poddawanego próbkowaniu.

Przetestujmy niebezpieczeństwo zwią-

zane z aliasingiem, obniżając częstotli-

wość próbkowania do 200 kHz

4

. Zgod-

nie ze wzorem (1.1) częstotliwość prób-

kowania regulujemy, zmieniając podsta-

wę czasu oscyloskopu. Ustawiamy za-

kres obserwowanych częstotliwości na

100 kHz i przestrajamy generator sy-

gnałowy w granicach 50...200 kHz. Przy

zwiększaniu częstotliwości sygnału wej-

ściowego, dopóki nie przekracza ona fs/

2 = 100 kHz, prążek prawidłowo przesu-

wa się w prawo. Następnie, po przekro-

czeniu 100 kHz, zaczyna przesuwać się

z powrotem w lewo i przy 150 kHz po-

krywa się z prążkiem wynikającym z po-

dania na wejście sygnału o częstotliwo-

ści 50 kHz. Kilka przykładowych zrzu-

tów z ekranu oscyloskopu przedstawio-

no na

rys. 10.

Andrzej Dobrowolski

elka.wel.wat.edu.pl/~adobrowolski/

Literatura
1. Cooley J., Tuckey J., „An algorithm for the

machine computation of complex Fourier
series”, Math. Comput., vol. 19 (90), 1965

2. Dobrowolski A., „Pod maską SPICEa. Meto-

dy i algorytmy analizy układów elektronicz-
nych”, BTC, Warszawa, 2004

Lyons R. G., „Wprowadzenie do cyfrowego

przetwarzania sygnałów”, WKŁ, Warszawa,
1999

3. Oppenheim A. V., Schafer R. W., „Cyfro-

we przetwarzanie sygnałów”, WKŁ, Warsza-
wa, 1979

Szabatin J., „Podstawy teorii sygnałów”, WKŁ,

Warszawa, 2000

1

Wątek ten rozwiniemy w drugiej części cyklu.

2

Okno prostokątne jest wektorem złożonym

z N jedynek. Reszta wyrazów jest zerowa.

3

W dziedzinie częstotliwości.

4

W literaturze angielskojęzycznej często ope-

ruje się jednostką Sa/s, którą należy in-
terpretować dosłownie − jako liczba pró-
bek (

Sample) pobranych w ciągi sekundy.

W rozważanym przypadku 200 kHz ozna-
cza więc 200 kSa/s.