Elektronika Praktyczna 5/2006

98

K U R S

Dyskretne  przekształcenie 

Fouriera

,  część  3

Jeśli  rozpatrywany  sygnał  −  na-

zwijmy  go  x

C

1 

(

 

t

 

)  −  będzie  odwróco-

ny  w fazie,  to  również  wystąpi  peł-

na  korelacja,  w tym  sensie,  że  zmia-

nom  sygnału  x

C

1 

(

 

t

 

)  będą  towarzy-

szyły  dokładnie  przeciwne  zmiany 

sygnału  harmonicznego  cos

 

(2πft

 

), 

względem  którego  wyznaczamy  kore-

lację,  co  zilustrowano  na 

rys.  12.

Wyliczmy  zatem  odpowiednią 

całkę

 

(2.12)

Wynik  jest  zgodny  z oczekiwania-

mi  –  wartość  całki  jest  taka  sama, 

lecz  ma  przeciwny  znak.

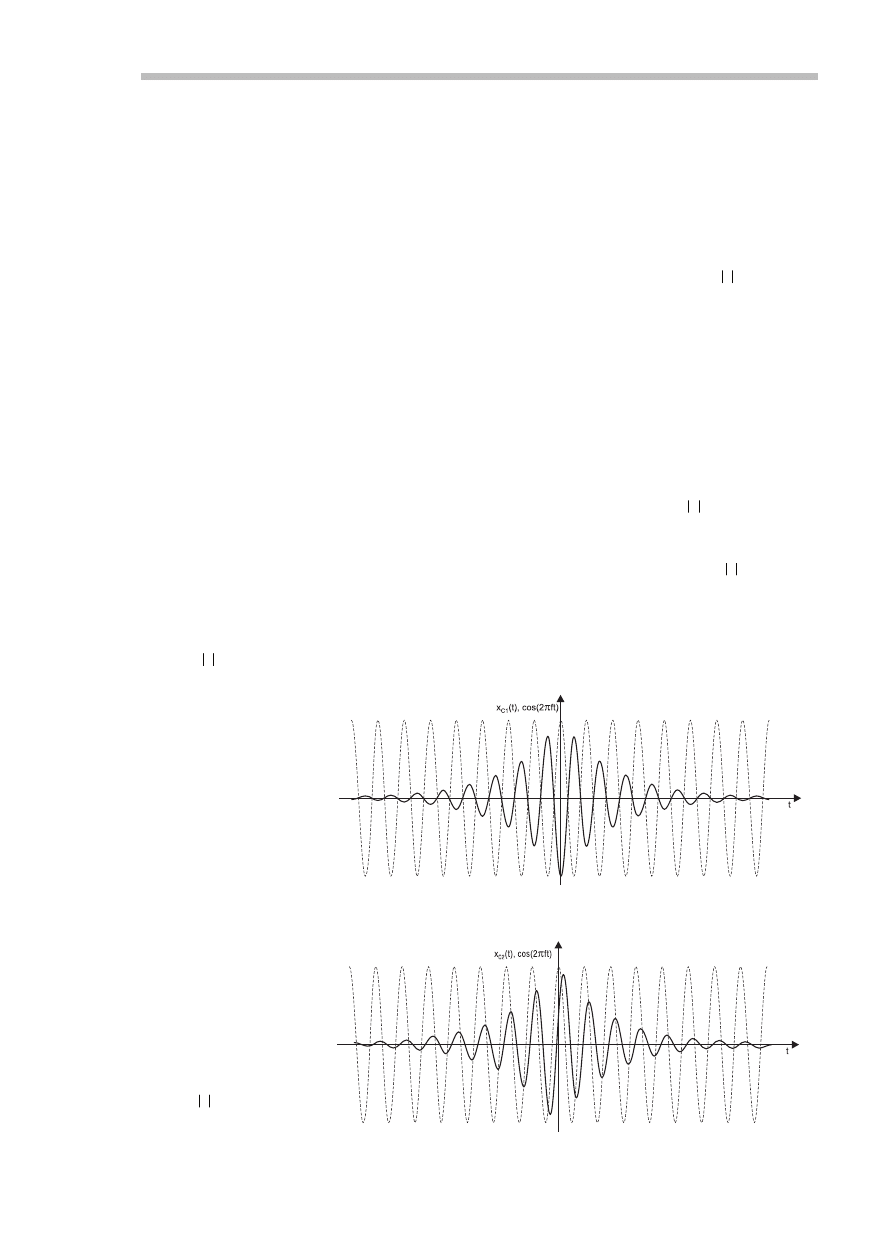
Przeprowadźmy  teraz  kolejny 

eksperyment.  Rozważmy  przypadek, 

gdy  rozpatrywany  sygnał  −  nazwij-

my  go  x

C

2 

(

 

t

 

)  −  będzie  przesunięty 

o 90°.  Taka  sytuacja  jest  przedsta-

wiona  na 

rys.  13.

Przyjrzyjmy  się  dokładnie  do-

wolnemu  pojedynczemu  okresowi. 

W czasie  jednej  ćwiartki  okresu  oby-

dwa  sygnały  zmieniają  się  jednakowo 

(jednocześnie  rosną  lub  maleją),  ale 

już  w kolejnej  zmieniają  się  przeciw-

nie  (tzn.  gdy  jeden  rośnie,  to  drugi 

maleje  i vice  versa).  Odnotowujemy 

więc  zupełny  brak  korelacji  między 

obydwoma  sygnałami.  Dla  pewności 

policzmy  odpowiednią  całkę

(2.13)

Dyskretne  przekształcenie  Fouriera  DFT  (Discrete  Fourier  Transform) 

jest,  obok  procedur  filtracji cyfrowej, jednym z podstawowych,

a zarazem  najbardziej  skutecznych  narzędzi  cyfrowego  przetwarzania 

sygnałów.  Poza  istotnym  znaczeniem  teoretycznym  DFT  odgrywa 

ważną  rolę  w zagadnieniach  związanych  z układowymi  realizacjami 

różnorodnych  algorytmów  przetwarzania  sygnałów.  Wynika  to 

z istnienia  bardzo  wydajnego  algorytmu  obliczania  dyskretnej 

transformaty  Fouriera,  zwanego  szybką  transformatą  Fouriera  FFT 

(Fast  Fourier  Transform).

Rys. 12. Odwrócony w fazie sygnał analizowany (linia ciągła) i sygnał 
cos

 

(2πft

 

) (linia przerywana) – pełna ujemna korelacja

Wynik  obliczeń  potwierdza  nasze 

przewidywania,  ale  i tak  jest  zaskaku-

jący.  Przecież  zawartość  widmowa  sy-

gnału  nie  zmieniła  się!

W tym  miejscu  ujawnia  się  potęga 

rachunku  symbolicznego  i geniusz  Fo-

uriera.  Rozpatrzmy  korelację  sygnału 

x

C

2 

(

 

t

 

)  (przesuniętego  o 90°)  z sygna-

łem  harmonicznym  sin

 

(2πft

 

).  Obydwa 

sygnały  przedstawione  są  na 

rys.  14.

Widzimy  pełną  korelację  obu  sy-

gnałów,  którą  potwierdza  wynik  ob-

liczeń  części  urojonej  transformaty 

Fouriera

 

 

(2.14)

Jak  widać,  nie  ma  korelacji  z sy-

gnałem  cos

 

(2πft

 

),  ale  jest  pełna  ko-

relacja  z sygnałem  sin

 

(2πft

 

).

Na  zakończenie  tej  części  roz-

ważań  rozpatrzymy  przypadek,  gdy 

analizowany  sygnał  jest  przesunięty 

o 45°.  Policzmy  pełną  transformatę 

Fouriera

Rys. 13. Przesunięty o 90°sygnał analizowany (linia ciągła) i sygnał cos

 

(2πft

 

) 

(linia przerywana) – brak korelacji

 

1

Dyskretne przekształcenie Fouriera, cz

��� 3 

JAK MIESI

�C TEMU

Je

�li rozpatrywany sygnał − nazwijmy go x

C1

( t )

− b�dzie odwrócony w fazie, to równie� wyst�pi 

pełna korelacja, w tym sensie, 

�e zmianom sygnału x

C1

( t ) b

�d� towarzyszyły dokładnie przeciwne 

zmiany sygnału harmonicznego cos (2

πft ), wzgl�dem którego wyznaczamy korelacj�, co zilustro-

wano na rys. 12.

Rys. 12. Odwrócony w fazie sygnał analizowany (linia ci

�gła) i sygnał cos (2πft ) (linia przerywana) – 

pełna ujemna korelacja 

Wyliczmy zatem odpowiedni

� całk�

( )

(

)

( )

1

d

2

cos

180

2

cos

e

Re

1

−

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.12) 

Wynik jest zgodny z oczekiwaniami – warto

�� całki jest taka sama, lecz ma przeciwny znak. 

Przeprowad

�my teraz kolejny eksperyment. Rozwa�my przypadek, gdy rozpatrywany sygnał − na-

zwijmy go x

C2

( t )

− b�dzie przesuni�ty o 90°. Taka sytuacja jest przedstawiona na rys. 13.

Rys. 13. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał cos (2πft ) (linia przerywana) – 

brak korelacji 

Przyjrzyjmy si

� dokładnie dowolnemu pojedynczemu okresowi. W czasie jednej �wiartki okresu 

obydwa sygnały zmieniaj

� si� jednakowo (jednocze�nie rosn� lub malej�), ale ju� w kolejnej zmie-

niaj

� si� przeciwnie (tzn. gdy jeden ro�nie, to drugi maleje i vice versa). Odnotowujemy wi�c zu-

pełny brak korelacji mi

�dzy obydwoma sygnałami. Dla pewno�ci policzmy odpowiedni� całk�

( )

(

)

( )

0

d

2

cos

90

2

cos

e

Re

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.13) 

Wynik oblicze

� potwierdza nasze przewidywania, ale i tak jest zaskakuj�cy. Przecie� zawarto��

widmowa sygnału nie zmieniła si

�!

W tym miejscu ujawnia si

� pot�ga rachunku symbolicznego i geniusz Fouriera. Rozpatrzmy korela-

cj

� sygnału x

C2

( t ) (przesuni

�tego o 90°) z sygnałem harmonicznym sin (2πft ). Obydwa sygnały 

przedstawione s

� na rys. 14.

Rys. 14. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał sin (2πft ) (linia przerywana) – 

pełna korelacja 

Widzimy pełn

� korelacj� obu sygnałów, któr� potwierdza wynik oblicze� cz��ci urojonej transfor-

maty Fouriera 

( )

(

) ( )

1

d

2

sin

90

2

cos

e

Im

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.14) 

Jak wida

�, nie ma korelacji z sygnałem cos (2πft ), ale jest pełna korelacja z sygnałem sin (2πft ).

Na zako

�czenie tej cz��ci rozwa�a� przeanalizujemy przypadek, gdy analizowany sygnał jest prze-

suni

�ty o 45°. Policzmy pełn� transformat� Fouriera 

 

1

Dyskretne przekształcenie Fouriera, cz

��� 3 

JAK MIESI

�C TEMU

Je

�li rozpatrywany sygnał − nazwijmy go x

C1

( t )

− b�dzie odwrócony w fazie, to równie� wyst�pi 

pełna korelacja, w tym sensie, 

�e zmianom sygnału x

C1

( t ) b

�d� towarzyszyły dokładnie przeciwne 

zmiany sygnału harmonicznego cos (2

πft ), wzgl�dem którego wyznaczamy korelacj�, co zilustro-

wano na rys. 12.

Rys. 12. Odwrócony w fazie sygnał analizowany (linia ci

�gła) i sygnał cos (2πft ) (linia przerywana) – 

pełna ujemna korelacja 

Wyliczmy zatem odpowiedni

� całk�

( )

(

)

( )

1

d

2

cos

180

2

cos

e

Re

1

−

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.12) 

Wynik jest zgodny z oczekiwaniami – warto

�� całki jest taka sama, lecz ma przeciwny znak. 

Przeprowad

�my teraz kolejny eksperyment. Rozwa�my przypadek, gdy rozpatrywany sygnał − na-

zwijmy go x

C2

( t )

− b�dzie przesuni�ty o 90°. Taka sytuacja jest przedstawiona na rys. 13.

Rys. 13. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał cos (2πft ) (linia przerywana) – 

brak korelacji 

Przyjrzyjmy si

� dokładnie dowolnemu pojedynczemu okresowi. W czasie jednej �wiartki okresu 

obydwa sygnały zmieniaj

� si� jednakowo (jednocze�nie rosn� lub malej�), ale ju� w kolejnej zmie-

niaj

� si� przeciwnie (tzn. gdy jeden ro�nie, to drugi maleje i vice versa). Odnotowujemy wi�c zu-

pełny brak korelacji mi

�dzy obydwoma sygnałami. Dla pewno�ci policzmy odpowiedni� całk�

( )

(

)

( )

0

d

2

cos

90

2

cos

e

Re

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.13) 

Wynik oblicze

� potwierdza nasze przewidywania, ale i tak jest zaskakuj�cy. Przecie� zawarto��

widmowa sygnału nie zmieniła si

�!

W tym miejscu ujawnia si

� pot�ga rachunku symbolicznego i geniusz Fouriera. Rozpatrzmy korela-

cj

� sygnału x

C2

( t ) (przesuni

�tego o 90°) z sygnałem harmonicznym sin (2πft ). Obydwa sygnały 

przedstawione s

� na rys. 14.

Rys. 14. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał sin (2πft ) (linia przerywana) – 

pełna korelacja 

Widzimy pełn

� korelacj� obu sygnałów, któr� potwierdza wynik oblicze� cz��ci urojonej transfor-

maty Fouriera 

( )

(

) ( )

1

d

2

sin

90

2

cos

e

Im

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.14) 

Jak wida

�, nie ma korelacji z sygnałem cos (2πft ), ale jest pełna korelacja z sygnałem sin (2πft ).

Na zako

�czenie tej cz��ci rozwa�a� przeanalizujemy przypadek, gdy analizowany sygnał jest prze-

suni

�ty o 45°. Policzmy pełn� transformat� Fouriera 

 

1

Dyskretne przekształcenie Fouriera, cz

��� 3 

JAK MIESI

�C TEMU

Je

�li rozpatrywany sygnał − nazwijmy go x

C1

( t )

− b�dzie odwrócony w fazie, to równie� wyst�pi 

pełna korelacja, w tym sensie, 

�e zmianom sygnału x

C1

( t ) b

�d� towarzyszyły dokładnie przeciwne 

zmiany sygnału harmonicznego cos (2

πft ), wzgl�dem którego wyznaczamy korelacj�, co zilustro-

wano na rys. 12.

Rys. 12. Odwrócony w fazie sygnał analizowany (linia ci

�gła) i sygnał cos (2πft ) (linia przerywana) – 

pełna ujemna korelacja 

Wyliczmy zatem odpowiedni

� całk�

( )

(

)

( )

1

d

2

cos

180

2

cos

e

Re

1

−

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.12) 

Wynik jest zgodny z oczekiwaniami – warto

�� całki jest taka sama, lecz ma przeciwny znak. 

Przeprowad

�my teraz kolejny eksperyment. Rozwa�my przypadek, gdy rozpatrywany sygnał − na-

zwijmy go x

C2

( t )

− b�dzie przesuni�ty o 90°. Taka sytuacja jest przedstawiona na rys. 13.

Rys. 13. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał cos (2πft ) (linia przerywana) – 

brak korelacji 

Przyjrzyjmy si

� dokładnie dowolnemu pojedynczemu okresowi. W czasie jednej �wiartki okresu 

obydwa sygnały zmieniaj

� si� jednakowo (jednocze�nie rosn� lub malej�), ale ju� w kolejnej zmie-

niaj

� si� przeciwnie (tzn. gdy jeden ro�nie, to drugi maleje i vice versa). Odnotowujemy wi�c zu-

pełny brak korelacji mi

�dzy obydwoma sygnałami. Dla pewno�ci policzmy odpowiedni� całk�

( )

(

)

( )

0

d

2

cos

90

2

cos

e

Re

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.13) 

Wynik oblicze

� potwierdza nasze przewidywania, ale i tak jest zaskakuj�cy. Przecie� zawarto��

widmowa sygnału nie zmieniła si

�!

W tym miejscu ujawnia si

� pot�ga rachunku symbolicznego i geniusz Fouriera. Rozpatrzmy korela-

cj

� sygnału x

C2

( t ) (przesuni

�tego o 90°) z sygnałem harmonicznym sin (2πft ). Obydwa sygnały 

przedstawione s

� na rys. 14.

Rys. 14. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał sin (2πft ) (linia przerywana) – 

pełna korelacja 

Widzimy pełn

� korelacj� obu sygnałów, któr� potwierdza wynik oblicze� cz��ci urojonej transfor-

maty Fouriera 

( )

(

) ( )

1

d

2

sin

90

2

cos

e

Im

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.14) 

Jak wida

�, nie ma korelacji z sygnałem cos (2πft ), ale jest pełna korelacja z sygnałem sin (2πft ).

Na zako

�czenie tej cz��ci rozwa�a� przeanalizujemy przypadek, gdy analizowany sygnał jest prze-

suni

�ty o 45°. Policzmy pełn� transformat� Fouriera 

 

1

Dyskretne przekształcenie Fouriera, cz

��� 3 

JAK MIESI

�C TEMU

Je

�li rozpatrywany sygnał − nazwijmy go x

C1

( t )

− b�dzie odwrócony w fazie, to równie� wyst�pi 

pełna korelacja, w tym sensie, 

�e zmianom sygnału x

C1

( t ) b

�d� towarzyszyły dokładnie przeciwne 

zmiany sygnału harmonicznego cos (2

πft ), wzgl�dem którego wyznaczamy korelacj�, co zilustro-

wano na rys. 12.

Rys. 12. Odwrócony w fazie sygnał analizowany (linia ci

�gła) i sygnał cos (2πft ) (linia przerywana) – 

pełna ujemna korelacja 

Wyliczmy zatem odpowiedni

� całk�

( )

(

)

( )

1

d

2

cos

180

2

cos

e

Re

1

−

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.12) 

Wynik jest zgodny z oczekiwaniami – warto

�� całki jest taka sama, lecz ma przeciwny znak. 

Przeprowad

�my teraz kolejny eksperyment. Rozwa�my przypadek, gdy rozpatrywany sygnał − na-

zwijmy go x

C2

( t )

− b�dzie przesuni�ty o 90°. Taka sytuacja jest przedstawiona na rys. 13.

Rys. 13. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał cos (2πft ) (linia przerywana) – 

brak korelacji 

Przyjrzyjmy si

� dokładnie dowolnemu pojedynczemu okresowi. W czasie jednej �wiartki okresu 

obydwa sygnały zmieniaj

� si� jednakowo (jednocze�nie rosn� lub malej�), ale ju� w kolejnej zmie-

niaj

� si� przeciwnie (tzn. gdy jeden ro�nie, to drugi maleje i vice versa). Odnotowujemy wi�c zu-

pełny brak korelacji mi

�dzy obydwoma sygnałami. Dla pewno�ci policzmy odpowiedni� całk�

( )

(

)

( )

0

d

2

cos

90

2

cos

e

Re

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.13) 

Wynik oblicze

� potwierdza nasze przewidywania, ale i tak jest zaskakuj�cy. Przecie� zawarto��

widmowa sygnału nie zmieniła si

�!

W tym miejscu ujawnia si

� pot�ga rachunku symbolicznego i geniusz Fouriera. Rozpatrzmy korela-

cj

� sygnału x

C2

( t ) (przesuni

�tego o 90°) z sygnałem harmonicznym sin (2πft ). Obydwa sygnały 

przedstawione s

� na rys. 14.

Rys. 14. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał sin (2πft ) (linia przerywana) – 

pełna korelacja 

Widzimy pełn

� korelacj� obu sygnałów, któr� potwierdza wynik oblicze� cz��ci urojonej transfor-

maty Fouriera 

( )

(

) ( )

1

d

2

sin

90

2

cos

e

Im

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.14) 

Jak wida

�, nie ma korelacji z sygnałem cos (2πft ), ale jest pełna korelacja z sygnałem sin (2πft ).

Na zako

�czenie tej cz��ci rozwa�a� przeanalizujemy przypadek, gdy analizowany sygnał jest prze-

suni

�ty o 45°. Policzmy pełn� transformat� Fouriera 

 

1

Dyskretne przekształcenie Fouriera, cz

��� 3 

JAK MIESI

�C TEMU

Je

�li rozpatrywany sygnał − nazwijmy go x

C1

( t )

− b�dzie odwrócony w fazie, to równie� wyst�pi 

pełna korelacja, w tym sensie, 

�e zmianom sygnału x

C1

( t ) b

�d� towarzyszyły dokładnie przeciwne 

zmiany sygnału harmonicznego cos (2

πft ), wzgl�dem którego wyznaczamy korelacj�, co zilustro-

wano na rys. 12.

Rys. 12. Odwrócony w fazie sygnał analizowany (linia ci

�gła) i sygnał cos (2πft ) (linia przerywana) – 

pełna ujemna korelacja 

Wyliczmy zatem odpowiedni

� całk�

( )

(

)

( )

1

d

2

cos

180

2

cos

e

Re

1

−

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.12) 

Wynik jest zgodny z oczekiwaniami – warto

�� całki jest taka sama, lecz ma przeciwny znak. 

Przeprowad

�my teraz kolejny eksperyment. Rozwa�my przypadek, gdy rozpatrywany sygnał − na-

zwijmy go x

C2

( t )

− b�dzie przesuni�ty o 90°. Taka sytuacja jest przedstawiona na rys. 13.

Rys. 13. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał cos (2πft ) (linia przerywana) – 

brak korelacji 

Przyjrzyjmy si

� dokładnie dowolnemu pojedynczemu okresowi. W czasie jednej �wiartki okresu 

obydwa sygnały zmieniaj

� si� jednakowo (jednocze�nie rosn� lub malej�), ale ju� w kolejnej zmie-

niaj

� si� przeciwnie (tzn. gdy jeden ro�nie, to drugi maleje i vice versa). Odnotowujemy wi�c zu-

pełny brak korelacji mi

�dzy obydwoma sygnałami. Dla pewno�ci policzmy odpowiedni� całk�

( )

(

)

( )

0

d

2

cos

90

2

cos

e

Re

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.13) 

Wynik oblicze

� potwierdza nasze przewidywania, ale i tak jest zaskakuj�cy. Przecie� zawarto��

widmowa sygnału nie zmieniła si

�!

W tym miejscu ujawnia si

� pot�ga rachunku symbolicznego i geniusz Fouriera. Rozpatrzmy korela-

cj

� sygnału x

C2

( t ) (przesuni

�tego o 90°) z sygnałem harmonicznym sin (2πft ). Obydwa sygnały 

przedstawione s

� na rys. 14.

Rys. 14. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał sin (2πft ) (linia przerywana) – 

pełna korelacja 

Widzimy pełn

� korelacj� obu sygnałów, któr� potwierdza wynik oblicze� cz��ci urojonej transfor-

maty Fouriera 

( )

(

) ( )

1

d

2

sin

90

2

cos

e

Im

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.14) 

Jak wida

�, nie ma korelacji z sygnałem cos (2πft ), ale jest pełna korelacja z sygnałem sin (2πft ).

Na zako

�czenie tej cz��ci rozwa�a� przeanalizujemy przypadek, gdy analizowany sygnał jest prze-

suni

�ty o 45°. Policzmy pełn� transformat� Fouriera 

 

1

Dyskretne przekształcenie Fouriera, cz

��� 3 

JAK MIESI

�C TEMU

Je

�li rozpatrywany sygnał − nazwijmy go x

C1

( t )

− b�dzie odwrócony w fazie, to równie� wyst�pi 

pełna korelacja, w tym sensie, 

�e zmianom sygnału x

C1

( t ) b

�d� towarzyszyły dokładnie przeciwne 

zmiany sygnału harmonicznego cos (2

πft ), wzgl�dem którego wyznaczamy korelacj�, co zilustro-

wano na rys. 12.

Rys. 12. Odwrócony w fazie sygnał analizowany (linia ci

�gła) i sygnał cos (2πft ) (linia przerywana) – 

pełna ujemna korelacja 

Wyliczmy zatem odpowiedni

� całk�

( )

(

)

( )

1

d

2

cos

180

2

cos

e

Re

1

−

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.12) 

Wynik jest zgodny z oczekiwaniami – warto

�� całki jest taka sama, lecz ma przeciwny znak. 

Przeprowad

�my teraz kolejny eksperyment. Rozwa�my przypadek, gdy rozpatrywany sygnał − na-

zwijmy go x

C2

( t )

− b�dzie przesuni�ty o 90°. Taka sytuacja jest przedstawiona na rys. 13.

Rys. 13. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał cos (2πft ) (linia przerywana) – 

brak korelacji 

Przyjrzyjmy si

� dokładnie dowolnemu pojedynczemu okresowi. W czasie jednej �wiartki okresu 

obydwa sygnały zmieniaj

� si� jednakowo (jednocze�nie rosn� lub malej�), ale ju� w kolejnej zmie-

niaj

� si� przeciwnie (tzn. gdy jeden ro�nie, to drugi maleje i vice versa). Odnotowujemy wi�c zu-

pełny brak korelacji mi

�dzy obydwoma sygnałami. Dla pewno�ci policzmy odpowiedni� całk�

( )

(

)

( )

0

d

2

cos

90

2

cos

e

Re

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.13) 

Wynik oblicze

� potwierdza nasze przewidywania, ale i tak jest zaskakuj�cy. Przecie� zawarto��

widmowa sygnału nie zmieniła si

�!

W tym miejscu ujawnia si

� pot�ga rachunku symbolicznego i geniusz Fouriera. Rozpatrzmy korela-

cj

� sygnału x

C2

( t ) (przesuni

�tego o 90°) z sygnałem harmonicznym sin (2πft ). Obydwa sygnały 

przedstawione s

� na rys. 14.

Rys. 14. Przesuni

�ty o 90°sygnał analizowany (linia ci�gła) i sygnał sin (2πft ) (linia przerywana) – 

pełna korelacja 

Widzimy pełn

� korelacj� obu sygnałów, któr� potwierdza wynik oblicze� cz��ci urojonej transfor-

maty Fouriera 

( )

(

) ( )

1

d

2

sin

90

2

cos

e

Im

2

=

�

�

�

π

⋅

°

−

π

=

�

�

�

�

�

�

∞

∞

−

−

t

ft

ft

f

X

t

C

 

(2.14) 

Jak wida

�, nie ma korelacji z sygnałem cos (2πft ), ale jest pełna korelacja z sygnałem sin (2πft ).

Na zako

�czenie tej cz��ci rozwa�a� przeanalizujemy przypadek, gdy analizowany sygnał jest prze-

suni

�ty o 45°. Policzmy pełn� transformat� Fouriera 

 

2

( )

(

) (

)

(

) (

)

°

−

∞

∞

−

−

∞

∞

−

−

=

−

=

=

�

�

�

π

°

−

π

−

�

�

�

π

°

−

π

=

45

j

3

e

1

707

,

0

j

707

,

0

d

2

sin

45

2

cos

e

j

d

2

cos

45

2

cos

e

t

ft

ft

t

ft

ft

f

X

t

t

C

(2.15) 

Wynik oblicze

� wskazuje, �e moduł transformaty jest równy jedno�ci, a ró�ny od zera wykładnik 

informuje o przesuni

�ciu fazowym sygnału poddanego transformacji wzgl�dem sygnału odniesienia 

cos (2

πft ).

Na podstawie pokazanych przypadków, wykorzystuj

�c odrobin� dedukcji, dochodzimy do wniosku, 

�e je�li kształt sygnału nie zmienia si�, to niezale�nie od jego przesuni�cia fazowego, moduł trans-

formaty Fouriera jest zawsze jednakowy, a zmienia si

� jedynie jej faza, okre�laj�c poło�enie sygna-

łu wzgl

�dem składowej kosinusoidalnej. 

Je

�li analizowany sygnał b�dzie sum� kilku składowych harmonicznych, to moduł transformaty 

Fouriera b

�dzie osi�gał lokalnie maksymalne warto�ci dla cz�stotliwo�ci równych cz�stotliwo�ciom 

tych składowych. Wynika to z faktu, 

�e tylko dla tych składowych istnieje korelacja mi�dzy anali-

zowanym sygnałem i odpowiednim harmonicznym sygnałem odniesienia. 

Przekształcenie Fouriera sygnału dyskretnego 
Jak mogli

�my si� przekona�, transformata Fouriera sygnału ci�głego ma bardzo klarown� i intu-

icyjn

� interpretacj� fizyczn�. Obecnie rozpatrzymy proces transformacji Fourierowskiej sygnału o 

czasie dyskretnym. Na pocz

�tku usystematyzujemy poj�cia zwi�zane z sygnałami ci�głymi, dys-

kretnymi i cyfrowymi oraz rzucimy nieco 

�wiatła na sam proces próbkowania. 

W wyniku próbkowania sygnałów ci

�głych otrzymujemy sygnały o czasie dyskretnym nazywane w 

literaturze polskiej sygnałami dyskretnymi. Z kolei sygnał dyskretny poddany kwantyzacji warto

�ci

chwilowej i zapisowi w postaci ci

�gu liczb nosi nazw� sygnału cyfrowego. Sygnał cyfrowy jest 

wi

�c sygnałem dyskretnym zarówno w czasie, jak i − ze wzgl�du na sko�czon� ilo�� poziomów 

kwantowania 

− w warto�ci. Sygnał cyfrowy, b�d�cy z programowego punktu widzenia wektorem

1

,

mo

�e by� bezpo�rednio poddawany procedurom cyfrowego przetwarzania sygnałów.  

Proces próbkowania polega na pomiarze warto

�ci sygnału w �ci�le okre�lonych momentach czaso-

wych. W najprostszym przypadku mamy do czynienia z próbkowaniem równomiernym [3, 4], któ-
rego zasady s

� okre�lone przez twierdzenie Kotielnikowa − Shannona. Proces próbkowania ma z 

reguły miejsce w wi

�kszo�ci współczesnych przyrz�dów pomiarowych oraz w programach do ana-

lizy układów elektronicznych.  
W pierwszym przypadku próbkowanie jest realizowane w celu pó

�niejszego zastosowania wybra-

nych algorytmów CPS oraz archiwizacji danych pomiarowych. W drugim 

− „próbkowanie” odby-

wa si

� „przypadkiem” w wyniku realizacji procedur całkowania numerycznego. Słowo próbkowa-

nie zostało wzi

�te w cudzysłów, gdy� nie mamy tu do czynienia z pomiarem, lecz predykcj� warto-

�ci przebiegu w wybranych momentach czasowych. 

W przeciwie

�stwie do przyrz�dów pomiarowych, programy realizuj�ce analiz� czasow� układów 

elektronicznych z reguły nie „próbkuj

�” sygnału równomiernie, ale praktycznie, za pomoc� proce-

dur interpolacji wielomianowej (najcz

��ciej liniowej), daj� w efekcie ko�cowym sygnał spróbko-

wany równomiernie [2]. Z tego powodu dalsze rozwa

�ania ograniczymy do przypadku sygnału 

dyskretnego z jednakowym odst

�pem czasowym mi�dzy s�siednimi próbkami.  

Na samym pocz

�tku rozwa�a� w �wiecie sygnałów dyskretnych pojawia si� pytanie – Jak taki sy-

gnał zapisa

� analitycznie? Z pomoc� przychodzi nam teoria dystrybucji z tzw. delt� Diraca δ(t). 

Nie wgł

�biaj�c si� w zawiło�ci matematyczne, przyjmijmy do wiadomo�ci, �e delta Diraca ma nie-

sko

�czenie du�� warto�� w momencie t = 0, a w pozostałym czasie jest równa zeru. Ponadto całka 

1

 Czyli uporz

�dkowanym ci�giem liczb o wspólnej nazwie. 

 

2

( )

(

) (

)

(

) (

)

°

−

∞

∞

−

−

∞

∞

−

−

=

−

=

=

�

�

�

π

°

−

π

−

�

�

�

π

°

−

π

=

45

j

3

e

1

707

,

0

j

707

,

0

d

2

sin

45

2

cos

e

j

d

2

cos

45

2

cos

e

t

ft

ft

t

ft

ft

f

X

t

t

C

(2.15) 

Wynik oblicze

� wskazuje, �e moduł transformaty jest równy jedno�ci, a ró�ny od zera wykładnik 

informuje o przesuni

�ciu fazowym sygnału poddanego transformacji wzgl�dem sygnału odniesienia 

cos (2

πft ).

Na podstawie pokazanych przypadków, wykorzystuj

�c odrobin� dedukcji, dochodzimy do wniosku, 

�e je�li kształt sygnału nie zmienia si�, to niezale�nie od jego przesuni�cia fazowego, moduł trans-

formaty Fouriera jest zawsze jednakowy, a zmienia si

� jedynie jej faza, okre�laj�c poło�enie sygna-

łu wzgl

�dem składowej kosinusoidalnej. 

Je

�li analizowany sygnał b�dzie sum� kilku składowych harmonicznych, to moduł transformaty 

Fouriera b

�dzie osi�gał lokalnie maksymalne warto�ci dla cz�stotliwo�ci równych cz�stotliwo�ciom 

tych składowych. Wynika to z faktu, 

�e tylko dla tych składowych istnieje korelacja mi�dzy anali-

zowanym sygnałem i odpowiednim harmonicznym sygnałem odniesienia. 

Przekształcenie Fouriera sygnału dyskretnego 
Jak mogli

�my si� przekona�, transformata Fouriera sygnału ci�głego ma bardzo klarown� i intu-

icyjn

� interpretacj� fizyczn�. Obecnie rozpatrzymy proces transformacji Fourierowskiej sygnału o 

czasie dyskretnym. Na pocz

�tku usystematyzujemy poj�cia zwi�zane z sygnałami ci�głymi, dys-

kretnymi i cyfrowymi oraz rzucimy nieco 

�wiatła na sam proces próbkowania. 

W wyniku próbkowania sygnałów ci

�głych otrzymujemy sygnały o czasie dyskretnym nazywane w 

literaturze polskiej sygnałami dyskretnymi. Z kolei sygnał dyskretny poddany kwantyzacji warto

�ci

chwilowej i zapisowi w postaci ci

�gu liczb nosi nazw� sygnału cyfrowego. Sygnał cyfrowy jest 

wi

�c sygnałem dyskretnym zarówno w czasie, jak i − ze wzgl�du na sko�czon� ilo�� poziomów 

kwantowania 

− w warto�ci. Sygnał cyfrowy, b�d�cy z programowego punktu widzenia wektorem

1

,

mo

�e by� bezpo�rednio poddawany procedurom cyfrowego przetwarzania sygnałów.  

Proces próbkowania polega na pomiarze warto

�ci sygnału w �ci�le okre�lonych momentach czaso-

wych. W najprostszym przypadku mamy do czynienia z próbkowaniem równomiernym [3, 4], któ-
rego zasady s

� okre�lone przez twierdzenie Kotielnikowa − Shannona. Proces próbkowania ma z 

reguły miejsce w wi

�kszo�ci współczesnych przyrz�dów pomiarowych oraz w programach do ana-

lizy układów elektronicznych.  
W pierwszym przypadku próbkowanie jest realizowane w celu pó

�niejszego zastosowania wybra-

nych algorytmów CPS oraz archiwizacji danych pomiarowych. W drugim 

− „próbkowanie” odby-

wa si

� „przypadkiem” w wyniku realizacji procedur całkowania numerycznego. Słowo próbkowa-

nie zostało wzi

�te w cudzysłów, gdy� nie mamy tu do czynienia z pomiarem, lecz predykcj� warto-

�ci przebiegu w wybranych momentach czasowych. 

W przeciwie

�stwie do przyrz�dów pomiarowych, programy realizuj�ce analiz� czasow� układów 

elektronicznych z reguły nie „próbkuj

�” sygnału równomiernie, ale praktycznie, za pomoc� proce-

dur interpolacji wielomianowej (najcz

��ciej liniowej), daj� w efekcie ko�cowym sygnał spróbko-

wany równomiernie [2]. Z tego powodu dalsze rozwa

�ania ograniczymy do przypadku sygnału 

dyskretnego z jednakowym odst

�pem czasowym mi�dzy s�siednimi próbkami.  

Na samym pocz

�tku rozwa�a� w �wiecie sygnałów dyskretnych pojawia si� pytanie – Jak taki sy-

gnał zapisa

� analitycznie? Z pomoc� przychodzi nam teoria dystrybucji z tzw. delt� Diraca δ(t). 

Nie wgł

�biaj�c si� w zawiło�ci matematyczne, przyjmijmy do wiadomo�ci, �e delta Diraca ma nie-

sko

�czenie du�� warto�� w momencie t = 0, a w pozostałym czasie jest równa zeru. Ponadto całka 

1

 Czyli uporz

�dkowanym ci�giem liczb o wspólnej nazwie. 

 

2

( )

(

) (

)

(

) (

)

°

−

∞

∞

−

−

∞

∞

−

−

=

−

=

=

�

�

�

π

°

−

π

−

�

�

�

π

°

−

π

=

45

j

3

e

1

707

,

0

j

707

,

0

d

2

sin

45

2

cos

e

j

d

2

cos

45

2

cos

e

t

ft

ft

t

ft

ft

f

X

t

t

C

(2.15) 

Wynik oblicze

� wskazuje, �e moduł transformaty jest równy jedno�ci, a ró�ny od zera wykładnik 

informuje o przesuni

�ciu fazowym sygnału poddanego transformacji wzgl�dem sygnału odniesienia 

cos (2

πft ).

Na podstawie pokazanych przypadków, wykorzystuj

�c odrobin� dedukcji, dochodzimy do wniosku, 

�e je�li kształt sygnału nie zmienia si�, to niezale�nie od jego przesuni�cia fazowego, moduł trans-

formaty Fouriera jest zawsze jednakowy, a zmienia si

� jedynie jej faza, okre�laj�c poło�enie sygna-

łu wzgl

�dem składowej kosinusoidalnej. 

Je

�li analizowany sygnał b�dzie sum� kilku składowych harmonicznych, to moduł transformaty 

Fouriera b

�dzie osi�gał lokalnie maksymalne warto�ci dla cz�stotliwo�ci równych cz�stotliwo�ciom 

tych składowych. Wynika to z faktu, 

�e tylko dla tych składowych istnieje korelacja mi�dzy anali-

zowanym sygnałem i odpowiednim harmonicznym sygnałem odniesienia. 

Przekształcenie Fouriera sygnału dyskretnego 
Jak mogli

�my si� przekona�, transformata Fouriera sygnału ci�głego ma bardzo klarown� i intu-

icyjn

� interpretacj� fizyczn�. Obecnie rozpatrzymy proces transformacji Fourierowskiej sygnału o 

czasie dyskretnym. Na pocz

�tku usystematyzujemy poj�cia zwi�zane z sygnałami ci�głymi, dys-

kretnymi i cyfrowymi oraz rzucimy nieco 

�wiatła na sam proces próbkowania. 

W wyniku próbkowania sygnałów ci

�głych otrzymujemy sygnały o czasie dyskretnym nazywane w 

literaturze polskiej sygnałami dyskretnymi. Z kolei sygnał dyskretny poddany kwantyzacji warto

�ci

chwilowej i zapisowi w postaci ci

�gu liczb nosi nazw� sygnału cyfrowego. Sygnał cyfrowy jest 

wi

�c sygnałem dyskretnym zarówno w czasie, jak i − ze wzgl�du na sko�czon� ilo�� poziomów 

kwantowania 

− w warto�ci. Sygnał cyfrowy, b�d�cy z programowego punktu widzenia wektorem

1

,

mo

�e by� bezpo�rednio poddawany procedurom cyfrowego przetwarzania sygnałów.  

Proces próbkowania polega na pomiarze warto

�ci sygnału w �ci�le okre�lonych momentach czaso-

wych. W najprostszym przypadku mamy do czynienia z próbkowaniem równomiernym [3, 4], któ-
rego zasady s

� okre�lone przez twierdzenie Kotielnikowa − Shannona. Proces próbkowania ma z 

reguły miejsce w wi

�kszo�ci współczesnych przyrz�dów pomiarowych oraz w programach do ana-

lizy układów elektronicznych.  
W pierwszym przypadku próbkowanie jest realizowane w celu pó

�niejszego zastosowania wybra-

nych algorytmów CPS oraz archiwizacji danych pomiarowych. W drugim 

− „próbkowanie” odby-

wa si

� „przypadkiem” w wyniku realizacji procedur całkowania numerycznego. Słowo próbkowa-

nie zostało wzi

�te w cudzysłów, gdy� nie mamy tu do czynienia z pomiarem, lecz predykcj� warto-

�ci przebiegu w wybranych momentach czasowych. 

W przeciwie

�stwie do przyrz�dów pomiarowych, programy realizuj�ce analiz� czasow� układów 

elektronicznych z reguły nie „próbkuj

�” sygnału równomiernie, ale praktycznie, za pomoc� proce-

dur interpolacji wielomianowej (najcz

��ciej liniowej), daj� w efekcie ko�cowym sygnał spróbko-

wany równomiernie [2]. Z tego powodu dalsze rozwa

�ania ograniczymy do przypadku sygnału 

dyskretnego z jednakowym odst

�pem czasowym mi�dzy s�siednimi próbkami.  

Na samym pocz

�tku rozwa�a� w �wiecie sygnałów dyskretnych pojawia si� pytanie – Jak taki sy-

gnał zapisa

� analitycznie? Z pomoc� przychodzi nam teoria dystrybucji z tzw. delt� Diraca δ(t). 

Nie wgł

�biaj�c si� w zawiło�ci matematyczne, przyjmijmy do wiadomo�ci, �e delta Diraca ma nie-

sko

�czenie du�� warto�� w momencie t = 0, a w pozostałym czasie jest równa zeru. Ponadto całka 

1

 Czyli uporz

�dkowanym ci�giem liczb o wspólnej nazwie. 

 

2

( )

(

) (

)

(

) (

)

°

−

∞

∞

−

−

∞

∞

−

−

=

−

=

=

�

�

�

π

°

−

π

−

�

�

�

π

°

−

π

=

45

j

3

e

1

707

,

0

j

707

,

0

d

2

sin

45

2

cos

e

j

d

2

cos

45

2

cos

e

t

ft

ft

t

ft

ft

f

X

t

t

C

(2.15) 

Wynik oblicze

� wskazuje, �e moduł transformaty jest równy jedno�ci, a ró�ny od zera wykładnik 

informuje o przesuni

�ciu fazowym sygnału poddanego transformacji wzgl�dem sygnału odniesienia 

cos (2

πft ).

Na podstawie pokazanych przypadków, wykorzystuj

�c odrobin� dedukcji, dochodzimy do wniosku, 

�e je�li kształt sygnału nie zmienia si�, to niezale�nie od jego przesuni�cia fazowego, moduł trans-

formaty Fouriera jest zawsze jednakowy, a zmienia si

� jedynie jej faza, okre�laj�c poło�enie sygna-

łu wzgl

�dem składowej kosinusoidalnej. 

Je

�li analizowany sygnał b�dzie sum� kilku składowych harmonicznych, to moduł transformaty 

Fouriera b

�dzie osi�gał lokalnie maksymalne warto�ci dla cz�stotliwo�ci równych cz�stotliwo�ciom 

tych składowych. Wynika to z faktu, 

�e tylko dla tych składowych istnieje korelacja mi�dzy anali-

zowanym sygnałem i odpowiednim harmonicznym sygnałem odniesienia. 

Przekształcenie Fouriera sygnału dyskretnego 
Jak mogli

�my si� przekona�, transformata Fouriera sygnału ci�głego ma bardzo klarown� i intu-

icyjn

� interpretacj� fizyczn�. Obecnie rozpatrzymy proces transformacji Fourierowskiej sygnału o 

czasie dyskretnym. Na pocz

�tku usystematyzujemy poj�cia zwi�zane z sygnałami ci�głymi, dys-

kretnymi i cyfrowymi oraz rzucimy nieco 

�wiatła na sam proces próbkowania. 

W wyniku próbkowania sygnałów ci

�głych otrzymujemy sygnały o czasie dyskretnym nazywane w 

literaturze polskiej sygnałami dyskretnymi. Z kolei sygnał dyskretny poddany kwantyzacji warto

�ci

chwilowej i zapisowi w postaci ci

�gu liczb nosi nazw� sygnału cyfrowego. Sygnał cyfrowy jest 

wi

�c sygnałem dyskretnym zarówno w czasie, jak i − ze wzgl�du na sko�czon� ilo�� poziomów 

kwantowania 

− w warto�ci. Sygnał cyfrowy, b�d�cy z programowego punktu widzenia wektorem

1

,

mo

�e by� bezpo�rednio poddawany procedurom cyfrowego przetwarzania sygnałów.  

Proces próbkowania polega na pomiarze warto

�ci sygnału w �ci�le okre�lonych momentach czaso-

wych. W najprostszym przypadku mamy do czynienia z próbkowaniem równomiernym [3, 4], któ-
rego zasady s

� okre�lone przez twierdzenie Kotielnikowa − Shannona. Proces próbkowania ma z 

reguły miejsce w wi

�kszo�ci współczesnych przyrz�dów pomiarowych oraz w programach do ana-

lizy układów elektronicznych.  
W pierwszym przypadku próbkowanie jest realizowane w celu pó

�niejszego zastosowania wybra-

nych algorytmów CPS oraz archiwizacji danych pomiarowych. W drugim 

− „próbkowanie” odby-

wa si

� „przypadkiem” w wyniku realizacji procedur całkowania numerycznego. Słowo próbkowa-

nie zostało wzi

�te w cudzysłów, gdy� nie mamy tu do czynienia z pomiarem, lecz predykcj� warto-

�ci przebiegu w wybranych momentach czasowych. 

W przeciwie

�stwie do przyrz�dów pomiarowych, programy realizuj�ce analiz� czasow� układów 

elektronicznych z reguły nie „próbkuj

�” sygnału równomiernie, ale praktycznie, za pomoc� proce-

dur interpolacji wielomianowej (najcz

��ciej liniowej), daj� w efekcie ko�cowym sygnał spróbko-

wany równomiernie [2]. Z tego powodu dalsze rozwa

�ania ograniczymy do przypadku sygnału 

dyskretnego z jednakowym odst

�pem czasowym mi�dzy s�siednimi próbkami.  

Na samym pocz

�tku rozwa�a� w �wiecie sygnałów dyskretnych pojawia si� pytanie – Jak taki sy-

gnał zapisa

� analitycznie? Z pomoc� przychodzi nam teoria dystrybucji z tzw. delt� Diraca δ(t). 

Nie wgł

�biaj�c si� w zawiło�ci matematyczne, przyjmijmy do wiadomo�ci, �e delta Diraca ma nie-

sko

�czenie du�� warto�� w momencie t = 0, a w pozostałym czasie jest równa zeru. Ponadto całka 

1

 Czyli uporz

�dkowanym ci�giem liczb o wspólnej nazwie. 

(2.15)

   99

Elektronika Praktyczna 5/2006

K U R S

Wynik  obliczeń  wskazuje,  że 

moduł  transformaty  jest  równy  jed-

ności,  a różny  od  zera  wykład-

nik  informuje  o przesunięciu  fazo-

wym  sygnału  poddanego  transfor-

macji  względem  sygnału  odniesie-

nia  cos

 

(2πft

 

).

Na  podstawie  pokazanych  przy-

padków,  wykorzystując  odrobinę  de-

dukcji,  dochodzimy  do  wniosku,  że 

jeśli  kształt  sygnału  nie  zmienia 

się,  to  niezależnie  od  jego  przesu-

nięcia  fazowego,  moduł  transforma-

ty  Fouriera  jest  zawsze  jednakowy, 

a zmienia  się  jedynie  jej  faza,  okre-

ślająca  położenie  sygnału  względem 

składowej  kosinusoidalnej.

Jeśli  analizowany  sygnał  będzie 

sumą  kilku  składowych  harmonicz-

nych,  to  moduł  transformaty  Fo-

uriera  będzie  osiągał  lokalnie  mak-

symalne  wartości  dla  częstotliwo-

ści  równych  częstotliwościom  tych 

składowych.  Wynika  to  z faktu,  że 

tylko  dla  tych  składowych  istnieje 

korelacja  między  analizowanym  sy-

gnałem  i odpowiednim  harmonicz-

nym  sygnałem  odniesienia.

Przekształcenie Fouriera 

sygnału dyskretnego

Jak  mogliśmy  się  przekonać, 

transformata  Fouriera  sygnału  cią-

głego  ma  bardzo  klarowną  i intu-

icyjną  interpretację  fizyczną. Obec-

nie  rozpatrzymy  proces  transforma-

cji  Fourierowskiej  sygnału  o czasie 

dyskretnym.  Na  początku  usystema-

tyzujemy  pojęcia  związane  z sygna-

łami  ciągłymi,  dyskretnymi  i cyfro-

wymi  oraz  rzucimy  nieco  światła 

na  sam  proces  próbkowania.

W wyniku  próbkowania  sygnałów 

ciągłych  otrzymujemy  sygnały  o cza-

sie  dyskretnym  nazywane  w litera-

turze  polskiej  sygnałami  dyskretny-

mi

.  Z kolei  sygnał  dyskretny  pod-

dany  kwantyzacji  wartości  chwilo-

wej  i zapisowi  w postaci  ciągu  liczb 

nosi  nazwę  sygnału  cyfrowego.  Sy-

gnał  cyfrowy  jest  więc  sygnałem 

dyskretnym  zarówno  w czasie,  jak 

i −  ze  względu  na  skończoną  ilość 

poziomów  kwantowania  −  w warto-

ści.  Sygnał  cyfrowy,  będący  z pro-

gramowego  punktu  widzenia  wekto-

rem

1

,  może  być  bezpośrednio  pod-

dawany  procedurom  cyfrowego  prze-

twarzania  sygnałów. 

Proces  próbkowania  polega  na 

pomiarze  wartości  sygnału  w ściśle 

określonych  momentach  czasowych. 

W najprostszym  przypadku  mamy 

do  czynienia  z próbkowaniem  rów-

nomiernym  [3, 4],  którego  zasady  są 

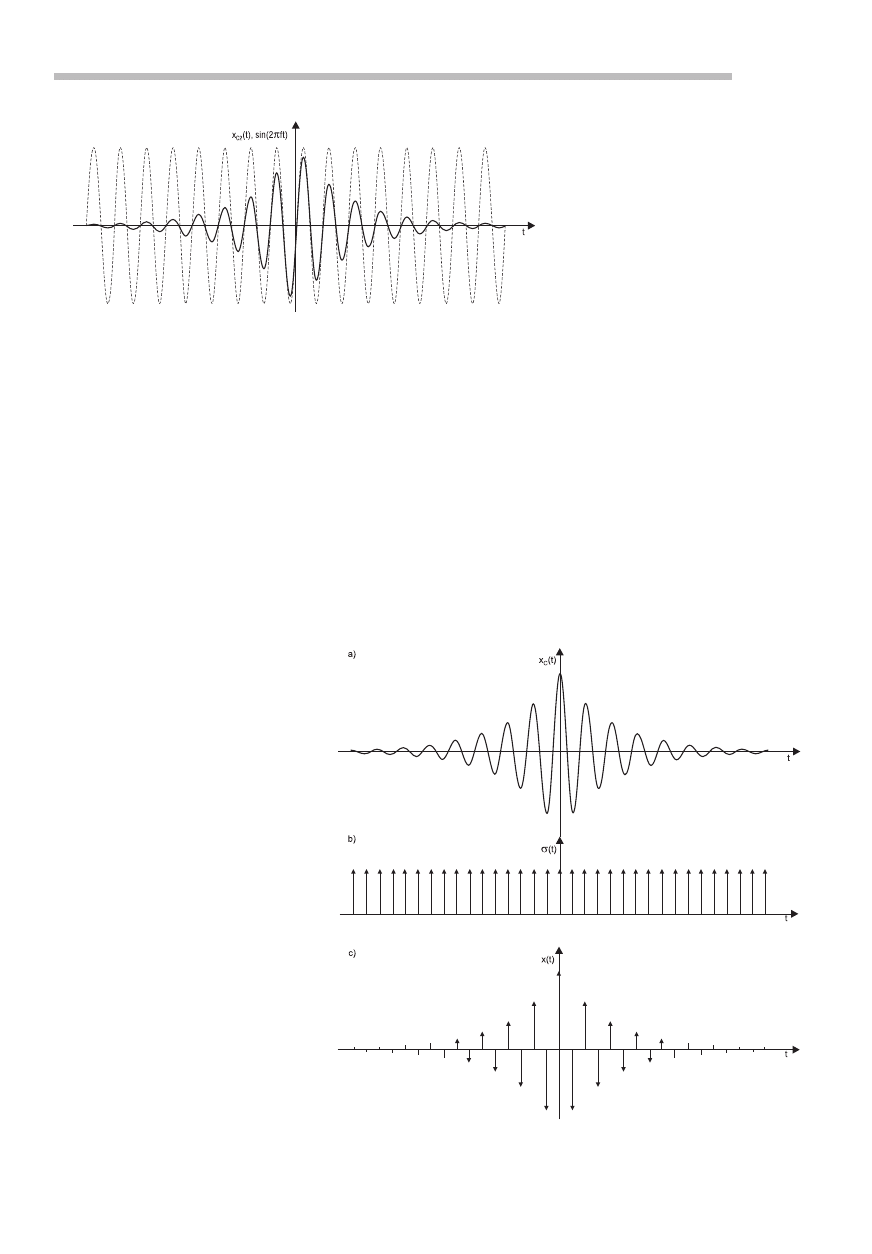
Rys. 15. Proces próbkowania. a) oryginalny sygnał ciągły, b) funkcja próbku-
jąca, c) sygnał dyskretny (na najmniejszych impulsach – ze względu na czy-
telność rysunku – nie zaznaczono grotów strzałek)

określone  przez  twierdzenie  Kotielni-

kowa −

 Shannona.  Proces  próbkowa-

nia  ma  z reguły  miejsce  w większo-

ści  współczesnych  przyrządów  po-

miarowych  oraz  w programach  do 

analizy  układów  elektronicznych. 

W pierwszym  przypadku  próbko-

wanie  jest  realizowane  w celu  póź-

niejszego  zastosowania  wybranych 

algorytmów  CPS  oraz  archiwizacji 

danych  pomiarowych.  W drugim  − 

„próbkowanie”  odbywa  się  „przy-

padkiem”  w wyniku  realizacji  pro-

cedur  całkowania  numerycznego. 

Słowo  próbkowanie  zostało  wzięte 

w cudzysłów,  gdyż  nie  mamy  tu  do 

czynienia  z pomiarem,  lecz  predyk-

cją  wartości  przebiegu  w wybranych 

momentach  czasowych.

W przeciwieństwie  do  przyrzą-

dów  pomiarowych,  programy  re-

alizujące  analizę  czasową  układów 

elektronicznych  z reguły  nie  „prób-

kują”  sygnału  równomiernie,  ale 

praktycznie,  za  pomocą  procedur 

interpolacji  wielomianowej  (najczę-

ściej  liniowej),  dają  w efekcie  koń-

cowym  sygnał  spróbkowany  równo-

miernie  [2].  Z tego  powodu  dalsze 

rozważania  ograniczymy  do  przy-

padku  sygnału  dyskretnego  z jedna-

Rys. 14. Przesunięty o 90°sygnał analizowany (linia ciągła) i sygnał sin

 

(2πft

 

) (li-

nia przerywana) – pełna korelacja

Elektronika Praktyczna 5/2006

100

K U R S

kowym  odstępem  czasowym  między 

sąsiednimi  próbkami. 

Na  samym  początku  rozważań 

w świecie  sygnałów  dyskretnych  po-

jawia  się  pytanie  –  Jak  taki  sy-

gnał  zapisać  analitycznie?  Z pomocą 

przychodzi  nam  teoria  dystrybucji 

z tzw.  deltą  Diraca  δ(t).  Nie  wgłę-

biając  się  w zawiłości  matematycz-

ne,  przyjmijmy  do  wiadomości,  że 

delta  Diraca  ma  nieskończenie  dużą 

wartość  w momencie  t = 0,  a w po-

zostałym  czasie  jest  równa  zeru. 

Ponadto  całka  po  czasie  z impulsu 

Diraca  w granicach  ±∞  jest  równa 

jedności.  Z tego  powodu  delta  Di-

raca  nie  jest  funkcją  w klasycznym 

sensie,  lecz  tzw.  dystrybucją.

Formalnie  dystrybucję  Diraca 

opisuje  się  następująco

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(2.16)

Dystrybucję  δ(t)  przedstawia  się 

graficznie jako wąski prążek za-

kończony  strzałką  o wysokości  rów-

nej  polu  pod  wykresem  dystrybucji, 

a więc  równej  jedności,  umieszczo-

ny  w punkcie  t = 0.

Na  bazie  dystrybucji  δ(t)  moż-

na  utworzyć  tzw.  funkcję  próbkują-

cą  o postaci 

  

 

(2.17)

Funkcja  ta  reprezentuje  ciąg  im-

pulsów  Diraca  o jednostkowej  wy-

sokości,  ułożonych  na  osi  czasu 

w jednakowych  odstępach,  równych 

okresowi  próbkowania  T

S 

(sampling).

Spróbkowana  wersja  x

 

(

 

t

 

)  sygna-

łu  ciągłego  x

C 

(

 

t

 

)  może  być  przed-

stawiona  jako  iloczyn  sygnału  x

C 

(

 

t

 

) 

i funkcji  próbkującej

Cały  proces  próbkowania,  prze-

prowadzony  zgodnie  z twierdzeniem 

Kotielnikowa − Shannona,  jest  zilu-

strowany  na 

rys.  15.

Ponieważ  funkcja  próbkująca, 

a tym  samym  sygnał  x

 

(

 

t

 

),  są  określo-

ne  w dyskretnych  momentach  czasu

często  stosuje  się  zapis  wyraźnie 

wskazujący,  że  mamy  do  czynienia 

z wektorem

 

 

  

 

Stosując  klasyczną  transforma-

tę  Fouriera  do  sygnału  dyskretnego 

x

 

(

 

n

 

),  możemy  napisać

 

 

  

 

  

 

 

(2.20)

Zmieniając  kolejność  całkowania 

i sumowania,  otrzymujemy

 

   

   

(2.21)

Ponieważ

 

 

  

 

  

(2.22)

ostatecznie  otrzymujemy

 

  

(2.23)

W punktach  t = nT

S

  zachodzi 

równość

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

(2.18)

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

(2.19)

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

3

po czasie z impulsu Diraca w granicach 

±∞ jest równa jedno�ci. Z tego powodu delta Diraca nie jest 

funkcj

� w klasycznym sensie, lecz tzw. dystrybucj�.

Formalnie dystrybucj

� Diraca opisuje si� nast�puj�co

( )

( )

�

�

�

�

��

�

�

�

�

�

�

=

δ

�

�

�

≠

=

∞

=

δ

∞

∞

-

1

d

0

dla

0

0

dla

t

t

t

t

t

 

(2.16) 

Dystrybucj

� δ(t) przedstawia si� graficznie jako w�ski pr��ek zako�czony strzałk� o wysoko�ci

równej polu pod wykresem dystrybucji, a wi

�c równej jedno�ci, umieszczony w punkcie t = 0. 

Na bazie dystrybucji 

δ(t) mo�na utworzy� tzw. funkcj� próbkuj�c� o postaci  

( )

(

)

�

∞

∞

=

−

δ

=

σ

-

n

S

nT

t

t

 

(2.17) 

Funkcja ta reprezentuje ci

�g impulsów Diraca o jednostkowej wysoko�ci, uło�onych na osi czasu w 

jednakowych odst

�pach, równych okresowi próbkowania T

S

(sampling).

Spróbkowana wersja x ( t ) sygnału ci

�głego x

C

( t ) mo

�e by� przedstawiona jako iloczyn sygnału 

x

C

( t ) i funkcji próbkuj

�cej 

( )

( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

σ

=

-

n

S

C

C

nT

t

t

x

t

t

x

t

x

 

(2.18) 

Cały proces próbkowania, przeprowadzony zgodnie z twierdzeniem Kotielnikowa 

− Shannona, jest 

zilustrowany na rys. 15.

Rys. 15. Proces próbkowania. a) oryginalny sygnał ci

�gły, b) funkcja próbkuj�ca, c) sygnał dyskretny 

(na najmniejszych impulsach – ze wzgl

�du na czytelno�� rysunku – nie zaznaczono grotów strzałek) 

Poniewa

� funkcja próbkuj�ca, a tym samym sygnał x ( t ), s� okre�lone w dyskretnych momentach 

czasu

...

,

2

,

1

,

0

,

±

±

=

=

n

nT

t

S

cz

�sto stosuje si� zapis wyra�nie wskazuj�cy, �e mamy do czynienia z wektorem 

( ) ( ) ( )

( ) (

)

�

∞

∞

=

−

δ

=

=

=

-

n

S

S

C

S

nT

t

nT

x

n

x

nT

x

t

x

 

(2.19) 

 

Stosuj

�c klasyczn� transformat� Fouriera do sygnału dyskretnego x ( n ), mo�emy napisa�

( )

( ) (

)

( )

(

)

�

�

�

−

δ

=

�

�

�

−

δ

=

∞

∞

−

∞

−∞

=

π

−

∞

∞

−

π

−

∞

−∞

=

�

�

t

nT

t

nT

x

t

nT

t

nT

x

f

X

n

S

nT

f

S

C

nT

f

n

S

S

C

S

S

d

e

d

e

2

j

2

j

 

(2.20) 

Zmieniaj

�c kolejno�� całkowania i sumowania, otrzymujemy 

( )

( )

(

)

( )

(

)

�

�

∞

−∞

=

∞

−∞

=

∞

∞

−

π

−

π

−

∞

∞

−

�

�

�

−

δ

=

−

δ

�

�

�

=

n

n

S

nT

f

S

C

S

nT

f

S

C

t

nT

t

nT

x

t

nT

t

nT

x

f

X

S

S

d

e

d

e

2

j

2

j

 

(2.21) 

Poniewa

�

(

)

1

d

=

�

�

�

−

δ

∞

∞

−

t

nT

t

S

 

(2.22) 

ostatecznie otrzymujemy 

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

C

S

nT

x

f

X

2

j

e

 

(2.23) 

W punktach t = nT

S

 zachodzi równo

��

 

 

 

 

więc

 

  

(2.25)

Ponieważ  w wykładniku  w miej-

scu  t  pojawił  się  iloczyn  nT

S

,  mo-

żemy  stwierdzić,  że  widmo  sygna-

łu  spróbkowanego  jest  okresowe, 

a okres  jest  równy  T

S

.  Maksymalna 

częstotliwość,  dla  której  sensowne 

jest  badanie  widma

2

,  jest  więc  rów-

na  częstotliwości  próbkowania  (sam-

pling  frequency

)  określonej  wzorem

   

 

 

 

  

 

 

(2.26)

Skoro  dotarliśmy  aż  tutaj,  śmia-

ło  możemy  przystąpić  do  lektu-

ry  ostatniej  części  cyklu  omawia-

jącej  dyskretne  przekształcenia  Fo-

uriera  (DFT)  i przykład  jego  realiza-

cji  praktycznej.

Andrzej  Dobrowolski

http://adobrowolski.wel.wat.edu.pl

Literatura

1. Cooley  J.,  Tuckey  J.,  „An  algo-

rithm  for  the  machine  compu-

tation  of  complex  Fourier  se-

ries

”,  Math.  Comput.,  vol.  19 

(90),  1965

2. Dobrowolski  A.,  „Pod  maską 

SPICE’a.  Metody  i algorytmy 

analizy  układów  elektronicz-

nych

”,  BTC,  Warszawa,  2004

3. Lyons  R.  G.,  „Wprowadze-

nie  do  cyfrowego  przetwarza-

nia  sygnałów

”,  WKŁ,  Warsza-

wa,  1999

4. Oppenheim  A.  V.,  Schafer  R. 

W.,  „Cyfrowe  przetwarzanie 

sygnałów

”,  WKŁ,  Warszawa, 

1979

5. Szabatin  J.,  „Podstawy  teorii 

sygnałów

”,  WKŁ,  Warszawa, 

2000

1

  Czyli  uporządkowanym  ciągiem 

liczb  o wspólnej  nazwie.

2

  W przypadku  sygnału  okresowe-

go  jego  widmo  powtarza  się  po-

wyżej  częstotliwości  będącej  od-

 

4

( ) ( )

S

S

C

nT

x

nT

x

=

 

(2.24) 

wi

�c

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

S

nT

x

f

X

2

j

e

 

(2.25) 

Poniewa

� w wykładniku w miejscu t pojawił si� iloczyn nT

S

, mo

�emy stwierdzi�, �e widmo sygna-

łu spróbowanego jest okresowe, a okres jest równy T

S

. Maksymalna cz

�stotliwo��, dla której sen-

sowne jest badanie widma

1

, jest wi

�c równa cz�stotliwo�ci próbkowania (sampling frequency)

okre

�lonej wzorem 

S

S

T

f

1

=

 

(2.26) 

Skoro dotarli

�my a� tutaj, �miało mo�emy przyst�pi� do lektury ostatniej cz��ci cyklu omawiaj�cej

dyskretne przekształcenia Fouriera (DFT) i przykład jego realizacji praktycznej. 
Andrzej Dobrowolski 
+ STRONA JAK MIESIAC TEMU

Literatura 
1. Cooley J., Tuckey J., „An algorithm for the machine computation of complex Fourier series”,
Math. Comput., vol. 19 (90), 1965 
2. Dobrowolski A., „Pod mask

� SPICE’a. Metody i algorytmy analizy układów elektronicznych”, 

BTC, Warszawa, 2004 
3. Lyons R. G., „Wprowadzenie do cyfrowego przetwarzania sygnałów”, WKŁ, Warszawa, 1999 
4. Oppenheim A. V., Schafer R. W., „Cyfrowe przetwarzanie sygnałów”, WKŁ, Warszawa, 1979 
5. 

Szabatin J., „Podstawy teorii sygnałów”, WKŁ, Warszawa, 2000 

1

 W przypadku sygnału okresowego jego widmo powtarza si

� powy�ej cz�stotliwo�ci b�d�cej odwrotno�ci� okresu. 

 

4

( ) ( )

S

S

C

nT

x

nT

x

=

 

(2.24) 

wi

�c

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

S

nT

x

f

X

2

j

e

 

(2.25) 

Poniewa

� w wykładniku w miejscu t pojawił si� iloczyn nT

S

, mo

�emy stwierdzi�, �e widmo sygna-

łu spróbowanego jest okresowe, a okres jest równy T

S

. Maksymalna cz

�stotliwo��, dla której sen-

sowne jest badanie widma

1

, jest wi

�c równa cz�stotliwo�ci próbkowania (sampling frequency)

okre

�lonej wzorem 

S

S

T

f

1

=

 

(2.26) 

Skoro dotarli

�my a� tutaj, �miało mo�emy przyst�pi� do lektury ostatniej cz��ci cyklu omawiaj�cej

dyskretne przekształcenia Fouriera (DFT) i przykład jego realizacji praktycznej. 
Andrzej Dobrowolski 
+ STRONA JAK MIESIAC TEMU

Literatura 
1. Cooley J., Tuckey J., „An algorithm for the machine computation of complex Fourier series”,
Math. Comput., vol. 19 (90), 1965 
2. Dobrowolski A., „Pod mask

� SPICE’a. Metody i algorytmy analizy układów elektronicznych”, 

BTC, Warszawa, 2004 
3. Lyons R. G., „Wprowadzenie do cyfrowego przetwarzania sygnałów”, WKŁ, Warszawa, 1999 
4. Oppenheim A. V., Schafer R. W., „Cyfrowe przetwarzanie sygnałów”, WKŁ, Warszawa, 1979 
5. 

Szabatin J., „Podstawy teorii sygnałów”, WKŁ, Warszawa, 2000 

1

 W przypadku sygnału okresowego jego widmo powtarza si

� powy�ej cz�stotliwo�ci b�d�cej odwrotno�ci� okresu. 

(2.24)

 

4

( ) ( )

S

S

C

nT

x

nT

x

=

 

(2.24) 

wi

�c

( )

( )

�

∞

−∞

=

π

−

=

n

nT

f

S

S

nT

x

f

X

2

j

e

 

(2.25) 

Poniewa

� w wykładniku w miejscu t pojawił si� iloczyn nT

S

, mo

�emy stwierdzi�, �e widmo sygna-

łu spróbowanego jest okresowe, a okres jest równy T

S

. Maksymalna cz

�stotliwo��, dla której sen-

sowne jest badanie widma

1

, jest wi

�c równa cz�stotliwo�ci próbkowania (sampling frequency)

okre

�lonej wzorem 

S

S

T

f

1

=

 

(2.26) 

Skoro dotarli

�my a� tutaj, �miało mo�emy przyst�pi� do lektury ostatniej cz��ci cyklu omawiaj�cej

dyskretne przekształcenia Fouriera (DFT) i przykład jego realizacji praktycznej. 
Andrzej Dobrowolski 
+ STRONA JAK MIESIAC TEMU

Literatura 
1. Cooley J., Tuckey J., „An algorithm for the machine computation of complex Fourier series”,
Math. Comput., vol. 19 (90), 1965 
2. Dobrowolski A., „Pod mask

� SPICE’a. Metody i algorytmy analizy układów elektronicznych”, 

BTC, Warszawa, 2004 
3. Lyons R. G., „Wprowadzenie do cyfrowego przetwarzania sygnałów”, WKŁ, Warszawa, 1999 
4. Oppenheim A. V., Schafer R. W., „Cyfrowe przetwarzanie sygnałów”, WKŁ, Warszawa, 1979 
5. 

Szabatin J., „Podstawy teorii sygnałów”, WKŁ, Warszawa, 2000 

1

 W przypadku sygnału okresowego jego widmo powtarza si

� powy�ej cz�stotliwo�ci b�d�cej odwrotno�ci� okresu. 

forum.ep.com.pl