Obliczanie niepewności pomiarowych.
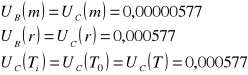
Dla osi OX
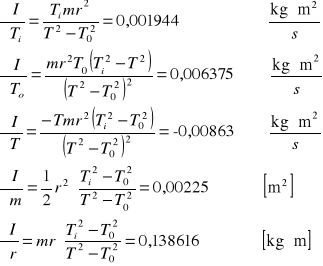
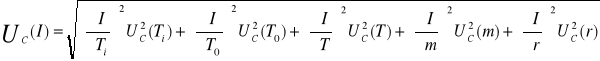
![]()
dla![]()
=0,95 k=2
![]()
Dla osi OY
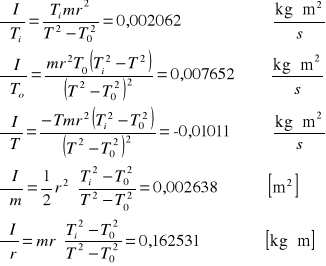
![]()
dla![]()
=0,95 k=2
![]()
Dla osi OZ
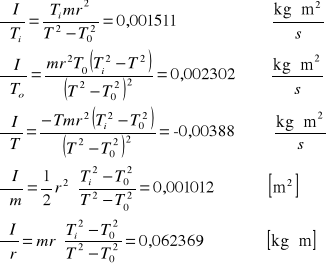
![]()
dla![]()
=0,95 k=2
![]()
Wnioski:
Zaobserwowaliśmy, że obliczone momenty bezwładności badanej bryły względem poszczególnych osi obrotu różnią się.
Niedoskonałości pomiarów w głównej mierze pochodziły od źle napiętego drutu i chybotliwego stołu.
Podstawy teoretyczne.
Momentem bezwładności nazywamy sumę iloczynów mas wszystkich punktów materialnych ciała i kwadratu odległości od osi obrotu:
![]()
Moment bezwładności tego układu nie jest równy momentowi bezwładności ciała sztywnego, lecz będzie do niego dążył, gdy liczba sześcianików dążyć będzie do nieskończoności. Zatem momentem bezwładności ciała sztywnego jest granicą momentu bezwładności I:
![]()
Wyprowadzenie wzoru na moment bezwładności walca:
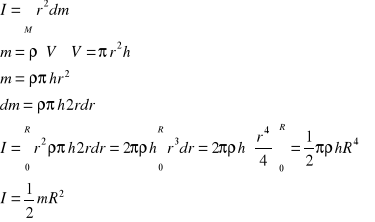
Wyprowadzenie wzoru roboczego
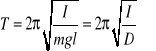
- D - moment kierujący wahadła
![]()
- okres drgań przy nieobciążonym stoliku
![]()
- okres drgań przy obciążeniu bryłą foremną o znanym momencie bezwładności
Podnosząc powyższe równania do kwadratu, a następnie odejmując stronami otrzymamy:
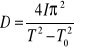
![]()
- okres drgań przy obciążeniu bryłą o nieznanym momencie bezwładności
Podnosząc równania na ![]()
do kwadratu, a następnie odejmując stronami otrzymamy:
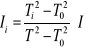
Wyszukiwarka
Podobne podstrony:
wahadło Oberbecka, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
laborka na za tydzień, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
WYZNACZANIE CIEP A MOLOWEGO, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
01, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
PR FALI, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
NAPI C 1, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
Ćw 12 a, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
Wyznaczanie równoważnika elektrochemicznego miedzi, laboratorium fizyczne, Laboratorium semestr 2 RÓ
37 - wersja 1, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
CPCV, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
Ćw. 1, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
teoria do 6, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
ćw 5, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
fiz. 1, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
ćw. 06 lab-fiz, laboratorium fizyczne, Laboratorium semestr 2 RÓŻNE
więcej podobnych podstron