Tomasz Pajączkowski

25.04.2001

Ćwiczenie nr 1.

Temat: Wyznaczanie gęstości ciała stałego za pomocą piknometru.

Tabela wyznaczonych wartości:

masa [g]	I ) ołów	II ) kamyki
m1	62,7	62,7
m2	106,1	81,2
m3	130,6	103,15
m4	91,2	91,15

Teoria zjawiska:

Gęstość jest jedną z podstawowych wielkości fizycznych charakteryzujących różne substancje. Gęstością nazywamy stosunek masy danego ciała do jego objętości

Jak wynika z powyższej zależności gęstość jest odwrotnie proporcjonalna do objętości ρ ~ V^-1. Ponieważ objętość zależy od zmiany temperatury i ciśnienia, w sposób pokazany poniżej, gęstość zależy również od tych czynników.

V(T) = V₀ ( 1 - αΔT )

V(p) = V0 ( 1 - βΔT ) gdzie α,β - współczynniki proporcjonalności

Gęstość substancji z reguły zwiększa się ze wzrostem ciśnienia i maleje ze wzrostem temperatury. Przy przejściu substancji ze stanu ciekłego w gazowy oraz ze stanu stałego w ciekły ( przy parowaniu i topnieniu ) gęstość maleje skokowo. Wyjątkiem jest gęstość lodu i żelaza, która po ich stopieniu zwiększa się.

Jednostką gęstości w układzie SI jest kg/m³, jednak jednostką tradycyjnie stosowaną jest g/cm³.

Wyprowadzenie wzoru roboczego:

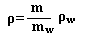
Gęstość ciała określa się jako stosunek masy do zajmowanej objętości ρ=m/V. Stosując powyższy wzór do wyznaczenia gęstości wody destylowanej otrzymujemy: ρ_w=m_w/V, stąd V=m_w/ρ_w. Po podstawieniu wartość gęstości badanego ciała stałego można określić wzorem:

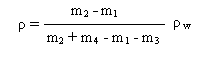
Masa m ciała stałego równa jest różnicy masy piknometru wypełnionego ciałem i masy pustego piknometru: m = m₁ - m₂. Masa wody natomiast jest masą wypartą przez ciało stałe: m_w = m₂ + m₄ - m₁ - m₃, gdzie m₃ jest masą piknometru z ciałem stałym i wodą, zaś m₄ jest masą piknometru z wodą. Można zatem zapisać wzór końcowy:

Opis ćwiczenia z opisem przeprowadzonego eksperymentu:

Celem ćwiczenia było wyznaczenie gęstości ciała stałego, a dokładniej ołowiu i kamieni przy wykorzystaniu piknometru. Pomiar gęstości w tej metodzie sprowadza się do wyznaczenia wartości masy pustego piknometru - m₂, masy piknometru wypełnionego ciałem stałym do ok. 1/3 jego objętości - m₁, jest masą piknometru z ciałem stałym i wodą - m₃ oraz masą piknometru z wodą - m₄ i następnie podstawieniu ich do powyższego wzoru.

Piknometrem nazywamy kolbę szklaną, zamkniętą dokładnie doszlifowanym korkiem, w którym znajduje się kapilarny otwór.

Przed przystąpieniem do wykonywanego oznaczenia piknometr należy starannie umyć a następnie dokładnie osuszyć. Po wykonaniu powyższego należy wyznaczyć masę pustego piknometru, co też uczyniłem. Następnie piknometr napełniłem kulkami ołowiu do objętości 1/3 poczym wyznaczyłem masę m₂. Następnie piknometr uzupełniłem wodą destylowaną i wyznaczyłem masę m₃. Opróżniłem piknometr, starannie go przemywając, poczym całą jego objętość wypełniłem wodą destylowaną poczym wyznaczyłem masę m₄. Pomiaru masy dokonywałem na wadze analitycznej.

Powyższe czynności powtórzyłem dla kamieni. Wartości wyznaczone w czasie pomiaru umieściłem w powyższej tabeli a następnie na ich podstawie dokonałem końcowych obliczeń i wyciągnąłem ostateczne wnioski.

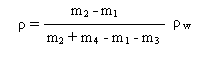
Obliczenia do wykonanego ćwiczenia:

Po podstawieniu wyznaczonych wartości do powyższego wzoru otrzymana wartość ρ wynosiła: I ) dla ołowiu ρ = 10,85g\cm³ II ) dla kamyków ρ = 2,85g\cm³.

Szacowanie niepewności pomiaru:

Wprowadzę podstawienie: M₁= m₂ - m₁ oraz M₂ = m₂ + m₄ - m₁ - m₃. Wówczas nasz wzór ma postać: ρ =( M₁/ M ₂ )·ρ_w.

Niepewność całkowita dla M₁:

Δx(m₁) = Δx(m₂) = 0,01·10^-3kg

U_B(m₁) = U_B(m₂) = Δx(m)/3^1/2 = 0,058·10^-3kg

U_C( M₁) = [ U_B²(m₁) + U_B²(m₂) ]^1/2 = 0,0082·10^-3kg

Niepewność całkowita dla M₂:

Δx(m₁) = Δx(m₂) = Δx(m₃) = Δx(m₄) = 0,01·10^-3kg

U_B(m₁) = U_B(m₂) = U_B(m₃) = U_B(m₄) = Δx(m)/3^1/2 = 0,058·10^-3kg

U_C( M₁) = [ U_B²(m₁) + U_B²(m₂) + U_B²(m₃) + U_B²(m₄) ]^1/2 = 0,0082·10^-3kg

Niepewność całkowita dla ρ_w:

Δx(ρ_w) = 0,1kg/m³

U_C(ρ_w) = Δx(ρ_w)/3^1/2 = 0,058kg/m³

Wartości pochodnych cząstkowych dla ołowiu:

ðρ/ðρ_w = M₁/M₂ = 10,85

ðρ/ðM₁ = ρ_w/M₂ = 0,25·10^-3kg/m³

ðρ/ðM₂ = -ρ_wM₁/M₂² = 2,70·10^-3kg/m³

U_C = 0,63kg/m³

U = k·U_C = 1,26kg/m³ dla α = 0,95

Wartości pochodnych cząstkowych dla kamieni:

ðρ/ðρ_w = M₁/M₂ = 2,85

ðρ/ðM₁ = ρ_w/M₂ = 0,15·10^-3kg/m³

ðρ/ðM2 = -ρwM1/M2² = 0,44·10-3kg/m³

UC(ρ) = 0,17kg/m³

U = k·U_C = 0,34kg/m³ dla α = 0,95

Ostatecznie wyznaczona wartość gęstości wynosi:

ρ = ( 10,85 ± 1,26 )·10³ kg/m³ dla ołowiu

ρ = ( 2,85 ± 0,34 )·10³ kg/m³ dla kamieni

Wnioski:

Wyznaczone wartości gęstości wynoszą: ρ = ( 10,85 ± 1,26 )·10³ kg/m³ dla ołowiu i ρ = ( 2,85 ± 0,34 )·10³ kg/m³ dla kamieni. Wartości te wyznaczone są dla temperatury 24°C.

Wartość wyznaczona dla ołowiu nieznacznie różni się od wartości odczytanej z Tablic Chemicznych (Wydanie II, zmienione i rozszerzone Warszawa 1997) dla temperatury 25°C wynosi 11,34·10³ kg/m³, co zaprzecza fakt opisany powyżej, jednoznacznie wskazując na błąd oznaczenia. Spowodowane to mogło być małą dokładnością metody jak również tym, że przy wykonywaniu ćwiczenia dokonaliśmy wyznaczenia ρ kulek śrutu a nie czystego ołowiu.

Porównanie wyznaczonej wartości gęstości dla kamieni z wartością z tablic było niemożliwe gdyż nie byliśmy w stanie zidentyfikować minerału jaki stanowiły. Możliwe jest jedynie szacunkowe porównanie otrzymanej wartości, która w tym przypadku winna zawierać się w granicach 2,3 - 2,9 w przypadku skał pochodzenia wulkanicznego. Dowodzi to poprawności wykonanego oznaczenia.

Stałe:

T = 24°C

ρ_w = 0,9972g/cm³

---