Podobieństwo trójkątów
Cechy podobieństwa trójkątów, to warunki konieczne i wystarczające na to, aby dwa trójkąty były podobne.
I cecha podobieństwa trójkątów |
(bbb) Jeśli trzy boki jednego trójkąta są proporcjonalne do trzech boków drugiego trójkąta, to te dwa trójkąty są podobne.
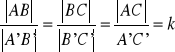
k - skala podobieństwa
ABC ~ A'B'C'
Zapis: ABC ~ A'B'C' czytamy: trójkąt ABC jest podobny do trójkąta A'B'C'
II cecha podobieństwa trójkątów |
(kkk) Jeśli dwa kąty jednego trójkąta są odpowiednio równe kątom drugiego trójkąta, to te dwa trójkąty są podobne.
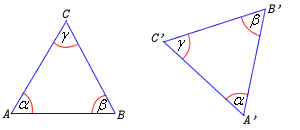
III cecha podobieństwa trójkątów |
(bkb) Jeśli dwa boki jednego trójkąta są proporcjonalne do dwóch boków drugiego trójkąta i kąty zawarte między tymi bokami są równe, to te dwa trójkąty są podobne.
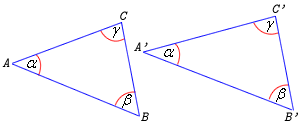
Aby stwierdzić, czy dwa trójkąty są podobne, wystarczy skorzystać z jednej z cech podobieństwa trójkątów (w zależności od danych w zadaniu) .
Przykład
Czy narysowane trójkąty są podobne, jeżeli
A
K
C B M L
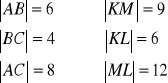
?
Rozwiązanie
Ponieważ dane mamy długości wszystkich boków w obu trójkątów , to korzystamy z cechy bbb i sprawdzamy, czy boki jednego trójkąta są odpowiednio proporcjonalne do boków drugiego trójkąta.
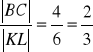
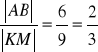
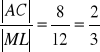
Zatem ABC ~ L.
Ćwiczenie 1
Rozwiąż zadania:1,2,3 str. 218-219 z podręcznika.
Z cechami podobieństwa trójkątów związane są twierdzenie Talesa i twierdzenie odwrotne do twierdzenia Talesa.
Twierdzenie Talesa
Jeżeli ramiona kąta przecięte są prostymi równoległymi, to stosunki długości odcinków wyznaczonych przez te proste na jednym ramieniu kąta, są równe stosunkom długości odpowiednich odcinków na drugim ramieniu kąta.
Na przykład:
|OA|:|OB| = |OA′|:|OB′|
|OA|:|AB| = |OA′|:|A′B′| itd.
lecz również, o czym często się zapomina:
|OC|:|AC| = |OC′|:|A′C′| itd.
Wniosek
W sytuacji jak na rysunku, z twierdzenia Talesa wynika następująca proporcja:
|OA |:|OB | = |AA′ |:|BB′ |
często również nazywana (mylnie) twierdzeniem Talesa.
Twierdzenie odwrotne
Przestawiając założenia twierdzenia z tezą, otrzymujemy twierdzenie odwrotne do danego. Twierdzenie odwrotne często nie jest prawdziwe, dlatego przypadki, w których jednak ono zachodzi, są szczególnie godne uwagi. Tak jest właśnie z twierdzeniem Talesa.
Twierdzenie odwrotne do twierdzenia Talesa
Jeżeli ramiona kąta przecięte są kilkoma prostymi i stosunki długości odcinków na jednym ramieniu kąta równe są stosunkom długości odpowiednich odcinków na drugim ramieniu kąta, to dane proste są równoległe.
Zastosowania
Twierdzenie Talesa ma liczne zastosowania praktyczne i teoretyczne. Oto kilka z nich.
Pomiar wysokości drzewa
Wystarczy drążek o znanej długości, taśma miernicza i odrobina sprytu, by poznać wysokość każdego drzewa. Drążek należy ustawić w takiej odległości od drzewa, by celując z ziemi, jego wierzchołek zrównał się z wierzchołkiem drzewa. Mierzymy wówczas odległości: od podstawy pnia do miejsca, z którego celowaliśmy oraz do drążka - i dokonujemy obliczeń według podanego wyżej wzoru
Pomiar wysokości piramidy
Według legendy Tales wyznaczył wysokość piramidy w Egipcie na podstawie długości cienia rzucanego przez kij, czym wprawił w zdumienie kapłanów. Oto jak tego dokonał.
Na podstawie wniosku z twierdzenia Talesa zachodzi proporcja |OA|:|OB| = |AA′|:|BB′| skąd |BB′|=|AA′|·|OB|:|OA|. Znając |AA′| - długość kija, mierząc |OA| - długość jego cienia i |OB| - długość cienia piramidy, natychmiast wyliczamy jej wysokość
Analogicznie można obliczać wysokość innego wysokiego przedmiotu.
Pomiar odległości statku od brzegu
Z wniosku z twierdzenia Talesa mamy:
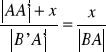
skąd (po przekształceniu)
x = 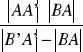
|.
Mierząc długości odcinków występujących w tej równości wyznaczamy x.
Podział odcinka w danym stosunku
Dane są dwa odcinki o długościach a i b. Dany odcinek AB podzielić w stosunku a:b.
Rzut oka na rysunek i twierdzenie Talesa pozwalają stwierdzić, że punkt P dzieli odcinek w wymaganym stosunku. Powyższa konstrukcja była podstawą greckiej arytmetyki - pozwalała mnożyć i dzielić odcinki, które Grecy utożsamiali z liczbami.
Ćwiczenie 2
Rozwiąż zadania: 9, 11,13,15 str. 220-221 z podręcznika.
.
Wyszukiwarka
Podobne podstrony:
Policz ile jest trójkątów, matematyka w kształceniu zintegrowanym
figury trójkąt, Matematyka
okrąg wpisany w trójkąt, Matematyka, Gimnazjum
Cechy podobieństwa trójkątów
Podobieństwo trójkątów
trójkąt 30;60;90 i 45;45;90, Matematyka, Gimnazjum
trojkaty(1), Przedszkole, Karty pracy-przedszkole, edukacja matematyczna
matematyka, Przystawanie figur, Podobieństwo figur
Trójkąt, dla dzieci, ćwiczenia matematyczne
5.TROJKATY-klasyfikacja-ukladanka.b, Matematyka, KLASA 5 - matematyka
E akademia Matematyka Podobieństwo figur
Jeżeli trójkąt jest prostokątny, Matemayka
trójkąty - podstawówka, matematyka podstawówka
TRÓJKĄTY JAKO FIGURY GEOMETRYCZNE PŁASKIE I ICH NAJWAŻNIEJSZE ELEMENTY, Matematyka
5.TROJKATY-domino, Matematyka, KLASA 5 - matematyka
Pod górę i z góry. Intuicje geometryczne - trójkąt., scenariusze zajęć - matematyka
więcej podobnych podstron