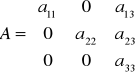
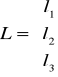
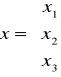
Oznaczenia:

Układ równań poprawek:

A^TA x + A^TL = 0,

A^TA x = -A^TL - oznaczam jako Ux = b

Następnie po dokonaniu redukcji niewiadomych (części niewiadomych układu) -

przyjmuję następujące oznaczenia:

Rx = b_R

Układ równań dla 3 grup niewiadomych

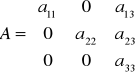
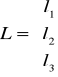
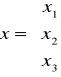
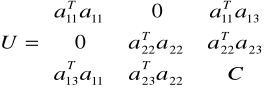
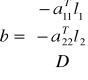
Po redukcji niewiadomych z grup I i II otrzymujemy

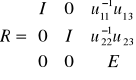
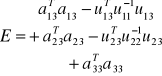
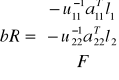
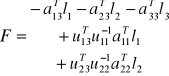
Rozpatrzenie układu równań dla niewiadomych z grup I i III

- macierz obejmująca tylko obserwacje z 1 wiersza macierzy A

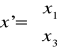
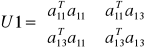
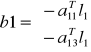
Po redukcji niewiadomych z I grupy

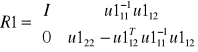
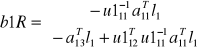
Rozpatrzenie układu równań dla niewiadomych z grup II i III

- macierz obejmująca tylko obserwacje z 2 wiersza macierzy A

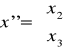
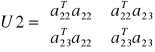
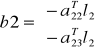
Po redukcji niewiadomych z I grupy

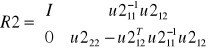
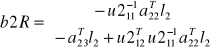
Porównanie z układem równań dla wszystkich trzech grup

Porównując układy równań rozwiązane dla grup (I, III) oraz (II, III) z pełnym układem równań można zauważyć, że 3 zespół wierszy zredukowanej macierzy U (czyli macierzy R) oraz odpowiedni wektor wyrazów wolnych można wyrazić za pomocą macierzy i wektorów uzyskanych w redukcji dla poszczególnych grup, czyli

,

Dzięki tym zależnościom po wykonaniu redukcji dla grup (I, III) oraz (II, III) można łatwo obliczyć niewiadome z grupy III (uwzględniając naturalnie tylko 3 zespół wierszy macierzy R).

Po wyliczeniu niewiadomych z grupy łącznej, na podstawie macierzy R1 i R2 uzyskujemy niewiadome z pozostałych grup.

---