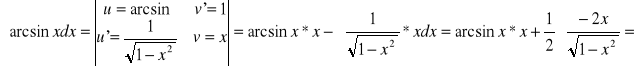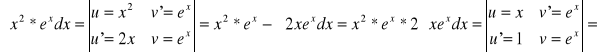Całkowani przez podstawianie
Tw. Jeżeli f(x) jest ciągła w (a,b) i … jest ciągła w … i istnieje ciągła … to zachodzi wzór
![]()
Należy przy tym pamiętać, że podstawienie ma całkę upraszczać
Np.
1. Metoda tożsamościowego przekształcenia
a) ![]()
![]()
2. Metoda przez podstawienie:
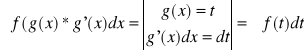
a) 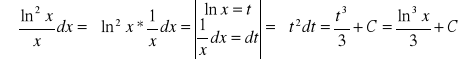
b) 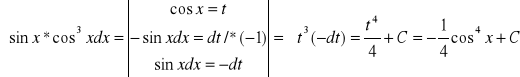
c) 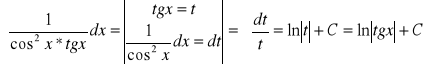
d) 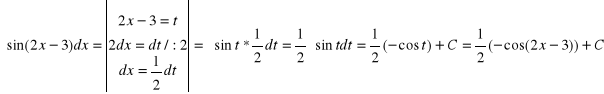
w tym przykładzie można obliczyć całkę bez podstawiania korzystając ze wzoru:
![]()
Jeżeli ![]()
Wówczas ![]()
3. Jeżeli mamy ![]()
to można korzystać ze wzoru:
![]()
nie wykorzystując za każdym razem podstawienia za f(x) np.
![]()
4. ![]()
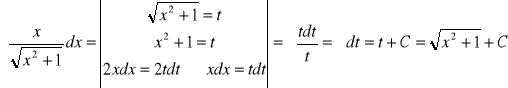
Do wyniku tego dojdziemy też ze wzoru
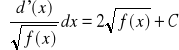
Mamy ![]()
Całkowanie przez części
Tw. Jeżeli funkcje ![]()
i ![]()
mają ciągłe pochodne w X to zachodzi wzór
![]()
Dowód: Obliczamy pochodne obydwu stron
L: ![]()
P: ![]()
Stąd wynika L=P
Przykład
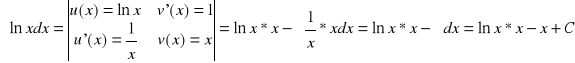
Czasami obliczenie całki będzie łączyć te dwie metody jednocześnie:
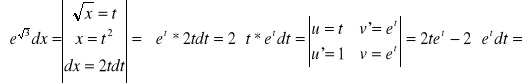
![]()
Są przykłady gdzie stosowanie metody całkowania przez części przerywamy w momencie gdy wrócimy do całki wyjściowej np.:
![]()
; ![]()
; ![]()
; ![]()
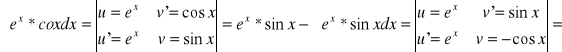
![]()
![]()
![]()
mgr Barbara Pakleza Matematyka 23.02.08
Wykład 1
- 1 -
Wyszukiwarka
Podobne podstrony:
Matematyka - Wykład 4, Studia, ZiIP, SEMESTR II, Matematyka
Matematyka - Wykład 5, Studia, ZiIP, SEMESTR II, Matematyka
Matematyka - Wykład 3, Studia, ZiIP, SEMESTR II, Matematyka
Makroekonomia - Wykład 5, Studia, ZiIP, SEMESTR II, Makroekonomia
Makroekonomia - Wykład 6, Studia, ZiIP, SEMESTR II, Makroekonomia
Makroekonomia - Wykład 7, Studia, ZiIP, SEMESTR II, Makroekonomia
Makroekonomia - Wykład 2, Studia, ZiIP, SEMESTR II, Makroekonomia
Makroekonomia - Wykład 3, Studia, ZiIP, SEMESTR II, Makroekonomia
Makroekonomia - Wykład 4, Studia, ZiIP, SEMESTR II, Makroekonomia
Mat met Wykład 1, Studia, ZiIP, SEMESTR II, Materiały metalowe
Matematyka sem III wyklad 2, Studia, ZiIP, SEMESTR III, Matematyka
Filozofia wykład 2, Studia, ZiIP, SEMESTR V, Fizozofia
Stale Konstrukcujne, Studia, ZiIP, SEMESTR II, Materiały metalowe
materiały metalowe zestaw 4, Studia, ZiIP, SEMESTR II, Materiały metalowe, kartkówka 1
Obróbka cieplna mini, Studia, ZiIP, SEMESTR II, Materiały metalowe
Mechanika lab ćw C, Studia, ZiIP, SEMESTR II, Mechanika
ZESTAWY PYTAŃ Z PNOM, Studia, ZiIP, SEMESTR II, Materiały metalowe, kartkówka 1
Filozofia wykład 1, Studia, ZiIP, SEMESTR V, Fizozofia
więcej podobnych podstron