Temat: Wyznaczanie modułu sztywności metodą dynamiczną
Numer pary: 7
Numer ćwiczenia: 10
I. Opis teoretyczny
1. Prawo Hooke'a
Prawo Hooke'a formułuje zależność między naprężeniem a odkształceniem :
Naprężenie wewnętrzne (będące skutkiem odkształcenia) jest wprost proporcjonalne do odkształcenia. W omawianym przykładzie ma ono prosty zapis:
τ = G γ
Gdzie:
τ - naprężenie styczne (![]()
)
G - moduł sztywności
γ - kąt odkształcenia postaciowego
Wartość kąta γ podajemy w mierze łukowej, a ponieważ jest to kąt mały, to:
γ ≈ tg γ
Wzór można więc napisać w postaci:
τ = G tg γ
2. Moduł sztywności
Moduł sztywności G liczbowo jest równy naprężeniu stycznemu τ, gdy ciało zostanie odkształcone o taki kąt γ, którego tg jest równy jedności.
Jednostką G jest ![]()
3. Wyprowadzenie wzorów roboczych
Czyste odkształcenie postaci obserwuje się podczas skręcenia np. drutu lub pręta o kształcie walca, którego górny koniec jest umocowany, a na dolny działa siła styczna, powodująca jego skręcenie o kąt ∆ φ.
Gdy odkształcenie jest sprężyste, ciało będzie wykonywało drgania obrotowe o okresie: (1)
![]()
Gdzie:
I-moment bezwładności ciała
D-moment kierujący
Moment kierujący D zależy od modułu sztywności G i geometrycznych wymiarów ciała: (2)
![]()
Podstawiając wartość D do wzoru, otrzymamy:
![]()
Widzimy, że okres drgań jest bezpośrednio związany z modułem sztywności G danego ciała. Powyższe wyrażenie posłuży nam do wyznaczania modułu sztywności G. Jednakże obliczenie momentu bezwładności I, który występuje we wzorze nie zawsze jest łatwe, często wręcz jest niemożliwe. Trudność tę możemy wyeliminować stosując następujący rachunek związany z ruchem balansowym układu (rys. 1). Mierzymy okresy drgań dla dwóch różnych momentów bezwładności krzyżaka. W ten sposób znajdujemy różnicę momentów bezwładności, która wystarcza do obliczenia modułu sztywności G.
rys. 1 rys. 2
Drut należy zamocować jednym końcem w uchwycie A, natomiast drugim - w uchwycie krzyżaka B. Jeżeli skręcimy krzyżak o pewien kąt, to na skutek sprężystości drutu krzyżak będzie wykonywał drgania w płaszczyźnie poziomej.
W celu zmiany momentu bezwładności wahadła stosujemy cztery ciężarki o jednakowych masach, które umieszczamy np. w odległości d1 od osi obrotu krzyżaka (rys.2) i dokonujemy pomiaru okresu T1 dla tego przypadku. Następnie umieszczamy ciężarki w odległości d2 i mierzymy okres T2.
W myśl wzoru nr 1 otrzymujemy dla obydwu przypadków następujące wzory na okres: (3)
![]()
oraz (4)
![]()
Moment bezwładności układu ciał jest sumą momentów bezwładności ciał tego układu, zatem:
I1=Ik + 4md12
I2=Ik + 4md22
Gdzie:
Ik - moment bezwładności samego krzyżaka,
4md12 - moment bezwładności czterech dodatkowych mas, umieszczonych w odległości d1,
4md22 - moment bezwładności czterech dodatkowych mas, umieszczonych w odległości d2.
Wyrażenia na I1 oraz I2 podstawiamy odpowiednio do równań (3) i (4).
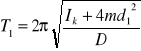
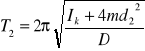
Z powyższych układów równań łatwo jest wyeliminować Ik. Podnosimy je do kwadratu i odejmujemy stronami (od drugiego pierwsze, gdyż T2>T1):
![]()
![]()
![]()
Podstawiając D (wzór 2) otrzymujemy:
![]()
![]()
stąd (5)
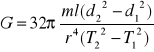
Korzystając ze wzoru (5), możemy obliczyć moduł sztywności materiału z którego jest zrobiony użyty drut.
II Opis ćwiczenia
Wykonanie pomiaru:
Wyznaczyć masę ciężarków i umieścić je na krzyżaku K w odległości d1.
Wprawić krzyżak w drgania skrętne i stoperem zmierzyć czas 20 okresów. Pomiar wykonać trzy razy i obliczyć średnią wartość okresu T1śr.
Zmienić położenie ciężarków ( na odległość d2) i zmierzyć okres T2śr jak w punkcie drugim.
Zmierzyć długość drutu miarką milimetrową oraz jego średnicę śrubą mikrometryczną.
Dane podstawić do wzoru (5) i obliczyć moduł sztywności.
Wyniki umieścić w zamieszczonej tabeli.
T1 |
T1śr |
T2 |
T2śr |
m |
l |
r |
G |
|
|
|
|
|
|
|
|
5
Wyszukiwarka
Podobne podstrony:
OGNIWA (2), Sprawozdania - Fizyka
Ćwiczenie nr 50b, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr50b
Mech- Badanie zależności współczynnika lepkości cieczy od te, Sprawozdania - Fizyka
Doświadczalne spr p. Malusa, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr70
Sprawozdanie Fizyka ćwiczenie 4(M04)
ćw13 sprawozdania fizyka 3, Sprawozdanie
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
Pomiar promieni krzywizny soczewki płasko - wypukłej, Sprawozdania - Fizyka
Ćwiczenie nr 82, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr82
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
Moment Bezwładności, Sprawozdania - Fizyka
Wyznaczanie momentu bezwładności brył za pomocą drgań skrę(1 (2), Sprawozdania - Fizyka
Ćwiczenie nr 65c, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65c
test metale tabela, Studia, Ogólne, Fiyzka, od romka, fizyka, sprawozdania fizyka
Bezwladnosc tab, Sprawozdania - Fizyka
Mech- Wyznaczanie ciepła topnienia lodu(1), Sprawozdania - Fizyka
Atom- Wyznaczanie stałej Plancka i pracy wyjścia elektronów(1), Sprawozdania - Fizyka
Sprawozdanie Fizyka ćwiczenie 6(O01)
więcej podobnych podstron