Zasady statyki więzy i ich reakcje.
1. Zasada równoległoboku - dwie siły przyłożone do jednego punktu możemy zastąpić siłą wypadkową, wyznaczoną jako przekątna równoległoboku zbudowaną na nich siłą
2. Dwie siły przyłożone do ciała sztywnego są w równowadze gdy działają wzdłuż jednej prostej i mają te same wartości, ale przeciwne zwroty. Układ taki nazywamy zerowym.
3. Działanie danego układu sił nie zmieni się, jeżeli dodamy bądź odejmiemy układ zerowy (układ sił równoważących)
4. Zasada zesztywnienia równowaga sił działających na ciało rzeczywiste nie zmieni się przez zesztywnienie tego ciała.
5. Każdemu działaniu towarzyszy równe co do wartości o przeciwnym zwrocie i leżące na tej samej prostej przeciwdziałanie.
6. Zasada oswobodzenia z więzów -. Aby oswobodzić ciało z więzów należy więzy zastąpić siłami zaznaczonymi przy pomocy wektorów
WIĘZY. REAKCJE WIĘZÓW
W przestrzennym układzie współrzędnych x, y, z ciało swobodne może przesuwać się wzdłuż osi x, y, z(trzy ruchy składowe) oraz może obracać się dookoła trzech osi (też trzy ruchy składowe). Tak, więc ciało swobodne ma 6 stopni swobody, gdyż w przestrzeni może wykonywać 6 ruchów składowych (trzy przesunięcia i trzy ruchy obrotowe). Aby oswobodzić ciało z więzów należy więzy zastąpić siłami zaznaczonymi przy pomocy wektorów
Rodzaje więzów:
- Podpory ruchome. Należy do nich: łożysku ruchomym. Reakcja podpory ruchomej jest zaczepiona w punkcie styczności ciała z podporą i ma zawsze kierunek prostopadły do powierzchni podpieranej (niezależnie od kierunków sił działających na ciało podpierane). Podporę ruchomą oznaczamy schematycznie za pomącą trójkąta równobocznego dodatkowo podkreślonego linią, która przedstawia powierzchnię podpierająca.
- Więzy wiotkie Ciegno. Zaliczamy tu sznury, liny, łańcuchy itp. Siła w takich więzach jest zawsze skierowana wzdłuż lini cięgna. Cięgno zastępujemy odpowiednią siłą reakcji tego cięgna. Siła rozciągająca od węzła na zewnątrz .
- Podpora stała. Tego rodzaju więzy uniemożliwiają przesunięcie ciała, lecz umożliwiają obrót wokół punktu podparcia.
-Zamurowanie- utwierdzenie jednym końcem uniemożliwia ruch zarówno obrotowy jak i przesuwny charakteryzują go dwie wielkości reakcja utwierdzenia oraz moment utwierdzenia
2.Udowodnij tw. Varignon'a
Moment siły wypadkowej względem dowolnego punktu na płaszczyźnie Jest równy sumie momentów sił składowych względem tego samego punktu
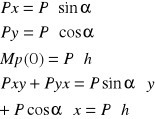
3. Para sił def.
Para sił to układ sił równoległych co do wartości lecz zwrotach przeciwnych, działających wzdłuż prostych równoległych przesuniętych o pewną odległość.
Własności
Pao1-Pbo1=P(ao1-bo1)=Ph
Pao2-Pbo2=P(ao2-bo2)=Ph
4.Tw o 3 siłach
Jeżeli na płaskim układzie sziałają 3 siły nierównoległe to może on znajdować się w równowadze tylko wtedy gdy linie działania tych sił przecinają się w jednym punkcie, a same siły tworzą zamknięty trójkąt sił.
5 Tarcie poślizgowe(posuwiste)-zasady tarcia
Siła tarcia zmienia się w zależności od tego jak zmienia się siła zew P , która chce spowodować względny ruch ciała względem powierzchni styku na której leży ciało (lub względem innego ciała).Siła tarcia zawsze będzie przeciwdziałała temu ruchowi .Wzrost siły tarcia T spowodowany wzrostem siły zewnęcznej P jest możliwy tylko do pewnej granicznej wartości tarcia ( T max) Dalszy wzrost siły P spowoduje już naruszenie stanu równowagi i ciało zacznie się przesuwać
![]()
u - zależy od rodzaju powierzchni stykających się powierzchni.
ZASADY TARCIA
1.Siła Tarcia nie zależy od wielkości stykających się powierzchni a jedynie od ich stanu ( czy powierzchnia jest z tego samego materiału , czy jest chropowata czy słucha )
2. Siła tarcia dla ciała znajdującego się w spoczynku może zmieniać się od 0 do wartości max zwanym tarciem całkowicie rozwiniętym zależnym od nacisku normalnego.
3.Dla ciała będącego w ruchu siła, która jest potrzebna do kontynuacji ruchu jest mniejsza od siły która ja wywołuje.
4. Siła tarcia ma zawsze zwrot przeciwny do zamierzonego kierunku względnego.
6. Opór tarcia przy toczeniu:
a)kula o promieniu r i ciężarze G spoczywa na płaszczyźnie
b)jeżeli do osi kuli przyłożymy poziomą siłę P wywoła to powstanie w miejscu styku kuli siły tarcia T , które zgodnie z warunkami równowagi musi być równa sile P .Suma momentów tych sił względem dowolnego punktu była równa zero .
T=N*f/r
współczynnik f - współczynnik tarcia przy toczeniu
7. Warunki równowagi płaskiego układy sił
Aby układ zostały równowadze suma algebraiczna rzutów na każdą z nierównoległych osi równać musie się 0 i suma momentu sił względem dowolnego punktu też musi równać się 0
8. Moment siły względem osi
Momentem siły względem osi nazywamy moment rzutu tej siły na płaszczyznę prostopadłą do osi - względem punktu przecięcia się osi z płaszczyzną.
Moment siły względem osi jest równy zeru wtedy, gdy siła i oś leżą w jednej płaszczyźnie.
9. Warunki równowagi dowolnego przestrzennego układu sił
Ciało obciążone dowolnym przestrzennym układem sił będzie w równowadze, gdy będzie spełnionych sześć następujących warunków równowagi:
suma algebraicznych rzutów wszystkich sił na oś x musi być równa zeru, czyli Σ P i x = 0;
suma algebraicznych rzutów wszystkich sił na oś y musi być równa zeru, czyli Σ P i y = 0;
Suma algebraicznych rzutów wszystkich sił na oś z musi być równa zeru, czyli Σ P i z = 0;
Suma algebraicznych wszystkich sił względem osi x musi być równa zeru, czyli Σ M i x = 0;
Suma algebraicznych wszystkich sił względem osi y musi być równa zeru, czyli Σ M i y = 0;
Suma algebraicznych wszystkich sił względem osi z musi być równa zeru, czyli Σ M i z = 0.
10.Wyznaczenie wypadkowej układu sil równoległych
wypadkowa dwóch sił równoległych o zgodnych zwrotach jest równa sumie algebraicznej wartości sił składowych , jest do nich równoległa , a jej punkt przyłożenia dzieli wew. Odcinek między punktami przyłożenia sił składowych w stosunku odwrotnie proporcjinalnym do wartości tych sił
11. Środki cięszkości Brył powiężchni i lini
- jeżeli ciało ma jedną oś symetrii, to środek ciężkości leży na tej osi,
- jeżeli ciało ma dwie (lub więcej) osie symetrii, to środek ciężkości leży na przecięciu się tych osi,
- jeżeli ciało ma środek symetrii, to punkt ten jest równocześnie środkiem ciężkości
- środek ciężkości ciała złożonego z kilku ciał pokrywa się z środkiem ciężkości punktów materialnych leżących w środkach poszczególnych ciał składowych, przy czym masy tych punktów są równe masom poszczególnych ciał składowych.
13. Tw Guldina-Pappusa zastosowanie
I twierdzenie Pappusa-Guldina - powierzchnia zakreślona przez obrót odcinka linii płaskiej około osi leżącej na płaszczyźnie tej linii i nie przecinającej jej równa jest iloczynowi długości jej przez długość łuku, jaką zatacza przy obrocie środek masy tej linii ![]()
gdzie xC - odległość środka masy linii od osi Oy
II twierdzenie Pappusa-Guldina - objętość bryły zatoczonej przez obrót figury płaskiej dookoła osi leżącej na płaszczyźnie figury i nie przecinającej go, równa się iloczynowi powierzchni figury przez długość drogi, jaką zatacza środek masy figury ![]()
1
Wyszukiwarka
Podobne podstrony:
WYTRZYMAOsc sciga, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV mechanika i wytrzymał
TEMATY EGZAMINACYJNE Z PBU pwsz ioś kalisz, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś,
Projekt 09, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 07, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 005, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc mater
Projekt 03, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 04, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 02, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Projekt 01, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, IV odpady i wytrzymalosc materi
Statyka1, inżynieria ochrony środowiska kalisz, Rok 1 IOS, Mechanika budowli, Mechanika budowli - pr
Przedsiebi, inżynieria ochrony środowiska kalisz, z mix inżynieria środowiska moje z ioś pwsz kalis
pwsz ioś kalisz Ćw. 6 POLARYMETRIA, inżynieria ochrony środowiska kalisz, a pwsz kalisz ioś, analiza
więcej podobnych podstron