Laboratorium Podstaw Fizyki
Æwiczenie B-2	Temperaturowa zale¿noœæ opornoœci elektrycznej metalu i pó³przewodnika.
Wydzia³ : FTiMS	Semestr: 2	Rok akademicki : 1993/94	Dzieñ tygodnia: œroda	Data : 11.05.1994
Zespó³ nr 1	Ocena	Przygotowanie	Sprawozdanie	Zaliczenie
1.Krzysztof Góral
2.S³awomir Matyjaœkiewicz
Prowadz¹cy : dr Chendor

1.Podstawy fizyczne .

Cech¹ charakterystyczn¹ cia³ sta³ych jest fakt, i¿ s¹ one zbudowane z gêsto u³o¿onych atomów powi¹zanych ze sob¹ si³ami chemicznymi w taki sposób, ¿e niemo¿liwe s¹ wzglêdne przemieszczenia (miêdzy innymi to w³aœnie odró¿nia cia³a sta³e od cieczy oraz gazów). Atomy w ciele sta³ym u³o¿one s¹ periodycznie tworz¹c sieæ krystaliczn¹. Z punktu widzenia mechaniki kwantowej tworz¹ one jeden uk³ad, w którym g³ówn¹ rolê graj¹ si³y culombowskie. Wp³yw warunków zewnêtrznych jest znamienny jedynie w przypadku elektronów walencyjnych - ulegaj¹ one silnym oddzia³ywaniom culombowskim ze strony s¹siednich atomów, co powoduje zmianê ich stanów kwantowych. To w³aœnie te elektrony decyduj¹ w g³ównym stopniu o w³aœciwoœciach cia³ sta³ych.

Mo¿na zatem zastosowaæ przybli¿enie jednoelektronowe oraz ograniczyæ siê w rozwi¹zywaniu problemu jedynie do ruchu elektronów walencyjnych.

Równanie Schrodingera po zastosowaniu wymienionych przybli¿eñ daje w wyniku funkcje falowe w postaci fal p³askich modulowanych funkcjami Blocha:

gdzie r jest wektorem po³o¿enia, zaœ k wektorem falowym, natomiast kwadrat wielkoœci okreœla prawdopodobieñstwo znalezienia elektronu.

Z rozwi¹zania funkcji falowych wynika istnienie pewnych przedzia³ów energii dozwolonych dla elektronów zwanych pasmami dozwolonymi, natomiast zakresy energi nie dozwolonych dla elektronów nosz¹ nazwê pasm zabronionych. Obszary pasm dozwolnych sk³adaj¹ siê z wielkiej liczby poziomów energetycznych obsadzanych zgodnie z zakazem Pouliego w kolejnoœci zgodnej ze wzrostem energii, a¿ do poziomu energetycznego zwanego energi¹ Fermiego. W temperaturze 0K wszystkie stany poni¿ej tej energi s¹ wype³nione.

Bior¹c pod uwagê w³aœciwoœci elektryczne mo¿na wyró¿niæ dwa pasma energetyczne: pasmo walencyjne i pasmo przewodnictwa . Poziom Fermiego mo¿e znajdowaæ siê wewn¹trz pasma energetycznego (metale) lub w obszarze przerwy energetycznej (pó³przewodniki i izolatory).

Dla matalu pasmo przewodnictwa jest wype³nione elektronami tylko czêœciowo. Dla czystego pó³przewodnika w temperaturze 0K pasmo walencyjne jest wype³nione czêœciowo. W izolatorach z kolei przerwa energetyczna jest na tyle du¿a, ¿e energia ruchu cieplnego nie jest wystarczaj¹ca na przeniesienie elektronów do pasma przewodnictwa.

Klasyczny obraz przewodnictwa elektrycznego w metalach .

Periodyczna sieæ krystaliczna w metalach wype³niona jest gazem elektronowym (elektronami walencyjnymi poruszaj¹cymi siê w chaotycznym ruchu cieplnym, oderwanymi od rodzimych atomów si³ami culobowskimi). W zewnêtrznym polu elektrycznym na elektrony dzia³a si³a:

Wzrost prêdkoœci unoszenia ograniczony jest przez ci¹g³e zderzenia elektronów z jonami sieci, których efekty mo¿na opisaæ :

Wypadkowy ruch elektronów pod wp³ywem obu tych si³ opisuje równanie:

Ostatecznie prêdkoœæ przyjmuje wartoœæ sta³¹ zwan¹ prêdkoœci¹ dryfu:

Gêstoœæ pr¹du definiuje wzór:

Korzystaj¹c z zale¿noœci na ruchliwoœæ noœników pr¹du oraz na przewodnoœæ pr¹du elektrycznego otrzymujemy wzór na prawo Ohma :

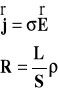
Chocia¿, obliczenia przewodnictwa dla metali przeprowadzone w ramach fizyki klasycznej daj¹ dobr¹ zgodnoœæ z doœwiadczeniem, to jednak nie pozwala model klasyczny na wyt³umaczenie m.in. zjawisk pó³przewodnictwa i nadprzewodnictwa.

Kwantowy opis przewodnictwa metali .

Gdyby atomy w kryszta³ach u³o¿one by³y idealnie periodycznie to zgodnie z mechanik¹ kwantow¹ fale elektronowe nie by³y by rozpraszane w swoim ruchu i materia³ posiada³by zerowy opór elektryczny. W rzeczywistych przewodnikach istniej¹ pewne niedoskona³oœci, takie jak drgania sieci (fonony), defekty sieci krystalicznej powoduj¹ce, silne rozpaszanie fal elektronowych - opór elektryczny.

Wed³ug interpretacji kwantowej czynny udzia³ w przewodnictwie bior¹ jedynie elektrony znajduj¹ce siê w pobli¿u poziomu Fermiego, elektrony znajduj¹ce siê poni¿ej tej energii bior¹ jedynie bierny udzia³ w przep³ywie pr¹du elektrycznego.

Temperaturowa zale¿noœæ opornoœci elektrycznej metali .

Koncentracja n noœników pr¹du elektrycznego w metalach jest niezale¿na od temperatury. Zatem wielkoœci¹ okreœlaj¹c¹ zale¿noœæ opornoœci metalu od temperatury jest ich ruchliwoœæ, a w³aœciwie temperaturowa zale¿noœæ czasu relaksacji .

Dlatego opornoœæ w modelu klasyczny powinna zale¿eæ od temperatury:

W modelu kwantowym natomiast przybiera ona inn¹ postaæ:

a w temperaturach bardzo niskich:

Rozpraszanie na defektach i domieszkach jest niezale¿ne od temperatury.

Przewodnictwo elektryczne pó³przewodników .

W pó³przewodnikach w temperaturze wy¿szej od 0K istniej¹ dwa pasma czêœciowo zape³nione, w których mo¿e nastêpowaæ transport elektronów - przy czym mo¿na mówiæ o dwu rodzajach przewodnictwa: elektronowym i dziurowym. Takie pó³przewodniki nazywane s¹ samoistnymi - jedynym ¿ród³em noœników pr¹du s¹ dla nich przejœcia elektronów z pasma walencyjnego do pasma przewodnictwa.

Przewodnoœæ elektryczn¹ przewodnika okreœla wzór:

gdzie n i s¹ odpowiednio koncentracj¹ i ruchliwoœci¹.

Koncentracja uzale¿niona jest od wzrostu temperatury zale¿noœci¹:

Temperaturowa zale¿noœæ oprnoœci elektrycznej pó³przewodnika .

Temperaturowa zale¿noœæ ruchliwoœci noœników w pó³przewodniku jest zaniedbywalna, a wiêc czynnikiem decyduj¹cym o zmianach oporu ze zmian¹ temperatury jest koncentracja noœników pr¹du. Temperaturow¹ zale¿noœæ przewodnoœci elektrycznej pó³przewodnika opisuje wzór:

2.Cel æwiczenia .

Celem æwiczenia jest zbadanie temperaturowej zale¿noœci opornoœci elektrycznej metalu (miedzi) i pó³przewodnika (termistora) oraz ukazanie charakterystycznych cech tej zale¿noœci dla obu rodzajów materia³ów. Dla porównania zbadano równie¿ tak¹ zale¿noœc dla stopu oporowego (konstantanu).

3.Przebieg æwiczenia i opracowanie wyników pomiarowych.

Dokonano serii pomiarów oporu elektrycznego miedzi, termistora i konstantanu w zale¿noœci od temperatury (skok co 5C) dla ogrzewania i ch³odzenia. Wyniki zamieszczone s¹ w protokole .

Nastêpnie, korzystaj¹c z zale¿noœci R=R0(1+t) (gdzie t=T-T0 jest temperatur¹ w skali Celsjusza), z metody najmniejszych kwadratów uzyskano nastêpuj¹ce wyniki:

dla ogrzewania a=R0=0,0237471 Sa=R0S=0,0003711

b=R0=6,061254 Sb=0,016093

dla ch³odzenia a=0,0294644 Sa=0,0009212

b=6,18787 Sb=0,03922

Po wykonaniu prostych przekszta³ceñ (=a/R0 oraz S=Sa/R0)obliczono temperaturowy wspó³czynnik opornoœci dla miedzi (osobno dla ogrzewania i ch³odzenia) oraz jego b³¹d. Uzyskano nastêpuj¹ce wyniki:

dla ogrzewania = 0,0039 [1/C] S = 0,0001 [1/C]

dla ch³odzenia = 0,0037 [1/C] S = 0,0002 [1/C]

Po uœrednieniu otrzymujemy: = 0,0038 0,0001 [1/C]

Z kolei, korzystaj¹c z zale¿noœci
(gdzie: k-sta³a Boltzmana, T-temperatura w skali Kelvina), z metody najmniejszych kwadratów uzyskano nastêpuj¹ce wyniki:

dla ogrzewania a=E/2k=3840,112 Sa=SE /2k=18,673

b=lnR0=-1,324 Sb=0,056 dla ch³odzenia a=3686,462 Sa=SE /2k=72,197

b=-0,903 Sb=0,219

Po wykonaniu prostych przekszta³ceñ (k=1,38110-23, E=2ka, SE =2kSa) obliczono energiê jonizacji domieszek w pó³przewodniku (osobno dla ogrzewania i ch³odzenia) oraz jej b³¹d. Uzyskano nastêpuj¹ce wyniki:

dla ogrzewania E = 0,66 eV SE = 0,01 eV

dla ch³odzenia E = 0,64 eV SE = 0,01 eV

Po uœrednieniu otrzymujemy: E = 0,65 0,01[eV]

Na wykresach nie zaznaczono b³êdów, poniewa¿ by³y one znikomo ma³e w porównaniu ze skal¹ u¿ytej podzia³ki.

4.Wnioski.

Temperaturowy wspó³czynnik opornoœci dla miedzi jest nieco mniejszy dla ch³odzenia (wolniejszy spadek oporu wraz z temperatur¹) - mo¿na ten fakt zinterpretowaæ jako swoist¹ 'bezw³adnoœæ' materia³u. Wykresy zale¿noœci oporu od temperatury dla termistora przypominaj¹ wyraŸnie wyk³adnicze malenie. Konstantan wykazuje ma³e, choæ zauwa¿alne zmiany oporu wraz z temperatur¹. Energia jonizacji jest porównywalna z przerw¹ energetyczn¹ dla pó³przewodnika (kilka dziesi¹tych elektronowolta).

---