TESTY DLA DWÓCH GRUP PORÓWNAWCZYCH - ZMIENNA ZALEŻNA PORZĄDKOWA, DANE NIEZALEŻNE: TEST U-Manna-Whitneya

- testu U Mann-Whitneya używamy jeśli:

(1) mamy do czynienia z dwiema grupami porównawczymi, na przykład, chcemy porównać jaka jest różnica pomiędzy kobietami i mężczyznami (dwie grupy porównawcze) pod względem wykształcenia

(2) zmienna zależna jest wyrażona co najmniej na skali porządkowej (bazując na przykładzie powyżej, zmienna zależna to wykształcenie, które może być wyrażone na skali: podstawowe, zawodowe, średnie, wyższe); oczywiście przy pomocy testu U Manna-Whitneya można również testować zmienne wyrażone na skalach mocniejszych niż porządkowa (na przykład zmienną wyrażoną na skali Likerta (a zatem zmienną interwałową), powiedzmy ocena produktu na skali: dobrze - raczej dobrze - ani dobrze, ani źle - raczej źle - źle), lepiej jest jednak zawsze jeśli to tylko możliwe stosować testy parametryczne.

(3) porównywane grupy są niezależne, z porównaniami niezależnymi mamy do czynienia zawsze wtedy, kiedy grupy nie są w żaden sposób ze sobą powiązane, łatwiej jest opisać grupy niezależne poprzez… charakterystykę grup zależnych; grupy zależne są w jakiś sposób ze sobą powiązane, na przykład mąż i żona; rodzic i dziecko, brat i siostra, częściej jednak mamy do czynienia z grupami zależnymi w przypadku badania typu pretest - posttest; powiedzmy, że mamy grupę 30 osób, które badamy ze względu na odporność na stres przed zaaplikowaniem jakiegoś środka (pretest - `pierwsza' grupa), następnie aplikujemy ów środek i badamy te same osoby, tak by sprawdzić jak zmieniła się ich odporność na stres (posttest - `druga' grupa). Mamy zatem dwie grupy porównawcze (grupa przed i grupa po), o takich grupach i uzyskiwanych od tych grup danych mówimy, że są to grupy/ dane zależne - bo wyniki pochodzą od tych samych osób, w jakiś sposób są, więc od siebie zależne. Jeśli natomiast chcielibyśmy zbadać, jak jest reakcja kobiet i mężczyzn na dany środek i te 30 osób podzielilibyśmy na dwie grupy (kobiety i mężczyźni), a następnie dokonali pomiarów w tych dwóch grupach, to wówczas mielibyśmy do czynienia z danymi niezależnymi - bo wyniki w grupie kobiet i mężczyzn w żaden sposób nie są ze sobą powiązane. I w takim przypadku możemy posłużyć się testem U Manna-Whitneya!

Przypuśćmy następującą sytuację:

1. mamy skalę od 1 do 8, na której zakodowano wykształcenie, gdzie:

1. podstawowe

2. gimnazjalne

3. niepełne średnie

4. średnie

5. niepełne wyższe

6. licencjackie

7. wyższe

8. doktoranckie

2. mamy dwie grupy zawodowe (1) rolników i (2) pracowników umysłowych

3. w toku badań tych dwóch grup zawodowych uzyskano następujące wyniki:

ROLNICY	UMYSŁOWI
4	5
3	6
3	7
2	5
5	7
3	7
6	6
3	7

Na pierwszy rzut oka widzimy, że poziom wykształcenia w grupie rolników jest niższy niż w grupie pracowników umysłowych

Aby móc powiedzieć, iż te różnice są istotne statystycznie (nie są dziełem przypadku) musimy przeprowadzić test U Manna-Whitneya

W tym celu:

1. musimy obserwacją przypisać rangi, aby móc przypisać im rangi musimy wszystkie obserwacje `ustawić' w szeregu od najmniejszej do największej:

wartość	2	3	3	3	3	4	5	5	5	6	6	6	7	7	7	7
pozycja	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
ranga	1	3,5	3,5	3,5	3,5	6	8	8	8	11	11	11	14,5	14,5	14,5	14,5

2. dalsze obliczenia bazują na rangach, nie na wartościach

3. tworzymy zatem nową tabele, zamiast wartości wpisując rangi i

4. od razu obliczamy też sumę rang dla każdej grupy!

	ROLNICY (n=8)	UMYSŁOWI (n=8)
	6	8
	3,5	11
	3,5	14,5
	1	8
	8	14,5
	3,5	14,5
	11	11
	3,5	14,5
SUMA	40	96

5. kolejny etap to obliczenie statystyk U₁ i U₂ dla każdej z porównywanych grup, korzystamy ze wzorów:







gdzie:

n₁ - liczebność pierwszej grupy

n₂ - liczebność drugiej grupy

R₁ - suma rang w pierwszej grupie

R₂ - suma rang w drugiej grupie


= 60


= 4

6. wybieramy zawsze niższą wartość U, w naszym przypadku jest to U₂ = 4

7. sprawdzamy w tablicach z wartościami krytycznymi U czy wartość równa 4 pozwala na przyjęcie hipotezy alternatywnej, czyli czy pozwala stwierdzić, iż zaobserwowana prawidłowość (różnice pod względem wykształcenia) nie jest dziełem przypadku. Okazuje się, że wartość U równa 4 pozwala nam na stwierdzenie, że istnieje szansa mniejsza niż 1% na to, że zaobserwowana różnica jest dziełem przypadku.

Zaobserwowane przez nas różnice są istotne statystycznie na poziomie £ < 0,01

Uwaga! Przypadku odczytywania wartości krytycznych U, postępujemy inaczej niż w przypadku odczytywania wartości krytycznych chi-kwadrat! Odwołując się do przykładu powyżej, uzyskana przez nas wartość U=4 powinna być mniejsza niż wskazywane przez tablice wartości 13 (dla £ < 0,05) i 7 (dla £ < 0,01). W przypadku wartości krytycznych chi-kwadrat chodziło o to, żeby je `przekroczyć', tu chodzi o to by wartość U nie przekroczyła wartości krytycznych podanych w tablicach!

Uwaga! Jeśli mniejsza wartość obliczona (w naszym przypadku było to U₂ = 4) jest równa wartości z tablicy (w naszym przypadku były to wartości 13 i 7), to hipotezą zerową odrzucamy, czyli zależność (zaobserwowane różnice) jest istotna statystycznie! Innymi słowy jeśli wartość obliczone jest równa tej z tablicy to jest OK!

Uwaga!!! Jeśli którakolwiek z grup porównawczych ma liczebność większą niż 20, to statystykę testową U obliczamy ze wzoru:




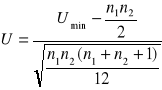
obszar krytyczny przyjmuje dla poziomu α=0,05 postać D : (-∞;-1,96>∪<1,96;+ ∞).

ZADANIA

W pewnym eksperymencie, w którym starano się poznać preferencje kobiet i mężczyzn odnośnie oglądanych programów/audycji telewizyjnych, poproszono o uszeregowanie sześciu typów programów/audycji TV w kolejności od tego, który lubi się najbardziej (wartość 1) do tego, który lubi się najmniej (wartość 6).

Badano następujące typy programów TV:

1. programy o tematyce publicystycznej

2. programy o tematyce kulinarnej

3. filmy fabularne

4. programy informacyjne

5. teleturnieje

6. programy sportowe

W przypadku teleturniejów otrzymano następujące wyniki (każda cyfra odzwierciedla miejsce, jakie zostało przypisane teleturniejom przez respondenta, pośród innych programów/ audycji TV):

KOBIETY (n=10)	MĘŻCZYZNI (n=10)
5	2
4	3
4	2
6	1
3	1
2	4
4	5
4	4
3	2
4	3

Proszę sprawdzić czy istnieją istotne statystycznie różnice pomiędzy kobietami i mężczyznami pod względem częstości oglądania/lubienia teleturniejów?

W przypadku programów publicystycznych otrzymano następujące wyniki (każda cyfra odzwierciedla miejsce, jakie zostało przypisane programom publicystycznym, przez respondenta, pośród innych programów/ audycji TV):

KOBIETY (n=10)	MĘŻCZYZNI (n=10)
2	4
3	3
4	4
6	6
1	3
2	4
4	5
2	4
3	6
2	6

Proszę sprawdzić czy istnieją istotne statystycznie różnice pomiędzy kobietami i mężczyznami pod względem częstości oglądania/lubienia programów publicystycznych?

str. 1

---