Wyznaczenie parametrów wytrzymałości na ścinanie. Parametry wytrzymałości całkowitej: ϕu, cu oraz parametry wytrzymałości efektywnej ϕ′, c′.

I Część teoretyczna.

Opór tarcia w odniesieniu do jednostki powierzchni ścinania gruntów niespoistych w stanie równowagi granicznej wyraża się wzorem Coulomba:

t = τ = σn * f = σn tg Φ

Dla gruntów spoistych, mających opór tarcia i spójności, wzór będzie miał postać:

t = τ = σ_n tg Φ + C

gdzie: t - opór tarcia wewnętrznego i spójności, (Pa)

τ - naprężenie ścinające, (Pa)

f = tg Φ - współczynnik tarcia wewnętrznego

Φ - kąt tarcia wewnętrznego w stopniach

σ_n - naprężenie normalne do powierzchni ścięcia, (Pa)

C - spójność, (Pa)

Aby nastąpiło ścięcie naprężenia ścinające muszą być większe od oporu tarcia wewnętrznego

i spójności (wytrzymałości gruntu na ścinanie): τ > t

Na podstawie powyższych wzorów można stwierdzić, że wytrzymałość na ścinanie

jest funkcją współczynnika tarcia wewnętrznego, oraz spójności i naprężenia normalnego do płaszczyzny ścinania

Wytrzymałość gruntu na ścinanie jest to maksymalny opór jednostkowy jaki stawia

grunt naprężeniom ścinającym w chwili nastąpienia ścięcia. Określenie wytrzymałości gruntu na ścinanie sprowadza się do określenia kąta tarcia wewnętrznego i spójności.

Laboratoryjnie kąt tarcia wewnętrznego i spójności gruntu wyznacza się za pomocą:

1. aparatu bezpośredniego aparatu ścinania (skrzynkowego)

2. aparatu trójosiowego ściskania

Oznaczenie wytrzymałości na ścinanie za pomocą aparatu bezpośredniego ścinania.

Do badania należy używać próbek w stanie najbardziej zbliżonym do stanu w jakim grunt będzie pracował w naturze. Próbki do badań powinny być tak pobrane aby płaszczyzna ścinania była równoległa do powierzchni terenu w miejscu ich zalegania w podłożu.

Ścięcia próbki należy dokonać po osiągnięciu stabilizacji osiadań (po zakończeniu osiadania

przy danym stopniu obciążenia). Pomiar osiadania próbki gruntu przeprowadza się do czasu, gdy różnica dwóch ostatnich odczytów czujnika nie przekracza 0,002 mm. Jeżeli potrzeby obliczeń statycznych nie podają innych warunków, to stosujemy dodatkowe obciążenie wynoszące 100, 150, 200, 300 i 400 kPa ( 1,0 1,5 2,0 3,0 i 4,0 kG/cm )

Ścinanie próbek wykonujemy jedną z dwóch metod:

1. M. Podstawową - prędkość przemieszczania nie przekracza 0,05 mm/min

1. M. Przybliżoną - prędkość przemieszczenia mieści się w granicach 0,5 - 1,2 mm/min.

Siłę ścinającą przypadającą na jednostkę powierzchni obliczamy z wielkości odkształcenia pierścienia dynamometru, skali pierścienia dynamometru i pola powierzchni ścięcia stosując wzór

τf = =

w którym: τ_f - wytrzymałość próbki na ścinanie (Pa)

a - wielkość odkształcenia pierścienia dynamometru w zakresie 0 - 1 mm.

b - skala dynamometru

Q_max - największa wartość siły ścinającej (N)

F - pole płaszczyzny ścięcia próbki gruntu (cm²)

W przypadku odkształcenia dynamometru większego niż jeden milimetr, lecz mniejszego niż dwa, wzór na naprężenie ścinające będzie miał postać :

τ_f = =

gdzie: b - siła wyw. odkształcenie pierścienia dynamometru równe 1 mm (N)

a' - wielkość odkształcenia pierścienia dynamometru powyżej 1 mm

b' - skala pierścienia dynamometru ( różnica siły wywołującej odkształcenia pierścienia dynamometru w zakresie od 2 do 1 mm (N/mm)

F - pole płaszczyzny ścięci próbki

W przypadku, gdy Qmax nie występuje, siła Q natomiast wzrasta w sposób ciągły wraz ze wzrostem wzajemnego przesunięcia skrzynek, wówczas jako wartość τf należy przyjąć wartość naprężenia odpowiadającego przesunięciu skrzynek równemu 10% długości boku próbki.

`Naprężenia normalne, przypadające na jednostkę powierzchni, obliczamy dzieląc obciążenie przez pole powierzchni obciążanej próbki, która w aparacie bezpośredniego ścinania równa się polu powierzchni ścięcia próbki:

σ_n =

w którym: σ_n - naprężenie normalne, (Pa)

P - obciążenie próbki, równe sumie obciążenia wstępnego i dodatkowego (N)

F - pole poziomego przekroju próbki równe polu płaszczyzny ścięcia (cm²)

Graficznie kąt tarcia wewnętrznego i spójność badanego gruntu wyznacza się nanosząc uzyskane wyniki na prostokątny układ współrzędnych. Wartości kąta tarcia wewnętrznego i spójności przyjmuje się z wykresu wykonanego na podstawie wyników przeprowadzonych badań.

Gdy dysponujemy wynikami σn i τf uzyskanymi z badań laboratoryjnych, możemy

wyznaczyć kąt tarcia wewnętrznego Φu i spójność Cu za pomocą zasady aproksymacji liniowej, metodą najmniejszych kwadratów:

Φu = arctg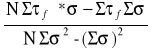

Cu =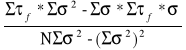

gdzie: τ_f - wartość wytrzymałości (oporu) gruntu na ścinanie, (Pa)

σ - całkowite obciążenie jednostkowe próbek, (Pa)

N - liczba uwzględnionych punktów na wykresie

Średnie odchylenie kwadratowe wytrzymałości na ścinanie (Sτf) obliczamy ze wzoru:

Sτ_f =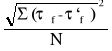

w którym: τ_f - wartość wytrzymałości (oporu) gruntu na ścinanie, (Pa)

N - liczba uwzględnionych punktów na wykresie

τ'_f - wartość wytrzymałości gruntu na ścinanie, (Pa) określona ze wzoru:

τ'_f = σ tg Φ_u + Cu

W przypadku, gdy oznaczenia kąta tarcia wewnętrznego i spójności przeprowadzamy

w aparacie trójosiowego ściskania z pomiarem ciśnienia parowego, to naprężenia panujące w gruncie można wyrazić w naprężeniach efektywnych określonych wzorem:

σ_n' = σ_n - u

gdzie: σ_n' - efektywne naprężenia normalne, (Pa)

σ_n - naprężenia normalne (całkowite), (Pa)

u - ciśnienie porowe, (Pa)

Naprężenie efektywne σn' - jest to ta część jednostkowego obciążenia normalnego

którą przyjmuje szkielet gruntowy

Ciśnieniem porowym u - nazywa się tę część jednostkowego obciążenia, którą przyjmuje woda znajdująca się w porach gruntu

Uwzględniając efektywne naprężenia normalne i ciśnienie porowe, wzór na opór gruntu na ścinanie będzie miał postać:

τ_f = σ_n' tg Φ' + c'

gdzie: τ_f - opór gruntu na ścinanie, (Pa)

σ_n' - efektywne naprężenia normalne (σ' = σ - u), (Pa)

c' - spójność efektywna, (Pa)

---