Bartosik |
Radosław |
Borejszo |
Aron |
Burmann |
Piotr |
Ciania |
Piotr |
Grochowalski |
Robert |
Kowalczyk |
Piotr |
Najder |
Dariusz |
Parol |
Piotr |
Pietrzyk |
Rafał |
Woźniak |
Tomasz |
Rodziewicz |
Łukasz |
Imię i nazwisko ............................................................................................ Data
Jeżeli a i b są wartościami dokładnymi,
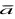
i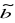
ich przybliżeniami , a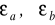
błędami względnymi, to błąd względny różnicy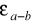
:
może być duży mimo małych
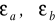
jeżeli a-b jest małe TAK / NIE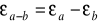
TAK / NIEjest stosunkiem przybliżonej wartości różnicy do wartości dokładnej TAK / NIE
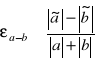
TAK / NIE
Układ równań normalnych występujący przy rozwiązaniu zadania aproksymacji liniowej, średniokwadratowej:
jest układem równań liniowych TAK / NIE
jest łatwy do rozwiązania gdy funkcje bazowe są rodziną funkcji ortogonalnych TAK / NIE
jest układem równań różniczkowych liniowych TAK / NIE
jest zbiorem skalarnych równań niezależnych gdy węzły aproksymacji są różne TAK / NIE
Dla dowolnych różnych n+1 punktów węzłowych (xi, fi) i=0,1,...,n :
istnieje dokładnie jeden wielomian interpolacyjny P(x) stopnia n taki, że P(xi)=fi, i=0,1,...,n TAK / NIE
istnieją dwa różne wielomiany interpolacyjne stopnia n, które można wyznaczyć a)metodą rodziny trójkątnej, b) metodą Lagrange'a TAK / NIE
istnieje nieskończenie wiele wielomianów interpolacyjnych stopnia n różniących się o stałą TAK / NIE
istnieje wielomian interpolacyjny spełniający wzór Lagrange'a:
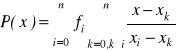
TAK / NIE
Złożona kwadratura trapezów
powstała przez całkowania wielomianu interpolacyjnego stopnia 2 na przedziale [a, b] TAK / NIE
ma rozwinięcie błędu zawierające tylko parzyste potęgi długości kroku TAK / NIE
jest podstawą metody całkowania Romberga TAK / NIE
jest pomocna w metodzie różniczkowania przy pomocy różnicy progresywnej TAK / NIE
Metoda Newtona rozwiązująca równanie f(x)=0
jest metodą iteracyjną TAK / NIE
ma równanie iteracji
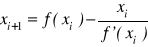
TAK / NIEjest szybciej zbieżna od metody siecznych TAK / NIE
jest zbieżna z kwadratem dla zer wielokrotnych TAK / NIE
Metoda Lehmera-Schura
jest zawsze zbieżna TAK / NIE
jest szybciej zbieżna od metody Bairstowa TAK / NIE
wyznacza tylko rzeczywiste zera wielomianu TAK / NIE
korzysta z kryterium obecności zera w kole jednostkowym TAK / NIE
Metoda eliminacji Gausa
jest metodą iteracyjną TAK / NIE
pozwala na wyznaczenie rozkładu trójkątnego macierzy TAK / NIE
sprowadza układ równań liniowych do postaci trójkątnej TAK / NIE
pozwala obliczyć wyznacznik macierzy TAK / NIE
Metoda QR obliczania wartości własnych
jest modyfikacją metody eliminacji Gausa, której autorami są Quark i Romberg TAK / NIE
wykorzystuje rozkład macierzy na macierz ortogonalną i trójkątną górną TAK / NIE
może być stosowana tylko dla macierzy symetrycznych TAK / NIE
oblicza wartości własne korzystając z iteracyjnego przekształcania przez podobieństwo TAK / NIE
Wyszukiwarka
Podobne podstrony:
calki, WI ZUT studia, Metody numeryczne, od kolesia
MPiS wzory, WI ZUT studia, Metody probabilistyczne i statystyka, od kolesia
Metody optymalizacji, Księgozbiór, Studia, Metody numeryczne
Tematy2006, Studia, Metody numeryczne, Egzamin
symulacje numeryczne w pakiecie SCILAB SCICOS, Politechnika Lubelska, Studia, metody numeryczne
odp etyczna wobec klienta, Studia, Metodyka Pracy Socjalnej
więcej podobnych podstron