.::ZestaW IX::.

1. Rozwinąć w szereg potęgowy w otoczeniu x₀ funkcję f, jeżeli:

a)
, x₀=0 e)
, x₀=1

b)
, x₀=0 f)
, x₀=0

c)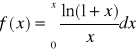
, x₀=0 g)
, x₀=-2

d)
, x₀=0 h)
, x₀=0

Korzystając z c) obliczyć przybliżoną wartość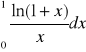
, z dokł. 0,01. Dla jakich x, f(x) jest równe sumie swojego rozwinięcia?

2. Rozwinąć w szereg trygonometryczny Fouriera funkcję:

a)
,

b)

c)

Narysować wykresy sum otrzymanych szeregów.

3. Rozwinąć w niepełne szeregi Fouriera funkcje:

a)

b)

Narysować wykresy sum otrzymanych szeregów, oraz obliczyć sumy

,
,
.

4. Rozwinąć w szereg cosinusów funkcję:

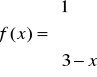
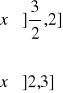
Narysować wykres sumy otrzymanego szeregu.